Problem K/C. 837. (December 2024)

K/C. 837. We have a \(\displaystyle 4\times 4\) table with a chessboard pattern. In a step we change the color of each square in a \(\displaystyle 2\times 2\) part of the table: black squares become white and white squares become black.

a) Is it possible to turn the whole table into black?

b) And if we start with a \(\displaystyle 5\times 5\) board, is it possible to turn the whole table into black?

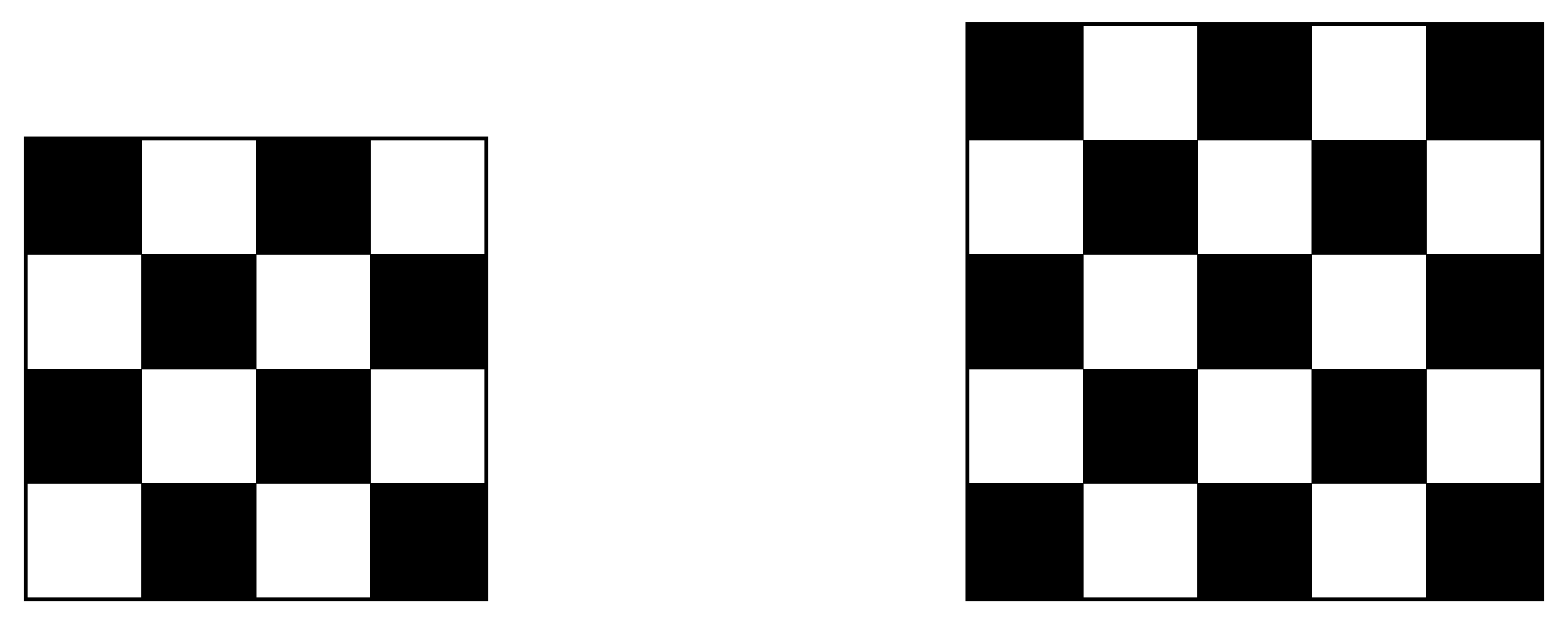
(5 pont)

Deadline expired on January 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. a) Igen, megoldható. Például így:

vagy például így:

b) Az \(\displaystyle 5\times5\)-ös táblázat minden egyes \(\displaystyle 2\times2\)-es mezőjén végrehajthatjuk az átszínezést, de ezek sorrendjétől nem függ a végső állás, mert minden mezőre csak a körülötte lévő \(\displaystyle 2\times2\)-es részek változtatása hat. Egy-egy ilyen \(\displaystyle 2\times2\)-es részt vagy átszínezünk valamikor, vagy nem. Ha páros sokszor színeztük, akkor az olyan, mintha nem színeztük volna, ha pedig páratlan sokszor, akkor az olyan, mintha csak egyszer színeztük volna. Így a 16 db \(\displaystyle 2\times2\)-es rész mindegyikén tulajdonképpen vagy változtatunk egyszer vagy nem. Tulajdonképpen csak azt kell eldönteni minden egyes \(\displaystyle 2\times\)2-es részről, hogy átszínezzük-e, vagy nem.

Mivel a sarokmezők a kiindulási helyzetben feketék, így a sarkokban lévő \(\displaystyle 2\times2\)-es részeket nem színezhetjük át, hiszen a sarokmezők színét csak ezek tudják megváltoztatni. Például a felső sor balról második mezője most fehér és azt csak a felső, balról második \(\displaystyle 2\times2\)-es mező átszínezésével tudjuk feketévé változtatni, de ekkor a harmadik mező fehér lesz, amit csakis a felső, balról harmadik \(\displaystyle 2\times2\)-es mező átszínezésével tudunk visszafeketíteni. Ugyanígy az alsó sorban.

Az eddigi átszínezések ,,kötelezőek" voltak, ha a csupa fekete táblát szeretnénk elérni, az alábbi álláshoz jutunk:

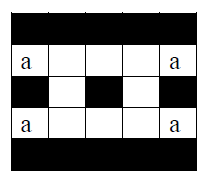
Most már csak a felső és alsó mezőket nem tartalmazó \(\displaystyle 2\times2\)-eseket színezhetjük át. Az a-val jelölt négy mezőt már csak egy-egy, őket tartalmazó (korábban nem átszínezett) \(\displaystyle 2\times2\)-es rész tartalmazza, így csakis ezek átszínezésével lehet őket feketévé változtatni, és ezt megtéve az alábbi színezést kapjuk:

Összesen négy \(\displaystyle 2\times2\)-es részt nem változtattunk meg, mégpedig azokat, melyek a táblázat középső mezőjét tartalmazzák. Ezek a középső \(\displaystyle 3\times3\)-as részen vannak. Ha bármelyiket átszínezzük, akkor ezzel együtt visszafehéredik egy-egy sarokmező ezen a \(\displaystyle 3\times3\)-as részen, melyek színén már változtatni a korábbiak alapján nem tudunk.

Így a teljesen fekete táblázatot elérni nem lehetséges.

Statistics:

210 students sent a solution.
5 points:	Abonyi Donát Tibor, Ali Rudolf, Bara Boglárka , Bense Tamás, Bodó Rókus Dániel, Csík Zoltán Richárd, Fejes-Tóth Fanni, Hajdu Vince, Hicsó Máté Kristóf, Kallós Klára, Kérdő Vilmos, Kudomrák Lili Anna , Lovas Márk, Majer Veronika, Maróti Olga, Mateas Isabelle, Mihály Attila, Miszori Márton, Molnár Levente, Nagypál Katóca, Németh Ábel, Papdi Benett, Patócs 420 Péter, Pázmándi Renáta , Péter Tamás, Radošická Emma, Rózsa Péter, Szabó Máté, Szekeres Anina, Timár Vince , Tóth Luca, Zsemlye Zsóka.
4 points:	28 students.
3 points:	47 students.
2 points:	58 students.
1 point:	8 students.
0 point:	9 students.
Unfair, not evaluated:	2 solutionss.
Not shown because of missing birth date or parental permission:	20 solutions.

Problems in Mathematics of KöMaL, December 2024