A K/C. 872. feladat (2025. október)

K/C. 872. Írjuk be az ábra \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle \ldots\), \(\displaystyle g\) betűvel jelölt tartományaiba az \(\displaystyle 1\), \(\displaystyle 2\), \(\displaystyle 3\), \(\displaystyle 4\), \(\displaystyle 5\), \(\displaystyle 6\) és \(\displaystyle 7\) számokat úgy, hogy a három körben a számok összege ugyanannyi, az \(\displaystyle a\) pedig négyszetszám legyen. Mennyi lehet ez az összeg? Keressük meg az összes megoldást.

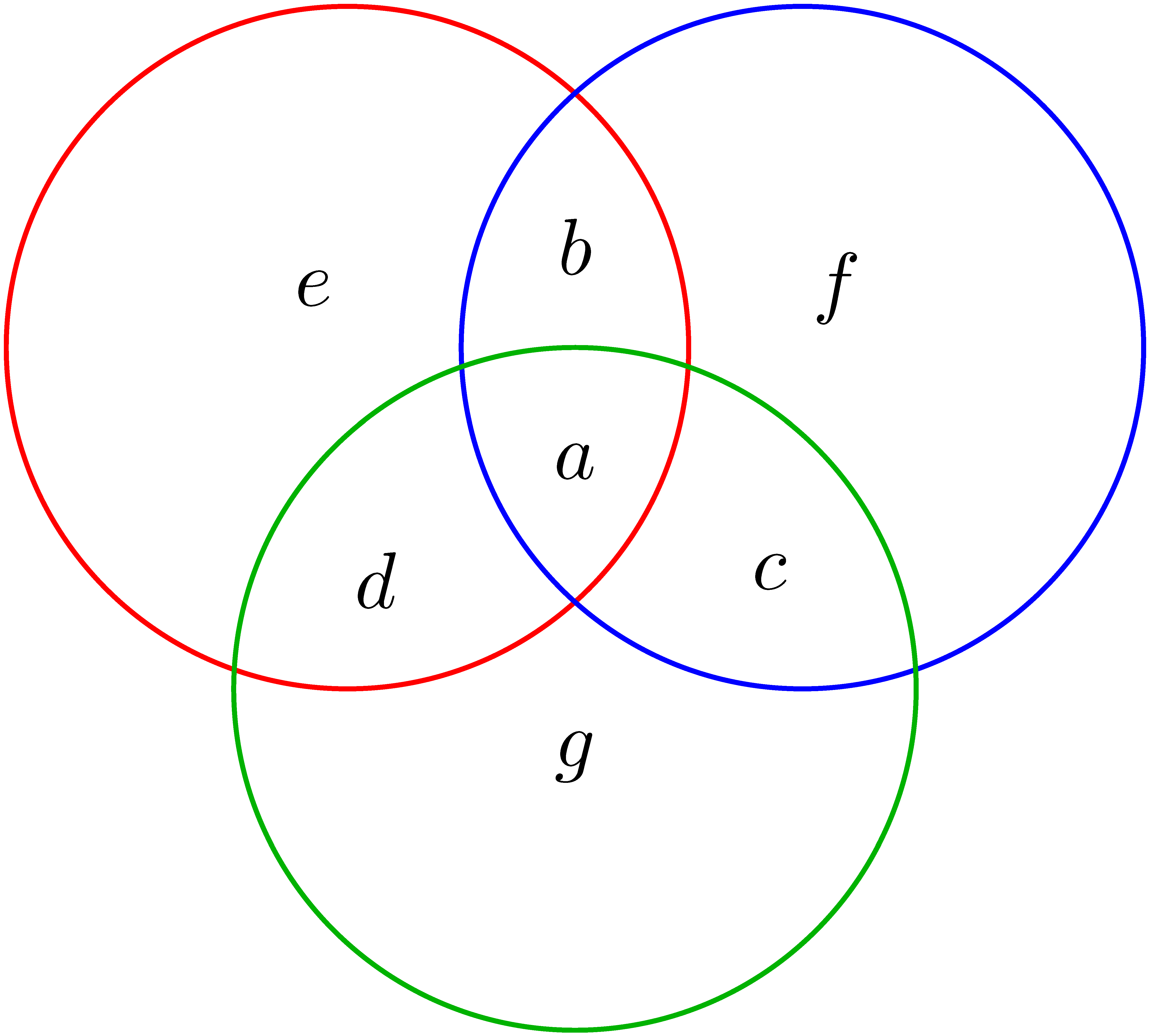
(5 pont)

A beküldési határidő 2025. november 10-én LEJÁRT.

Megoldás. A három körben a számok összege pontosan akkor ugyanannyi (bármely két kör közös számait is figyelembevéve), ha:

\(\displaystyle e+d = f+c,\)

\(\displaystyle b+f = d+g,\)

\(\displaystyle g+c = e+b.\)

Először legyen középen az 1, és legyen a 7 egy nem átfedett körrészben, pl. \(\displaystyle e=7\). Ekkor \(\displaystyle b=2\), \(\displaystyle 3\), \(\displaystyle 4\) lehet, mert \(\displaystyle b=5\), 6 esetén \(\displaystyle e+b\) túl nagy, amivel \(\displaystyle g+c\) nem lehet egyenlő. \(\displaystyle b=2\) esetén a maradék négy szám elhelyezésére – figyelembe véve a fenti egyenlőségeket – két elrendezés adódik. Ezeknél az összeg 13 és 14 lehet. \(\displaystyle b=3\), illetve \(\displaystyle b=4\) eset nem ad lényegesen eltérő új elrendezést.

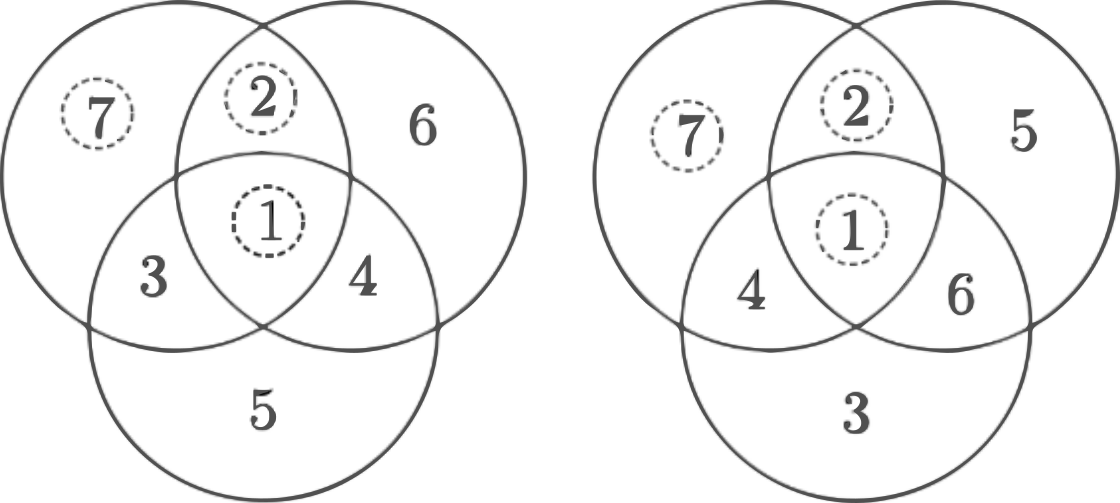
Legyen a 7-es egy két kör által lefedett részben, pl. \(\displaystyle b=7\). Ekkor \(\displaystyle e=5\) vagy 6 nem lehet, az \(\displaystyle e=2\), \(\displaystyle 3\), \(\displaystyle 4\) esetet megnézve két lényegesen különböző elrendezés adódik. Ezeknél az összeg 16 és 15 lehet.

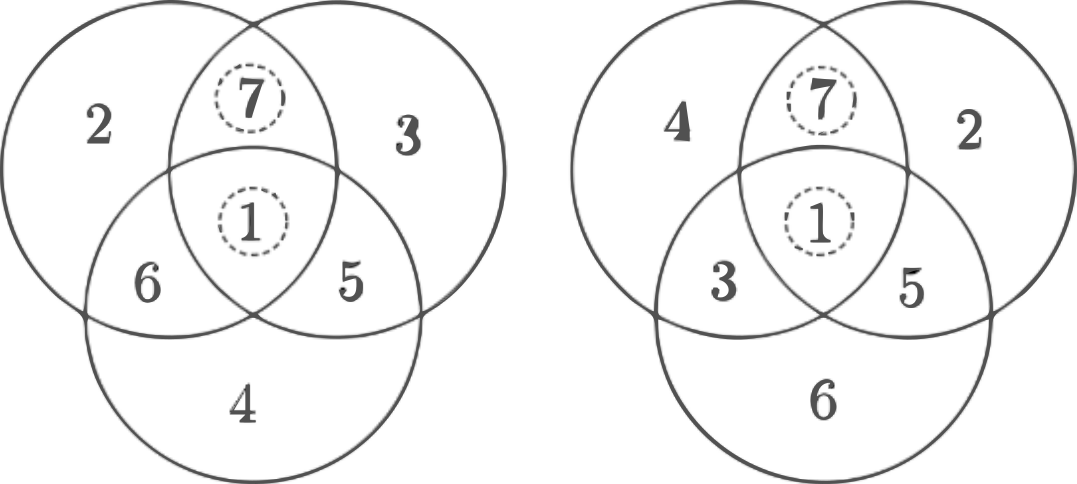
Ha a 4 van középen hasonlóképpen végignézve két különböző kitöltést kapunk, melyekben az összeg 14 és 18.

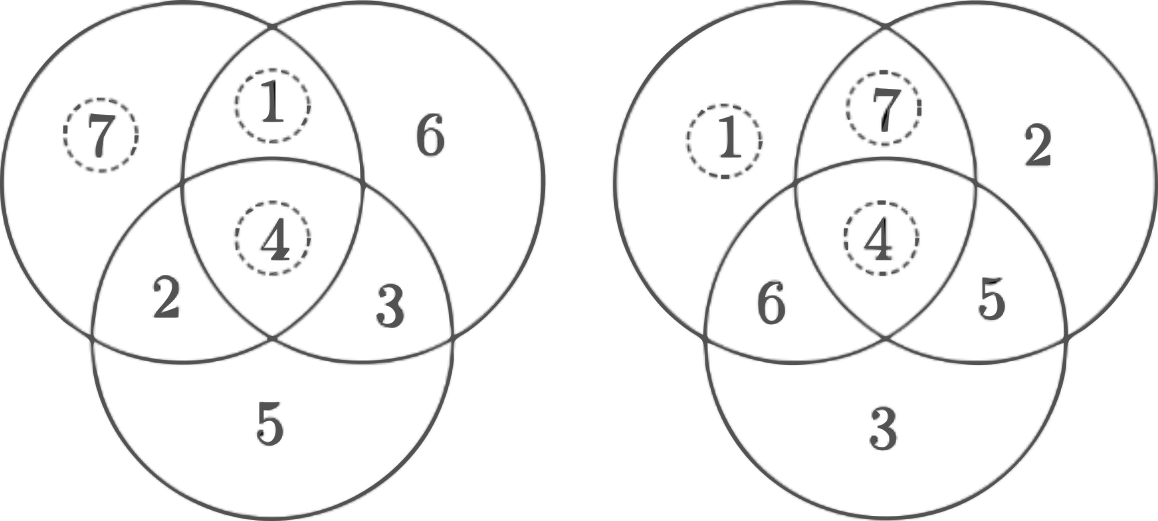
A keresett összeg 13, 14, 15, 16 és 18 lehet, és 6 különböző kitöltést találtunk.

Statisztika:

A K/C. 872. feladat értékelése még nem fejeződött be.

A KöMaL 2025. októberi matematika feladatai