 |
A K. 855. feladat (2025. április) |
K. 855. Három hajó egyszerre indult el egy kikötőből. Az egyik hajó északi, míg a másik kettő délkeleti irányba haladt, és mindhárom hajó pontosan egyszerre futott be a megfelelő kikötőbe. Ekkor az addig párban haladó két hajó szétvált, az egyik továbbment délkeleti irányba, a másik pedig az első megállójában veszteglő harmadik felé indult, és ez alkalommal is egyszerre kötöttek ki. Az északi irányhoz képest mekkora szögben kellett ezután a két azonos helyen lévő hajónak elindulnia, hogy nyílegyenesen abba a kikötőbe érkezzen, ahol az előzőleg végig délkelet felé haladó hajó várakozott? (Minden szakaszon minden hajónak ugyanakkora volt az átlagsebessége.)
Javasolta: Kozma Katalin Abigél (Győr)
(5 pont)
A beküldési határidő 2025. május 12-én LEJÁRT.
Megoldás. Készítsünk ábrát a szöveg alapján! A hajók a \(\displaystyle K\) pontból indulnak, az északi kikötő helyét \(\displaystyle L\), a délkeleti irányban lévő kikötők helyét \(\displaystyle M\), illetve \(\displaystyle N\) pont jelöli. Feladatunk, hogy az ábrán \(\displaystyle \varphi\)-vel jelölt \(\displaystyle NLK \sphericalangle\) szög nagyságát meghatározzuk.
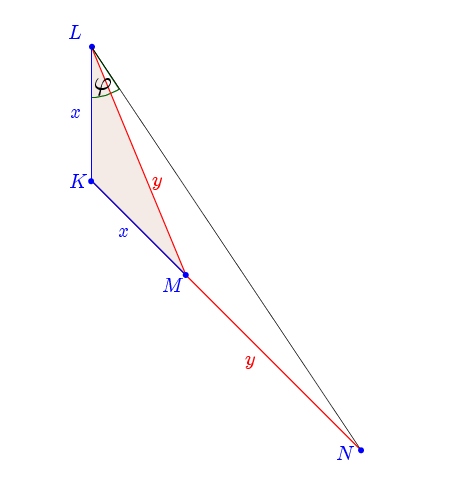
Ekkor az északi és a délkeleti irány miatt \(\displaystyle LKM \sphericalangle=135^\text{\(\displaystyle \circ\)}.\) Az egy időben való érkezés és az azonos átlagsebesség miatt \(\displaystyle KL=KM\), illetve \(\displaystyle ML=MN\), ezen szakaszok hosszát \(\displaystyle x\)-szel, illetve \(\displaystyle y\)-nal jelöltük. Nyilvánvaló, hogy az \(\displaystyle LKM\) és az \(\displaystyle LMN\) háromszög is egyenlő szárú. Először az \(\displaystyle LKM\) háromszög alapon fekvő szögeit tudjuk kiszámolni:
\(\displaystyle MLK \sphericalangle=KML \sphericalangle=\frac{180^\text{\(\displaystyle \circ\)}-135^\text{\(\displaystyle \circ\)}}{2}=22,\!5^\text{\(\displaystyle \circ\)}.\)
A \(\displaystyle KML\sphericalangle\) külső szöge az \(\displaystyle LMN\) háromszögnek, így nagysága egyenlő a nem mellette fekvő két belső szög összegével, ezért
\(\displaystyle NLM \sphericalangle=MNL \sphericalangle=\frac{22,\!5^\text{\(\displaystyle \circ\)}}{2}=11,\!25^\text{\(\displaystyle \circ\)}.\)
A \(\displaystyle \varphi\) szög az \(\displaystyle MLK \sphericalangle\) és az \(\displaystyle NLM \sphericalangle\) összege, így a keresett szög mértéke:
\(\displaystyle \varphi=22,\!5^\text{\(\displaystyle \circ\)}+11,\!25^\text{\(\displaystyle \circ\)}=33,\!75^\text{\(\displaystyle \circ\)}.\)
A két hajó az északi irányhoz, tehát a \(\displaystyle \overrightarrow{KL}\) vektor irányához képest az \(\displaystyle \overrightarrow{LN}\) irányban halad az \(\displaystyle N\) kikötő felé, a két vektor irányának bezárt szöge \(\displaystyle 180^{\circ}-33,75^{\circ}=146,25^{\circ}\), ezért az északi irányhoz képest \(\displaystyle 146,25^{\circ}\)-os szögben kell elindulniuk.
Statisztika:
A KöMaL 2025. áprilisi matematika feladatai
