A K. 860. feladat (2025. május)

K. 860. Anna és Boglárka egy másfél méter átmérőjű kör alakú étkezőasztalnál játszik. Anna leteszi az asztalra a \(\displaystyle 42\times30~\mathrm{cm}\)-es téglalap alakú papírlapját, Boglárka pedig rárakja az ugyanekkora lapját úgy, hogy a két lap egy-egy átlója pontosan illeszkedik egymásra, ám a lapok nem fedik teljes egészében egymást és nem lógnak le az asztalról. Az asztallap hány százalékát fedi le így a két lap?

Javasolta: Kozma Katalin Abigél (Győr)

(5 pont)

A beküldési határidő 2025. június 10-én LEJÁRT.

Megoldás. Készítsünk ábrát és használjuk a jelöléseit! A feladat feltételei alapján \(\displaystyle AB=EC=30\) cm, valamint \(\displaystyle BC=AE=40\) cm.

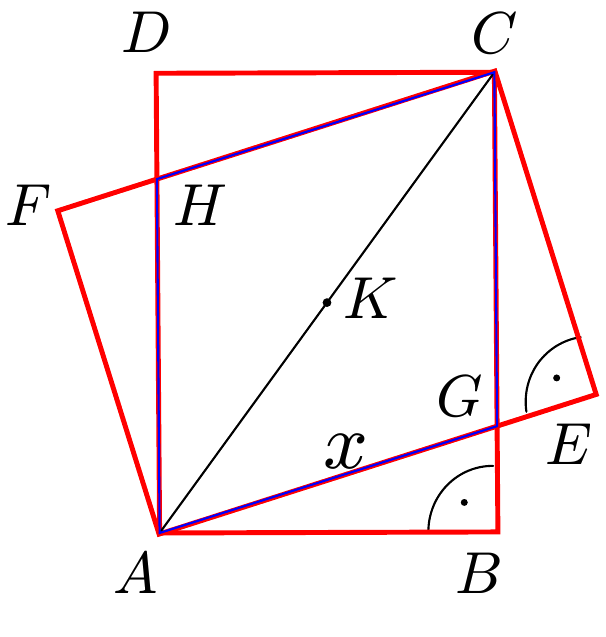
Először belátjuk, hogy a két téglalap közös része, azaz az \(\displaystyle AGCH\) négyszög rombusz. Legyen \(\displaystyle K\) a két téglalap közös \(\displaystyle AC\) átlójának felezőpontja, ekkor \(\displaystyle K\) mindkét téglalap szimmetriaközéppontja, így az \(\displaystyle AGCH\) négyszögnek is, azaz az \(\displaystyle AGCH\) négyszög paralelogramma. Most már csak azt kell megmutatnunk, hogy két szomszédos oldalának hossza egyenlő. Tekintsük az \(\displaystyle ABG\) és a \(\displaystyle GEC\) derékszögű háromszöget. Mivel a \(\displaystyle G\) csúcsnál fekvő \(\displaystyle BGA\) és \(\displaystyle CGE\) szögek csúcsszögek, ezért egyenlők, így a két háromszög belsői szögei ugyanakkorák, azaz hasonlók. Sőt, egybevágóak is, hiszen \(\displaystyle AB=EC\), azaz a megfelelő befogójuk ugyanakkora. Emiatt az átfogójuk is ugyanakkora, azaz \(\displaystyle CG=AG=x\), így beláttuk, hogy az \(\displaystyle AGCH\) négyszög rombusz. Második lépésben kiszámítjuk a rombusz területét, ehhez először meghatározzuk \(\displaystyle x\)-et. Adott, hogy \(\displaystyle BC=42\) és \(\displaystyle CG=x\), ezért \(\displaystyle BG=42-x\). Alkalmazzuk Pitagorasz tételét az \(\displaystyle ABG\) háromszögben:

\(\displaystyle AB^2+BG^2=AG^2,\)

\(\displaystyle 30^2+(42-x)^2=x^2,\)

\(\displaystyle 900+1764-84x+x^2=x^2,\)

amiből \(\displaystyle x=\frac{222}{7} \approx 31,\!71\) cm. Az \(\displaystyle AGCH\) rombusz területe:

\(\displaystyle T=30 \cdot x=\frac{6660}{7}\approx 951,\!43~ \text{cm}^2. \)

Ekkor a papírlapok által lefedett terület:

\(\displaystyle 2 \cdot (30 \cdot 42)-\frac{6660}{7}=\frac{10980}{7}\approx 1568,\!57 ~ \text{cm}^2.\)

Az asztallap területe: \(\displaystyle T_{\text{kör}}=75^2 \pi=5625\pi\approx 17671,\!46 ~ \text{cm}^2,\) ebből a keresett arány:

\(\displaystyle \frac{\frac{10980}{7}}{5625\pi}=\frac{244}{875\pi}\approx 0,\!0888,\)

vagyis az asztal területének \(\displaystyle 8,\!88\%\)-át fedi le a két, egymásra rakott papírlap.

Statisztika:

54 dolgozat érkezett.
5 pontot kapott:	Bloemsma Péter Sándor, Csík Zoltán Richárd, Fórján Bernát, Hajdu Vince, Holló Barnabás, Izsa Ferenc Gergő, Jancsurák Flóra, Kalapos Szonja, Kása Richárd Zsolt, Kiss Ákos, Kovács Domonkos, Laczó Zoltán, Lovas Márk, Macskássy Márk, Makra Zóra Liliána, Mátyás Levente, Medgyesi András, Molnár Levente, Nagy Alexander, Péter Tamás, Radošická Emma, Rózsa Péter, Szabó Flóra, Szighardt Anna, Zsilák Márk Péter.
4 pontot kapott:	Csató Németh-Meskó, Győrffy Csanád, Kudomrák Lili Anna , Kun Milán, Majer Veronika, Patócs 420 Péter, Silye Zalán, Szabó Anita.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	10 versenyző.
0 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	4 dolgozat.

A KöMaL 2025. májusi matematika feladatai