A K. 864. feladat (2025. szeptember)

K. 864. Az alábbi elrendezést gyufákból készítettük. Legkevesebb hány gyufát kell áthelyeznünk ahhoz, hogy az öt egybevágó négyzet helyett csak négy, az eredetiekkel egybevágó legyen látható az új elrendezésben? (A négyzetlapok nem fedhetik át egymást, csak oldaluk vagy csúcsuk lehet közös, és befejezetlen négyzetet sem alakíthatunk ki.)

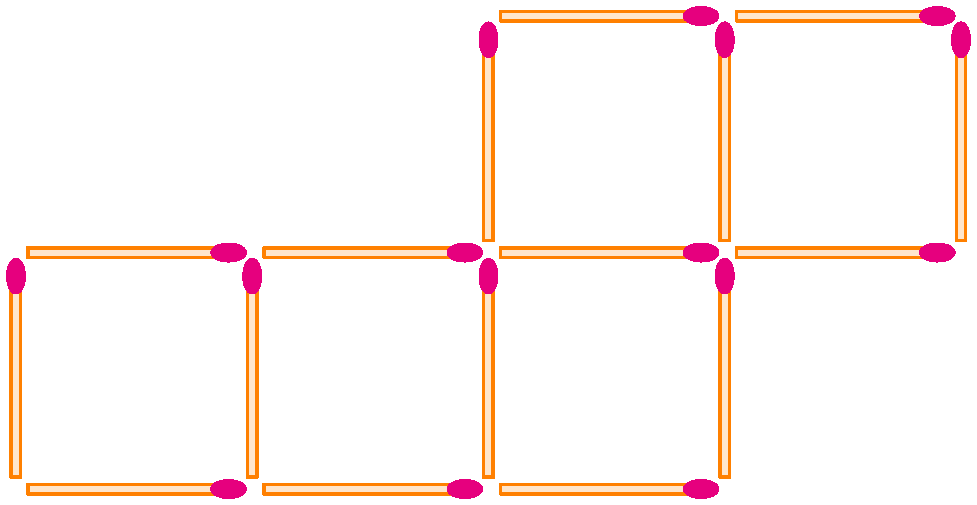
(5 pont)

A beküldési határidő 2025. október 10-én LEJÁRT.

Megoldás. Mivel 16 gyufa van, és négy négyzetet kell létrehoznunk, ezért semelyik két négyzetnek nem lehet közös oldala az új elrendezésben. Ezt két gyufa áthelyezésével el tudjuk érni (lásd ábra).

Egy gyufa áthelyezése esetén vagy az A és B, vagy a C és D négyzetek megmaradnak, ezért lesz két egymáshoz csatlakozó oldalú négyzet, így nem hozható létre négy különálló négyzet.

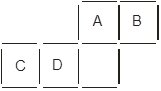
Statisztika:

185 dolgozat érkezett.
5 pontot kapott:	Adamcsek Ágnes, Balogh Fülöp, Csikós Attila, Csutak András, Fekete Rebeka Katica, Hruby Olivér, Kelepecz Kornél Zoltán, Körmöndi Csanád, Lajkó Linda, Laukó Zalán, Palik Ábris Csanád, Schneider Viola, Solymosi Molnár Dóra, Szabó Zoárd, Török Ákos, Varga 343 Bálint, Varga011Hajnalka, Verebély Nadin.
4 pontot kapott:	Bachesz Kende, Biró Beáta , Buliczka Csombor, Csuvár Barnabás, Gazsi Levente, Hajnal Kamilla, Harcsa-Czenke István, Kis Ágota , Kőrös Anna, Oros Áron, Papp Dénes, Tasnádi Bendegúz, Tőkés Huba , Ványi Nándor.
3 pontot kapott:	34 versenyző.
2 pontot kapott:	47 versenyző.
1 pontot kapott:	20 versenyző.
0 pontot kapott:	34 versenyző.
Nem versenyszerű:	3 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	15 dolgozat.

A KöMaL 2025. szeptemberi matematika feladatai