 |
Az M. 438. feladat (2025. február) |
M. 438. Adott számú dominót állítsunk fel egy egyenes mentén, egymástól azonos távolságra, majd lökjük meg az első dominót. Mennyi idővel később dől el az utolsó dominó? Hogyan függ ez az idő a dominók közötti távolságtól?
Közli: Széchenyi Gábor, Budapest
(6 pont)
A beküldési határidő 2025. március 17-én LEJÁRT.
Megoldás. Körülbelül \(\displaystyle 1{,}5~\mathrm{m}\) hosszúra kihúztam a mérőszalagot, majd egy sima felületre, a padlóra ragasztószalaggal rögzítettem a két végét. Ennek a segítségével felállítottam a dominókat egymástól egyenlő távolságra (1. ábra). A dominók száma minden esetben 28 volt. Ezután okostelefon segítséggel elkészítettem a felvételeket. Mindegyik távolsággal háromszor végeztem el a mérést. A mozgás rögzítéséhez 240 képkocka/másodperc fényképezési frekvenciát választottam, ami körülbelül \(\displaystyle 4{,}2~\mathrm{ms}\) időbeli felbontást tett lehetővé. A felvételeket ezután a VLC alkalmazással elemeztem. Az alkalmazás kiválasztásánál fontos szempont volt, hogy azzal a felvétel képkockái egyenként megnézhetőek legyenek, ezért a VLC alkalmazáshoz letöltöttem a Time v3.2 nevű bővítményt, ami ezt lehetővé tette (2. ábra). A felvételekből ilyen módon meghatároztam azt, hogy a második és az utolsó dominó mikor kezdett el dőlni. Azért a másodikat vettem és nem az elsőt, mert az első dőlési idejét (amíg eléri a következő dominót) erősebben befolyásolja az, hogy mennyire erősen löktem meg.

1. ábra

2. ábra
A két idő különbségéből kaptam a dominósor vizsgált részének \(\displaystyle \Delta t\) eldőlési idejét. Az így kapott értékeket a dominók közötti \(\displaystyle d\) távolság függvényében ábrázoltam (3. ábra).
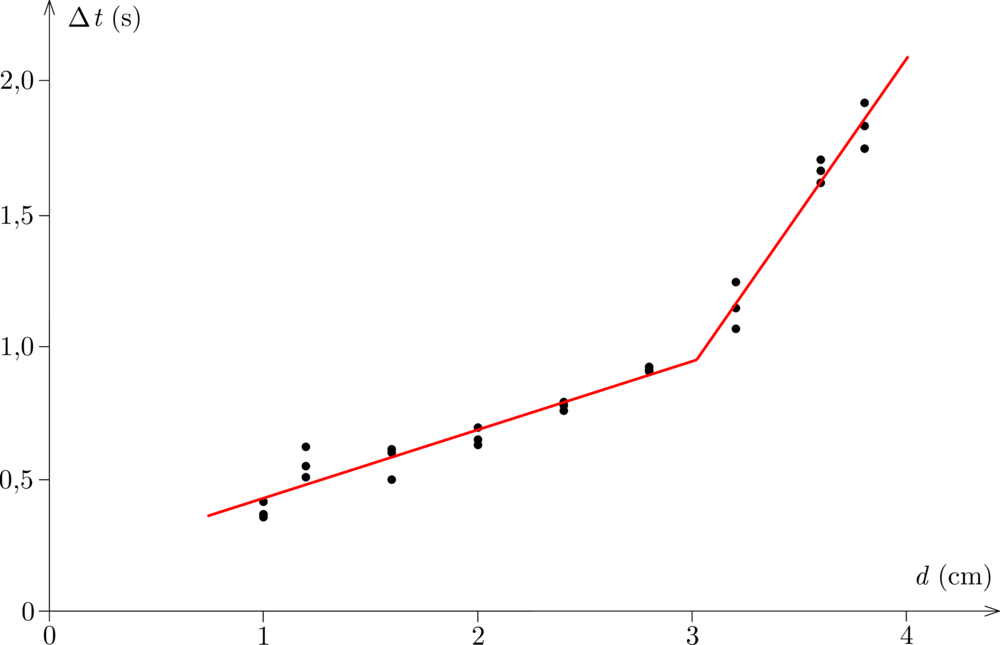
3. ábra
A grafikonon jól látható, hogy a teljes dominósor eldőlési ideje nem arányos a dominók közötti távolsággal, és így a dominósor teljes hosszával. Mivel a teljes dominó sor hossza a dominók közötti távolsággal arányos, ezért a dőlési front haladási sebessége függ a dominók távolságától. Kisebb dominók közötti távolságnál ez a sebesség nagyobb, mint nagyobb távolságoknál. A mérési pontokat két részre osztottam a kisebb, illetve a nagyobb távolságok szerint. Ezekre a csoportokra külön-külön egy-egy egyenest illesztettem. Az egyenesek meredekségeiből megbecsültem a dőlési front terjedési sebességét. Kis (kb. 3 cm-nél kisebb) dominóközök esetén a dőlési front terjedési sebessége
\(\displaystyle v_1=(101\pm 9)~\mathrm{cm}/\mathrm{s}, \)
és nagy (3 cm-nél nagyobb) dominóközök esetén
\(\displaystyle v_2=(22{,}5\pm 1{,}5)~\mathrm{cm}/\mathrm{s}. \)
Előbbi körülbelül \(\displaystyle 4{,}5\)-szer nagyobb, mint az utóbbi.
Az időpontok leolvasási hibája körülbelül a képkockák közötti idővel becsülhető, ami \(\displaystyle \pm 2{,}1~\mathrm{ms}\). Kisebb értékű hibát eredményezhet a dominók közötti távolság pontatlansága, ami körülbelül \(\displaystyle \pm 0{,}25~\mathrm{mm}\). A dominók párhuzamossága sem volt tökéletes, ami szintén befolyásolhatta az időket.
Fülöp Magdaléna (Pécsi Leőwey Klára Gimn., 10. évf.)
Statisztika:
11 dolgozat érkezett. 6 pontot kapott: Fülöp Magdaléna. 5 pontot kapott: Gáti Benjamin, Hegedüs Márk, Szabadkai Ferenc, Szőke Bottyán. 4 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2025. februári fizika feladatai

