Problem P. 5047. (September 2018)

P. 5047. The cart of mass \(\displaystyle M\) and the flat block of mass \(\displaystyle m\) on the cart are moving at a speed of \(\displaystyle v\) towards a compression spring fixed to a wall, and having a spring constant of \(\displaystyle D\). The coefficient of friction between the block and the cart is \(\displaystyle \mu\). \(\displaystyle a)\) Will the block slip or not when the collision occurs? \(\displaystyle b)\) How long does the collision last? Data: \(\displaystyle M=0.2\) kg, \(\displaystyle m=0.1\) kg, \(\displaystyle v=1\) m/s, \(\displaystyle D=4.4\) N/m, \(\displaystyle \mu=0.4\).

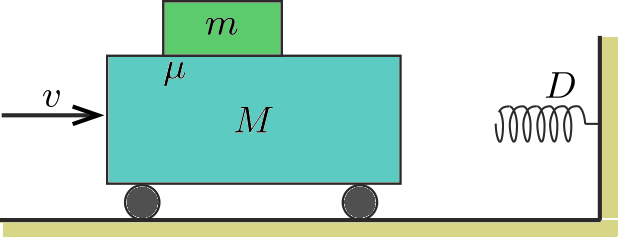
(4 pont)

Deadline expired on October 10, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A rugóhoz nyomódó kiskocsi egy harmonikus rezgőmozgás fél periódusát teszi meg. A körfrekvencia:

\(\displaystyle \omega=\sqrt{\frac{D}{m+M}}=3{,}83~\rm s^{-1}.\)

Az \(\displaystyle A\) amplitúdójú rezgőmozgás kezdeti sebessége \(\displaystyle v=A\omega\), ahonnan

\(\displaystyle A=\frac{v}{\omega}=\frac{1}{3{,}83}\,{\rm m}\approx 26~\rm cm.\)

\(\displaystyle a)\) A kiskocsi és a rajta lévő hasáb maximális gyorsulása (ha a hasáb nem csúszik meg):

\(\displaystyle a_\text{max}=A\omega^2=v\omega=3{,}8~{\rm m/s}^2.\)

Ekkora gyorsulást a súrlódási erő akkor tud létrehozni, ha

\(\displaystyle a_\text{max}<\mu g\approx 3{,}9~{\rm m/s}^2.\)

Ez valóban fennáll, tehát a hasáb nem csúszik meg a kiskocsin.

\(\displaystyle b)\) Az ütközés ideje a teljes rezgésidő fele:

\(\displaystyle \Delta T=\frac{T}{2}=\frac{\pi}{\omega}=0{,}82~\rm s.\)

Statistics:

98 students sent a solution.
4 points:	Bekes Barnabás, Békési Ábel, Bokor Endre, Bonifert Balázs, Csépányi István, Debreczeni Tibor, Fekete András Albert, Fekete Levente, Fiam Regina, Fonyi Máté Sándor, Fülöp Sámuel Sihombing, Garamvölgyi István Attila, Gulácsi Máté, Györgyfalvai Fanni, Jánosdeák Márk, Kertész Balázs, Köpenczei Csenge, Laposa Hédi, Mácsai Dániel, Marozsák Tádé, Máth Benedek, Molnár Mátyás, Németh Kristóf, Olosz Adél, Rusvai Miklós, Sas 202 Mór, Schneider Anna, Stefán Boglárka Abigél, Sugár Soma, Sümegi Géza, Szoboszlai Szilveszter, Tafferner Zoltán, Takács Árpád, Tiefenbeck Flórián, Vaszary Tamás, Virág Levente.
3 points:	23 students.
2 points:	10 students.
1 point:	25 students.
0 point:	2 students.
Not shown because of missing birth date or parental permission:	2 solutions.

Problems in Physics of KöMaL, September 2018