A P. 5068. feladat (2018. november)

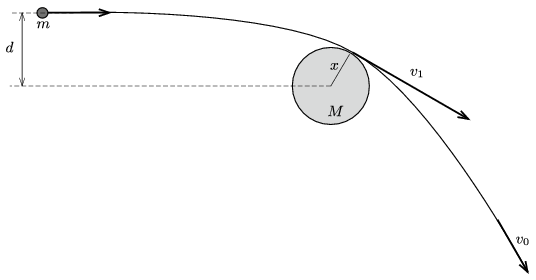
P. 5068. Egy kicsiny, pontszerűnek tekinthető, \(\displaystyle m\) tömegű üstökös közeledik egy \(\displaystyle M\) tömegű, \(\displaystyle R\) sugarú, gömb alakú bolygó felé (\(\displaystyle m\ll M\)). Az üstökös sebessége a bolygótól nagyon messze \(\displaystyle v_0\), és ha nem hatna rá a bolygó gravitációs tere, akkor \(\displaystyle d\) távolságra haladna el a bolygó középpontjától (\(\displaystyle d>R\)). Mekkora \(\displaystyle v_0\) minimális értéke, amelynél az üstökös még nem ütközik a bolygóba? (A bolygón és az üstökösön kívül minden más égitest gravitációs hatását elhanyagolhatjuk.)

Közli: Kovács József, Szombathely

(5 pont)

A beküldési határidő 2018. december 10-én LEJÁRT.

Megoldás. Jelöljük az üstökös maximális sebességét \(\displaystyle v_1\)-gyel, a bolygó középpontjától mért legkisebb távolságát pedig \(\displaystyle x\)-szel. A perdületmegmaradás törvénye szerint

\(\displaystyle mv_0d=mv_1x,\)

az energiamegmaradás törvénye pedig így alkalmazható:

\(\displaystyle \frac{1}{2}mv_0^2=\frac{1}{2}mv_1^2-\gamma\frac{mM}{x}.\)

A fenti két egyenletből (\(\displaystyle v_1\) kiküszöbölése után)

\(\displaystyle x^2+2\frac{\gamma M}{v_0^2}x-d^2=0\)

adódik, amelynek (pozitív) megoldása:

\(\displaystyle x=\sqrt{ \left(\frac{\gamma M}{v_0^2}\right)^2+d^2}-\frac{\gamma M}{v_0^2}. \)

Az üstökös akkor nem ütközik a bolygóval, ha \(\displaystyle x>R\), vagyis

\(\displaystyle \sqrt{ \left(\frac{\gamma M}{v_0^2}\right)^2+d^2}-\frac{\gamma M}{v_0^2}>R,\)

azaz

\(\displaystyle \left(\frac{\gamma M}{v_0^2}\right)^2+d^2>\left(\frac{\gamma M}{v_0^2}+R\right)^2,\)

\(\displaystyle d^2-R^2>\frac{2\gamma M R}{v_0^2},\)

tehát

\(\displaystyle v_0>\sqrt{\frac{2\gamma MR}{d^2-R^2}} .\)

Statisztika:

40 dolgozat érkezett.
5 pontot kapott:	Békési Ábel, Bokor Endre, Bonifert Balázs, Csépányi István, Elek Péter, Forgács Kata, Fülöp Sámuel Sihombing, Kárpáti Kristóf, Kertész Balázs, Kozák 023 Áron, Lipták Gergő, Mácsai Dániel, Makovsky Mihály, Marozsák Tádé, Máth Benedek, Merkl Gergely, Merkl Levente, Molnár Mátyás, Morvai Orsolya, Olosz Adél, Sal Dávid, Simon Tamás, Székely Bálint, Szoboszlai Szilveszter, Tiefenbeck Flórián, Toronyi András, Turcsányi Máté, Varga Vázsony, Vaszary Tamás, Viczián Anna.
4 pontot kapott:	Bukor Benedek.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	5 versenyző.

A KöMaL 2018. novemberi fizika feladatai