A P. 5180. feladat (2019. december)

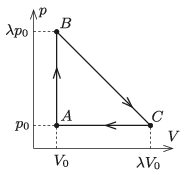
P. 5180. Egyatomos ideális gáz az ábrán látható \(\displaystyle ABCA\) körfolyamatot végzi. Mekkora a körfolyamat hatásfoka, ha a gáz (kelvinben mért) legmagasabb hőmérséklete kilencszer akkora, mint a legalacsonyabb hőmérséklet?

(Lásd még Gálfi László: Hőfelvétel vagy hőleadás? című cikket a KöMaL 2009. évi 4. számában vagy a honlapunkon!)

Közli: Dezsőfi György, Miskolc

(5 pont)

A beküldési határidő 2020. január 10-én LEJÁRT.

Megoldás. Először határozzuk meg \(\displaystyle \lambda\) értékét! Az 1. ábrán feltüntettük a legalacsonyabb és a legmagasabb hőmérséklethez tartozó izotermákat. Az állapotegyenlet szerint

\(\displaystyle T=\frac{pV}{nR},\)

vagyis az izotermák a \(\displaystyle pV=\)állandó egyenletű hiperbolák.

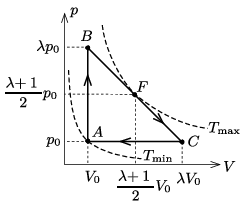
1. ábra

A körfolyamatban a legalacsonyabb hőmérséklet az \(\displaystyle A\) ponthoz tartozik:

\(\displaystyle T_\text{min}=\frac{p_0V_0}{nR}.\)

A legmagasabb hőmérsékletű állapotot ott találjuk, ahol az izoterma érinti a \(\displaystyle BC\) egyenest. Ez az ábra szimmetrikus volta miatt a \(\displaystyle BC\) szakasz \(\displaystyle F\) felezőpontjában teljesül, és ott

\(\displaystyle T_\text{max}= \left(\frac{\lambda+1}{2}\right)^2\frac{p_0V_0}{nR}.\)

Látható, hogy a megadott \(\displaystyle T_\text{max}=9T_\text{min}\) feltétel akkor áll fenn, ha \(\displaystyle \lambda=5\).

A gáz által végzett ,,hasznos'' munka az\(\displaystyle ABC\) háromszög területe:

\(\displaystyle W=\frac{(4p_0\cdot 4V_0)}{2}= 8\,p_0V_0.\)

A hatásfok kiszámításához meg kell határoznunk a körfolyamat során felvett hőt. A \(\displaystyle C\rightarrow A\) szakaszon (izobár összehúzódás) hőleadás történik. Az \(\displaystyle A\rightarrow B\) szakaszon (izochor állapotváltozás) tágulási munka nincs, a hőfelvétel a belső energia növekedésével egyezik meg:

\(\displaystyle Q_{AB}=E_B-E_A=\frac{3}{2}(\lambda-1)p_0V_0=6\,p_0V_0.\)

(Felhasználtuk, hogy az egyatomos ideális gáz belső energiája \(\displaystyle E=\tfrac32 pV\).)

Bonyolultabb a helyzet a \(\displaystyle B\rightarrow C\) szakaszon történő hőfelvétellel. A folyamat elején, a 2. ábrán bejelölt \(\displaystyle D\) pontig hőfelvétel, \(\displaystyle D\) és \(\displaystyle C\) között pedig hőleadás történik.

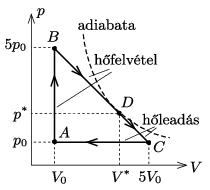
2. ábra

A \(\displaystyle D\) pontot az jellemzi, hogy a rajta átmenő adiabata érinti a \(\displaystyle BC\) egyenest, vagyis a \(\displaystyle D\) pont környékén egy kicsi \(\displaystyle \Delta V\) térfogatváltozásnál nincs hőcsere, a belső energia csökkenése éppen fedezi a gáz által végzett tágulási munkát:

\(\displaystyle \frac{3}{2}\left(p^*-\frac{p_0}{V_0}\Delta V\right)( V^*+\Delta V)-\frac{3}{2}p^* V_D+p_D\Delta V=0. \)

(Felhasználtuk, hogy a \(\displaystyle BC\) egyenes mentén \(\displaystyle \Delta p=-(p_0/V_0)\Delta V.\)) A fenti egyenletből a \(\displaystyle (\Delta V)^2\)-tel arányos (másodrendűen kicsiny) tagot elhagyva

\(\displaystyle \frac{p^*}{V^*}=\frac{3}{5}\,\frac{p_0}{V_0}\)

következik. Másrészt tudjuk, hogy \(\displaystyle D\) rajta fekszik a \(\displaystyle BC\) egyenesen, vagyis

\(\displaystyle \frac{p^*}{p_0}=6-\frac{V^*}{V_0}.\)

Ebből a két összefüggésből kifejezhetjük a hőfelvétel határának állapotjelzőit:

\(\displaystyle V^*=\frac{15}{4}V_0 \qquad \text{és} \qquad p^*=\frac{9}{4}p_0.\)

Most már nincs akadálya annak, hogy megadjuk a \(\displaystyle B\rightarrow D\) folyamat alatt felvett hő nagyságát:

\(\displaystyle Q_{BD}=E_D-E_B+W'_{B\rightarrow D}=\frac32(p^*V^*-p_0V_0)+\frac{5p_0+p^*}{2}(V^*-V_0)=\frac{121}{8}p_0V_0\approx 15{,}1p_0V_0. \)

A teljes hőfelvétel a körfolyamatban:

\(\displaystyle Q^{\rm fel}_\text{összes}= Q_{AB}+Q_{BD}=\frac{169}{8}\approx 21{,}1p_0V_0, \)

és végül a körfolyamat termikus hatásfoka:

\(\displaystyle \eta=\frac{W}{Q^{\rm fel}_\text{összes}}=\frac{64}{169}\approx 0{,}38=38\%.\)

Statisztika:

31 dolgozat érkezett.
5 pontot kapott:	Bokor Endre, Bonifert Balázs, Fekete András Albert, Horváth 999 Anikó, Ludányi Levente, Nguyễn Đức Anh Quân, Somlán Gellért, Téglás Panna, Toronyi András, Tóth Ábel, Vass Bence.
4 pontot kapott:	Fekete Levente.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	11 versenyző.

A KöMaL 2019. decemberi fizika feladatai