 |
A P. 5183. feladat (2019. december) |
P. 5183. Az ábrán látható függőleges sínpár felső végét \(\displaystyle L\) induktivitású tekerccsel zártuk. A sínek távolsága \(\displaystyle \ell\), rajtuk súrlódásmentesen mozoghat egy \(\displaystyle m\) tömegű, elhanyagolható ellenállású rúd. A külső mágneses tér \(\displaystyle \boldsymbol B\) indukcióvektora vízszintes és merőleges a sínek síkjára.
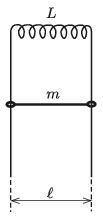
A rudat elengedve
\(\displaystyle a)\) legfeljebb mekkora feszültség indukálódik a tekercsben;
\(\displaystyle b)\) legfeljebb mekkora lesz az indukált áram erőssége?
Varga István (1952–2007) feladata
(5 pont)
A beküldési határidő 2020. január 10-én LEJÁRT.
Megoldás. Jelöljük a rúd pillanatnyi elmozdulását \(\displaystyle x(t)\)-vel, az áramerősséget \(\displaystyle I(t)\)-vel, és a tekercs végpontjai közötti feszültséget \(\displaystyle U(t)\)-vel! A gravitációs helyzeti energia csökkenése megegyezik a rúd mozgási energiájának és a tekercs mágneses energiájának növekedtével:
| \(\displaystyle (1)\) | \(\displaystyle mgx(t)=\frac{L}{2}I(t)^2+\frac{m}{2}v(t)^2.\) |
Igaz továbbá, hogy a rúdban indukálódó \(\displaystyle U(t)=B\ell v(t)\) feszültség a tekercs végpontjai közötti feszültség ugyanakkora:
\(\displaystyle B\ell v(t)=L\frac{\Delta I(t)}{\Delta t},\)
amit \(\displaystyle v(t)=\frac{\Delta x(t)}{\Delta t}\) miatt így is felírhatunk:
\(\displaystyle \frac{\Delta (LI -B\ell x)}{\Delta t}= 0, \qquad \text{azaz} \qquad LI(t)-B\ell x(t)=\text{állandó}.\)
Az állandó értéke nulla, hiszen a rúd elengedésekor \(\displaystyle I(0)=v(0)=0.\) Látjuk tehát, hogy az áramkör áramerőssége arányos a rúd elmozdulásával (süllyedésével):
| \(\displaystyle (2)\) | \(\displaystyle I(t)=\frac{B\ell}{L}\, x(t).\) |
Ezt visszaírva (1)-be a
| \(\displaystyle (3)\) | \(\displaystyle v^2=2gx-\frac{B^2\ell^2}{mL}\,x^2\) |
kvadratikus kifejezést kapjuk. Ebből leolvasható, hogy a rúd legnagyobb elmozdulása (ahol a sebesség ismét nullává válik):
\(\displaystyle x_\text{max}=\frac{2mgL}{B^2\ell^2}.\)
Az áramerősség legnagyobb értékét a legnagyobb elmozdulásból (2) alapján számíthatjuk ki:
\(\displaystyle I_\text{max}=\frac{2mg}{B\ell}.\)
A rúd legnagyobb sebessége a (3) kvadratikus kifejezés maximális értéke:
\(\displaystyle v_\text{max}=\frac{g}{B \ell }\sqrt{mL}.\)
(Ezt \(\displaystyle v(x)\) teljes négyzetté alakításával vagy szélsőérték-számítással, esetleg a parabola tulajdonságainak kihasználásával láthatjuk be.) A legnagyobb indukált feszültség értéke:
\(\displaystyle U_\text{max}=B\ell v_\text{max}=g\sqrt{mL}.\)
Megjegyzés. Nem tartozott a feladat kérdései közé, hogy megadjuk a rúd elmozdulásának, az indukálódó feszültségnek és az áramerősségnek időbeli változását. Ezt – elemi eszközökkel – úgy tehetjük meg, hogy felismerjük a feladatban szereplő folyamatok és a (kezdetben nyújtatlan) rugóra akasztott test harmonikus rezgőmozgása közötti hasonlóságot. Így beláthatjuk, hogy
\(\displaystyle x(t)=\frac{mgL}{B^2\ell^2} (1-\cos \omega t),\qquad v(t)= \frac{g\sqrt{mL}}{B \ell}\,\sin\omega t,\)
továbbá
\(\displaystyle U(t)= {g\sqrt{mL}} \,\sin\omega t \qquad \text{és} \qquad I(t)=\frac{mg}{B\ell}(1-\cos \omega t); \)
ahol \(\displaystyle \omega=\frac{B\ell}{\sqrt{mL}}\).
Statisztika:
8 dolgozat érkezett. 5 pontot kapott: Bokor Endre, Bonifert Balázs, Horváth 999 Anikó, Ludányi Levente, Nguyễn Đức Anh Quân, Tóth Ábel. 4 pontot kapott: Györgyfalvai Fanni. 1 pontot kapott: 1 versenyző.
A KöMaL 2019. decemberi fizika feladatai
