A P. 5464. feladat (2023. február)

P. 5464. Egy függőleges tengelyű, lefelé nyíló parabola \(\displaystyle F\) fókuszpontján keresztül különböző hajlásszögű lejtőket fektetünk. Mekkora a hajlásszöge annak a lejtőnek, amelyen az \(\displaystyle F\) pontból kezdősebesség nélkül induló, súrlódásmentesen lecsúszó pontszerű test a lehető legrövidebb idő alatt éri el a parabolát?

Faragó Andor (1877–1944) feladata nyomán\(\displaystyle ^*\)

*Faragó Andor indította újra 1925-ben az I. világháború miatt megszüntetett KöMaL-t, és annak 1938-ig szerkesztője, kiadója volt. Ő vezette be a kiemelkedő feladatmegoldók fényképeinek közlését.

(5 pont)

A beküldési határidő 2023. március 16-án LEJÁRT.

Megoldás. Legyen a parabola fókusztávolsága \(\displaystyle f\), és jelöljük a parabola \(\displaystyle P\) pontjának \(\displaystyle F\)-től mért távolságát \(\displaystyle s\)-sel. A parabola definíciója szerint a \(\displaystyle P\) pont az \(\displaystyle e\) vezéregyenestől is \(\displaystyle s\) távolságra van.

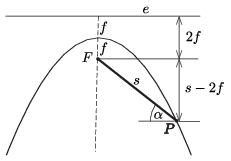
Az ábra szerint a \(\displaystyle P\) pontba érkező test lejtőjének hajlásszögére igaz, hogy

\(\displaystyle \sin\alpha=\dfrac{s-2f}{s}=1- 2\dfrac{f}{s},\)

és ennek megfelelően a test gyorsulása

\(\displaystyle a=g\sin\alpha=\left(1- 2\dfrac{f}{s}\right)g.\)

Ha a csúszás ideje \(\displaystyle t\), akkor az egyenletesen gyorsuló mozgás út-idő képlete szerint

\(\displaystyle t=\sqrt{\dfrac{2s}{a}},\)

vagyis

\(\displaystyle \dfrac{1}{t^2}=\dfrac{g}{2}\left(\dfrac{1}{s}-\dfrac{2f}{s^2}\right),\)

amit teljes négyzetté alakíthatunk:

\(\displaystyle \dfrac{1}{t^2}=\dfrac{g}{16\,f}-gf\left(\dfrac{1}{s}-\dfrac{1}{4f} \right)^2 \le \dfrac{g} {16\,f}=\dfrac{1}{t_\text{min}^2}.\)

Látszik, hogy a legrövidebb lecsúszási idő:

\(\displaystyle t_\text{min}=4\sqrt{\dfrac{f}{g}},\)

ami akkor valósul meg, amikor

\(\displaystyle s=4f, \qquad \sin\alpha=\dfrac{1}{2}, \qquad \alpha=30^\circ.\)

Statisztika:

41 dolgozat érkezett.
5 pontot kapott:	Beke Botond, Bencz Benedek, Bodré Zalán, Boér Panna Rita, Csilling Dániel, Csiszár András, Dercsényi Bence, Éger Viktória, Fajszi Karsa, Fehérvári Donát, Flóring Balázs, Fórizs Borbála, Halász Henrik, Hegedűs Máté Miklós, Kis Márton Tamás, Klement Tamás, Kovács Kristóf , Merics Vilmos, Molnár Kristóf, Molnár Zétény, Nagy 456 Imre, Nemeskéri Dániel, Papp Marcell Imre, Richlik Márton, Schmercz Blanka, Seprődi Barnabás Bendegúz, Szabó Márton, Szabó Zsombor, Tárnok Ede , Tóth Kolos Barnabás, Waldhauser Miklós.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	1 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2023. februári fizika feladatai