 |
A P. 5625. feladat (2025. február) |
P. 5625. Egy lovardában a lovas \(\displaystyle 20~\mathrm{m}\) sugarú körön állandó, \(\displaystyle 5~\mathrm{m}/\mathrm{s}\) nagyságú sebességgel jár körbe-körbe. A körben áll a lovászmester, a kör közepétől \(\displaystyle 10~\mathrm{m}\) távolságra. Mikor változik leglassabban, illetve leggyorsabban a lovas és a lovászmester közötti távolság? Mekkora sebességgel változik a közöttük lévő távolság ebben a két esetben?
Közli: Baranyai Klára, Veresegyház
(5 pont)
A beküldési határidő 2025. március 17-én LEJÁRT.
I. megoldás. Ha a lovas a legközelebb vagy a legtávolabb van a lovászmestertől, akkor éppen nem változik a közöttük lévő távolság. A kérdésre az a válasz, hogy akkor változik a leglassabban a lovas és a lovászmester közötti távolság, amikor a lovas éppen a legközelebbi ponton halad át, vagy éppen a legtávolabbi pont közelében mozog a 20 m sugarú pályáján. Ekkor a lovas és a lovászmester közötti távolság 10 m, illetve 30 m, a távolság állandósága miatt annak változási sebessége nulla.
Az ábrán kétféle nézőpontból láthatjuk a helyzetet. A bal oldali ábrán a talajhoz rögzített rendszerben a lovászmester (M) áll, a lovas (L) pedig 5 m/s kerületi sebességgel 20 m sugarú körpályán mozog. A jobb oldali ábrán lévő forgó rendszerben a lovas áll, és a lovászmester végez 10 m sugarú körön körmozgást ugyanazon középpont körül, 2,5 m/s nagyságú sebességgel, ellenkező körüljárás szerint.
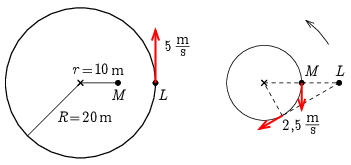
A jobb oldali ábráról leolvashatjuk, hogy akkor nő a leggyorsabban a lovas és a lovászmester közötti távolság, ha a lovászmester sebességének hatásvonalán helyezkedik el a lovas, ami éppen \(\displaystyle 60^\circ\)-os elfordulási szögnél következik be. Álló rendszerből ez ugyanakkora szögű, pozitív elfordulást jelent. Az ábráról leolvashatjuk azt is, hogy ebben a helyzetben a távolság növekedésének maximális üteme 2,5 m/s.
Ha a jobb oldali ábra félszabályos háromszögét tükrözzük az átfogóra, akkor azt a pontot kapjuk meg, ahol a leggyorsabban csökken a lovas és a lovászmester közötti távolság. A távolság csökkenési sebessége ilyenkor is 2,5 m/s.
II. megoldás Az előző megoldás jelöléseit kiegészítve legyen a lovas kerületi sebessége \(\displaystyle u\), a lovas \(\displaystyle L\) pozícióját a lovászmester \(\displaystyle M\) pozíciójával összekötő szakasz \(\displaystyle d\), a kör középpontja pedig \(\displaystyle O\)!
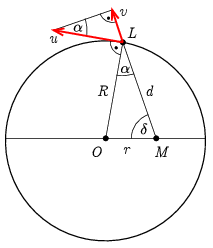
Nyilván akkor változik \(\displaystyle d\) a leggyorsabban, ha \(\displaystyle u\)-nak \(\displaystyle d\) irányára vett
\(\displaystyle v=u\sin{\alpha}\)
vetülete a legnagyobb. A merőleges szárú szögek egyenlősége miatt \(\displaystyle \alpha\) egyenlő az \(\displaystyle OLM\triangle\) \(\displaystyle L\)-nél lévő szögével. Ebben a háromszögben a szinusz-tétel szerint
\(\displaystyle \sin{\alpha}=\frac{r}{R}\sin{\delta},\)
ami akkor maximális, ha \(\displaystyle \sin{\delta}=1\), azaz \(\displaystyle \delta=\tfrac{\pi}{2}=90^\circ\). Ekkor \(\displaystyle \alpha=\tfrac{\pi}{6}=30^\circ\), ami a lovas \(\displaystyle \tfrac{\pi}{3}=60^\circ\)-os elfordulásakor következik be. Ilyenkor
\(\displaystyle v_\mathrm{max}=\frac{r}{R}u= 2{,}5\,\mathrm{\frac{m}{s}},\)
és \(\displaystyle d\) növekszik. Azt a pozíciót, amikor a \(\displaystyle d\) leggyorsabban csökken, a lovas megfelelő helyzetének az \(\displaystyle OM\) szakasz által kitűzött egyenesre való tükrözésével kapjuk meg.
III. megoldás. Jelöljük a lovas és a lovászmester közötti távolságot \(\displaystyle d\)-vel, a távolság változási sebességét \(\displaystyle v\)-vel, a sebességváltozás ütemét (vagyis \(\displaystyle d\) gyorsulását) \(\displaystyle a\)-val. Legyen a lovászmesterhez legközelebbi helyzethez képest a lovas (radiánokban mért) szögelfordulása \(\displaystyle \varphi\). Ha a távolságokat méter, az időt másodperc egységekben mérjük, akkor \(\displaystyle \varphi=t/4\).
A koszinusztétel alapján
| \(\displaystyle (1)\) | \(\displaystyle d^2=R^2+r^2-2Rr\cos(t/4)=500-400\,\cos(t/4),\) |
ennek az egyenletnek a deriválásából pedig
| \(\displaystyle (2)\) | \(\displaystyle 2vd=100\,\sin(t/4),\) |
vagyis
| \(\displaystyle (3)\) | \(\displaystyle v=\frac{50\,\sin(t/4)}{\sqrt{500-400\,\cos(t/4)}}.\) |
A lovas és a lovászmester közötti távolság akkor változik a leglassabban, amikor a változás pillanatnyi sebessége nulla. (3) szerint ez \(\displaystyle t=0\) és \(\displaystyle t=4\pi\) időpontokban, vagyis a \(\displaystyle \varphi=0\), valamint \(\displaystyle \varphi=\pi\) (és azoktól \(\displaystyle 2\pi\) egész számú többszörösével eltérő) szögeknél következik be, ekkor kerül a lovas a legközelebb, illetve legtávolabb a lovászmestertől.
A távolság változási sebességének abszolút értéke akkor a legnagyobb, amikor \(\displaystyle v\) maximális, illetve minimális értékű. Mindkét esetben \(\displaystyle v(t)\) változási sebessége (idő szerinti deriváltja), vagyis az \(\displaystyle a\) gyorsulás nulla.
(2) ismételt deriválásával,
\(\displaystyle 2ad+2v^2=25\,\cos(t/4),\)
ahonnan (3), valamint \(\displaystyle a=0\) felhasználásával kapjuk:
\(\displaystyle 2\frac{50^2\,\sin^2(t/4)}{500-400\, \cos(t/4)}=25\,\cos(t/4).\)
Ebből következik:
| \(\displaystyle (4)\) | \(\displaystyle 2\cfrac{\sin^2(t/4)}{5-4\cos(t/4)}=\cos(t/4).\) |
Bevezetve a \(\displaystyle \xi=\cos(t/4)\) jelölést (4) másodfokú egyenletté alakul:
\(\displaystyle \xi^2-\frac{5}{2}\xi+1=0.\)
Ennek \(\displaystyle \vert\xi\vert\le1\) megoldása:
\(\displaystyle \xi=\frac{1}{2},\qquad \varphi=\frac{t}{4}=\pm\frac{\pi}{3}.\)
Mindkét esetben (3) szerint \(\displaystyle \vert v\vert=2{,}5\,\mathrm{m/s}\). Ekkora sebességgel növekszik a \(\displaystyle d\) távolság akkor, amikor a lovas a teljes kör 1/6-át tette meg, a körpálya 5/6 részénél pedig ekkora sebességgel csökken a lovas és a lovászmester közötti távolság.
Statisztika:
30 dolgozat érkezett. 5 pontot kapott: Bálint Áron, Beke Márton Csaba, Bencze Mátyás, Elekes Panni, Erdélyi Dominik, Erős Fanni, Gyenes Károly, Kis Boglárka 08, Kovács Tamás, Magyar Zsófia, Molnár Lili, Simon János Dániel, Tóth Hanga Katalin, Vincze Anna. 4 pontot kapott: Bélteki Teó, Magyar Levente Árpád, Sütő Áron. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2025. februári fizika feladatai

