 |
A P. 5631. feladat (2025. február) |
P. 5631. Közismert, hogy egy egyenletesen töltött, vékony, nagyon hosszú, egyenes száltól \(\displaystyle R\) távolságra mekkora az elektromos térerősség. Hasonlítsuk össze ezt a térerősséget egy \(\displaystyle R\) sugarú félkör középpontjában létrejövő térerősséggel, feltételezve, hogy a félkört egy ugyanolyan tulajdonságú, ugyanolyan vonalmenti töltéssűrűségű szálból készítettük!
Amerikai feladat nyomán
(5 pont)
A beküldési határidő 2025. március 17-én LEJÁRT.
I. megoldás. Legyen a szál vonalmenti töltéssűrűsége (egységnyi hosszúságú darabjának töltése) \(\displaystyle \lambda\). A nagyon hosszú, egyenes száltól \(\displaystyle R\) távolságban az elektromos térerősség nagysága
| \(\displaystyle (1)\) | \(\displaystyle E_1=\frac{1}{2\pi\varepsilon_0}\,\frac{\lambda}{R},\) |
amit a \(\displaystyle k=1/(4\pi\varepsilon_0)\) Coulomb-állandóval kifejezve így is felírhatunk:
| \(\displaystyle (1')\) | \(\displaystyle E_1=2k\frac{\lambda}{R}.\) |
Megjegyzés. A fenti képlet helyességét pl. a Gauss-féle fluxustörvényből is megkaphatjuk. A szál \(\displaystyle \ell\) hosszúságú darabjának töltése \(\displaystyle Q=\lambda\ell\). Ha a szálat koaxiálisan körülvesszük egy \(\displaystyle R\) sugarú hengerrel, annak palástjára vonatkoztatott elektromos fluxus \(\displaystyle \Psi=2R\pi\ell E_1.\) A fluxustörvény szerint \(\displaystyle \Psi=\tfrac{1}{\varepsilon_0}Q\), ezekből pedig (1) már következik.
Tekintsük most az \(\displaystyle R\) sugarú, félkör alakú szál esetét. A félkör \(\displaystyle O\) középpontjában az elektromos térerősség iránya a félkör szimmetriatengelye, nagysága pedig legyen \(\displaystyle E_2\). Ha a félkör középpontjába egy \(\displaystyle q\) nagyságú ponttöltést helyezünk, arra \(\displaystyle qE_2\) nagyságú erő hat. Ugyanekkora nagyságú, de ellentétes irányú erőt fejt ki a ponttöltés az egyenletesen töltött szálra.
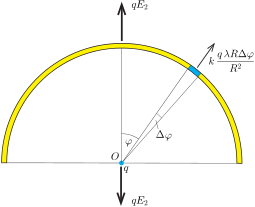
1. ábra
A félkör alakú szálnak egy kicsiny, \(\displaystyle O\)-ból nézve \(\displaystyle \Delta\varphi\) szög alatt látszó darabkájának töltése \(\displaystyle \lambda R\Delta\varphi,\) erre tehát a \(\displaystyle q\) töltés
\(\displaystyle \Delta F=k\frac{q\,\lambda R\Delta\varphi}{R^2}\)
nagyságú, sugár irányban ,,kifelé'' mutató erőt fejt ki. Ezen erőnek a szimmetriatengely irányú komponense \(\displaystyle \Delta F \cos\varphi\), ahonnan az egyes darabkák járulékainak összegzésével kapjuk, hogy
\(\displaystyle qE_2=\sum k\frac{q\,\lambda R\Delta\varphi}{R^2}\,\cos\varphi.\)
Innen – a felosztás finomításával integrálásra áttérve – adódik a keresett eredmény:
\(\displaystyle E_2=k\frac{\lambda}{R}\int\limits_{-\pi/2}^{\pi/2}\cos\varphi\,\mathrm{d}\varphi.\)
Az integrál számértéke 2, így (1')-vel összevetve megállapíthatjuk, hogy \(\displaystyle E_2=E_1\), vagyis a kétféle elrendezés térerőssége a vizsgált pontban ugyanakkora.
Megjegyzés. A félkörre ható eredő erő nagyságát integrálszámítás nélkül is meghatározhatjuk. Megállapíthatjuk, hogy a félkör alakú szálra hosszegységenként \(\displaystyle p=kq\lambda/R^2\) nagyságú, a száldarabka érintőjére merőleges irányú erő hat. (\(\displaystyle p\) a folyadékok nyomásához hasonló, ,,vonalmenti nyomásként'' értelmezhető mennyiség.) Egészítsük ki a félkör-szálat egy a végpontjai között elhelyezkedő, \(\displaystyle 2R\) hosszúságú egyenes darabbal, aminek ugyanakkora a töltéssűrűsége, mint a félköré. Ha erre az egyenes szálra is \(\displaystyle p\) ,,nyomást'', tehát \(\displaystyle 2Rp\) nagyságú erőt fejtünk ki, akkor a zárt hurokra ható eredő erő nullává válik. (Analóg helyzet: egy zárt tartályra a benne lévő gáz nyomása nem fejt ki eredő erőt.) Ennek megfelelően a félkörre ható \(\displaystyle qE_2\) elektromos erő is \(\displaystyle 2Rp=2kq\lambda/R\) nagyságú, azaz \(\displaystyle E_2=E_1\) teljesül.
II. megoldás. A két töltött szál \(\displaystyle O\) pontbeli elektromos térerősségét anélkül is össze tudjuk hasonlítani, hogy bármelyik térerősség nagyságát kiszámítanánk. Megmutatjuk, hogy a két szál egymásnak megfeleltethető kicsiny darabkáinak térerőssége ugyanolyan irányú és ugyanolyan nagyságú vektor, emiatt ezeknek a vektoroknak az összege, vagyis az eredő elektromos térerősség a kétféle alakú szálra ugyanakkora.
Tekintsük a félkörív és az egyenes szál azon kicsiny darabkáit, amelyek az \(\displaystyle O\) pontból nézve ugyanolyan irányban és ugyanakkora szög alatt látszanak.
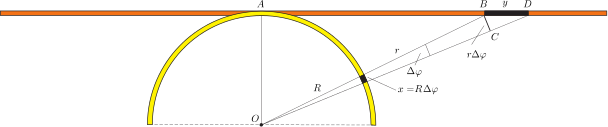
2. ábra
A 2. ábra jelöléseit követve megállapíthatjuk, hogy a körív alakú szál kicsiny \(\displaystyle x=R\Delta\varphi\) hosszúságú ívén \(\displaystyle Q_1=\lambda x\) töltés, az egyenes szál \(\displaystyle y\) hosszúságú részén pedig \(\displaystyle Q_2=\lambda y\) töltés található. Ezek a töltések az \(\displaystyle O\) pontban
\(\displaystyle E_1=k\lambda\frac{x}{R^2},\qquad\textrm{illetve}\qquad E_2=k\lambda\frac{y}{r^2}\)
nagyságú elektromos térerősséget hoznak létre. Ez a két térerősség azonban egyforma nagy, hiszen az \(\displaystyle OAB\triangle\) és a \(\displaystyle BCD\triangle\) hasonlósága miatt
\(\displaystyle \frac{r}{R}=\frac{y}{r\Delta\varphi}=\frac{yR}{xr},\qquad\textrm{tehát}\qquad\frac{y}{r^2}=\frac{x}{R^2}.\)
A fenti megfontolások során kihasználtuk, hogy \(\displaystyle x\ll R\) és \(\displaystyle y\ll r\), vagyis a szálak kis darabkáinak látószöge nagyon kicsi, emiatt a kicsiny körívek hossza és a megfelelő húrok hossza egyenlőnek vehető.
Statisztika:
22 dolgozat érkezett. 5 pontot kapott: Beke Márton Csaba, Bélteki Teó, Erdélyi Dominik, Gyenes Károly, Kiss 131 Adorján Timon, Klement Tamás, Simon János Dániel, Szécsi Bence, Tóth Hanga Katalin, Ujpál Bálint, Zólomy Csanád Zsolt. 4 pontot kapott: Hornok Máté, Kovács Tamás, Papp Emese Petra, Ujvári Sarolta. 3 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző.
A KöMaL 2025. februári fizika feladatai
