A P. 5632. feladat (2025. február)

P. 5632. Egy nagy méretű fémlemez egyik oldalán egy \(\displaystyle Q\) és egy \(\displaystyle -Q\) töltésű, pontszerűnek tekinthető golyócska van, egymástól \(\displaystyle d\), a lemeztől \(\displaystyle d/2\) távolságra. Mekkora munkával tudjuk a töltéseket

a) a lemez síkjával párhuzamosan mozgatva egymástól nagyon messzire eltávolítani,

b) a lemezre merőlegesen mozgatva a lemeztől nagyon messzire (azonos távolságra) elmozdítani,

c) a lemeztől és egymástól is nagyon messzire vinni?

Közli: Cserti József, Budapest

(5 pont)

A beküldési határidő 2025. március 17-én LEJÁRT.

Megoldás. Egy nagy méretű fémlemez egyik oldalán lévő kicsiny töltés megosztást hoz létre a fémlemezben, és a kialakuló elektromos mező olyan lesz, mintha a kis töltés helyének a lemezre vett tükörkép-pontjában egy vele azonos nagyságú, de ellentétes töltésű másik test, az úgynevezett tükörtöltés helyezkedne el. Ez az elektromos mező a fémlemeznek csak az egyik (a valódi töltéssel megegyező) oldalán alakul ki, a másik oldalon a térerősség mindenhol nulla.

Két kicsiny töltött test és a nagy méretű fémlemez elektromos terét a két töltés és a nekik megfelelő két tükörtöltés együttese határozza meg (lásd az ábrát).

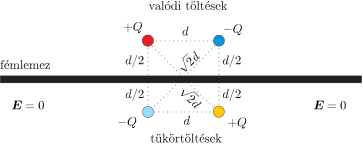
Egy ilyen elrendezés elektrosztatikus (kölcsönhatási) energiáját a páronkénti Coulomb-energiák összege adja meg, de mivel elektromos mező a fémlemeznek csak az egyik oldalán alakul ki, az összenergia csak a fele annak, amekkora 4 valódi töltés esetében lenne. Esetünkben a kezdeti elrendezés energiája

\(\displaystyle {\cal E}_0=\frac{1}{2}\cdot kQ^2\left(-\frac{1}{d}-\frac{1}{d}-\frac{1}{d}-\frac{1}{d}+\frac{1}{\sqrt{2}d}+ \frac{1}{\sqrt{2}d}\right)=\frac{kQ^2}{d}\left(\frac{1}{\sqrt{2}}-2\right).\)

Hasonló módon számíthatjuk ki a különböző módon eltávolított töltések elektrosztatikus energiáját is:

\(\displaystyle {\cal E}_a={\cal E}_b=-\frac{kQ^2}{d}\qquad\textrm{és}\qquad{\cal E}_c=0.\)

(Az egymástól ,,nagyon messzire'' kerülő töltések kölcsönhatási energiája – jó közelítéssel – nullának tekinthető.)

A töltések megadott módon történő elmozdítása során végzett munka az elektrosztatikus energia megváltozásával (növekedésével) egyenlő.

\(\displaystyle W_a={\cal E}_a-{\cal E}_0=\frac{kQ^2}{d}\left(1-\frac{1}{\sqrt{2}}\right),\)

\(\displaystyle W_b={\cal E}_b-{\cal E}_0=\frac{kQ^2}{d}\left(1-\frac{1}{\sqrt{2}}\right),\)

\(\displaystyle W_c={\cal E}_c-{\cal E}_0=\frac{kQ^2}{d}\left(2-\frac{1}{\sqrt{2}}\right).\)

Statisztika:

6 dolgozat érkezett.
4 pontot kapott:	Kovács Tamás, Simon János Dániel, Ujpál Bálint, Vértesi Janka.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.

A KöMaL 2025. februári fizika feladatai