A P. 5638. feladat (2025. március)

P. 5638. Egy magában álló semleges fémgömb középpontjától $\displaystyle d$ távolságra, kívül lévő $\displaystyle Q$ pontszerű töltést $\displaystyle 2d$ távolságra távolítjuk. Mennyit változik a fémgömb potenciálja eközben?

Közli: Simon Péter, Pécs

(5 pont)

A beküldési határidő 2025. április 15-én LEJÁRT.

I. megoldás. Egy fémgömb közelébe helyezett ponttöltés megosztást hoz létre a fémgömbön. A töltések úgy mozdulnak el a fém felületén, hogy a gömb ekvipotenciálissá váljon. A kialakuló elektromos mező a gömbön kívül olyan, mintha a gömb belsejében megfelelő helyen megfelelő nagyságú ,,tükörtöltés'' helyezkedne el, és a fém nem is lenne ott. (Ez a gömbi tükörtöltés módszere, amelyről részletesen olvashatunk pl. a KöMaL 2022. évi decemberi számában megjelent P. 5453. feladat megoldásánál.)

Ha egy $\displaystyle R$ sugarú fémgömb középpontjától $\displaystyle d$ távolságra egy pontszerű $\displaystyle Q$ töltés található, akkor a fémfelület akkor válik nulla potenciálúvá, ha a gömb középpontjától $\displaystyle x=R^2/d$ távolságban egy $\displaystyle q=-\frac{R}{d}Q$ nagyságú tükörtöltést helyezünk el. Ha a fémgömb nem földelt, de az össztöltése nulla, akkor a gömbhéj potenciálja nem lesz nulla, de a felülete továbbra is ekvipotenciális marad. Ezt az erőteret a külső $\displaystyle Q$ töltés, a gömbön belüli $\displaystyle q$ töltés, valamint a gömb középpontjába helyezett $\displaystyle -q=\frac{R}{d}Q$ töltés tudja létrehozni. A fémgömb potenciálja ilyenkor

$\displaystyle \Phi(d)=-\frac{1}{4\pi\varepsilon_0}\frac{q}{R}=\frac{1}{4\pi\varepsilon_0}\frac{Q}{d}$

lesz. (A potenciált a ,,végtelen'' távoli pontokban választottuk nullának.)

Ha a $\displaystyle Q$ töltést $\displaystyle 2d$ távolra visszük, a fémgömb potenciálja

$\displaystyle \Phi(2d)=\frac{1}{4\pi\varepsilon_0}\frac{Q}{2d}$

lesz. A potenciál megváltozása

$\displaystyle \Delta\Phi=\Phi(2d)-\Phi(d)=-\frac{1}{4\pi\varepsilon_0}\frac{Q}{2d}.$

Ha $\displaystyle Q>0,$ akkor $\displaystyle \Delta\Phi<0,$ vagyis a fémgömb elektromos potenciálja lecsökken.

II. megoldás. A feladatot a gömbi tükörtöltés módszerének ismerete nélkül is meg lehet oldani. Tekintsük a fémgömb és a pontszerű töltés rendszerének az ábrán látható 4-féle állapotát:

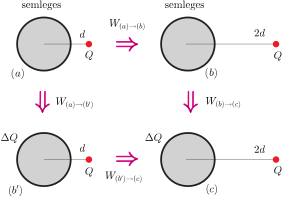
(a) Kezdetben a fémgömb semleges, és a $\displaystyle Q$ töltés a gömb középpontjától $\displaystyle d$ távolságra van.

(b) A fémgömb semleges, de a ponttöltést a gömb középpontjától $\displaystyle 2d$ távolságra található.

(b') A ponttöltés $\displaystyle d$ távolságra van a gömb középpontjától, de a fémgömb nem semleges, hanem kicsiny, $\displaystyle \Delta Q\ll Q$ töltéssel rendelkezik.

(c) A ponttöltés $\displaystyle 2d$ távolságra van a $\displaystyle \Delta Q$ töltésű gömb középpontjától.

Számítsuk ki, hogy mekkora munkavégzéssel tudjuk a rendszert az (a) állapotból egyszer (b)-n, másodszor pedig (b')-n keresztül a (c) állapotba vinni.

A $\displaystyle Q$ töltés a semleges fémgömbön elektromos megosztást hoz létre, amelynek elektromos mezője valamilyen (helyről helyre változó) erőt fejt ki a ponttöltésre. A $\displaystyle Q$ töltést valamekkora

$\displaystyle W_{(a)\rightarrow(b)}=W_0$

munkát végezve juttathatjuk el $\displaystyle d$-től $\displaystyle 2d$ távolságig. (Ennek a munkának a nagyságát ki lehet számítani, de erre – szerencsére – nem lesz szükségünk.)

Ha a (b) állapotban a fémgömb potenciálja $\displaystyle \Phi(2d)$, akkor nagyon (,,végtelen'') messziről kicsiny $\displaystyle \Delta Q$ töltést

$\displaystyle W_{(b)\rightarrow(c)}=\Delta Q\cdot\Phi(2d)$

munkával tudunk a fémgömbre juttatni. (Ez a potenciál definíciójából következik.)

Járjuk most végig a másik ,,útvonalat''. A fémgömbre

$\displaystyle W_{(a)\rightarrow(b')}=\Delta Q\cdot\Phi(d)$

munkával tudunk $\displaystyle \Delta Q$ töltést eljuttatni, ahol $\displaystyle \Phi(d)$ a fémgömb potenciálja a $\displaystyle Q$ töltés közelebbi helyzetében.

Végül számítsuk ki, hogy mekkora munkával tudjuk a kicsiny töltéssel rendelkező gömbtől a $\displaystyle Q$ töltést $\displaystyle d$-től $\displaystyle 2d$-ig eltávolítani. Az elektromos erőtér ebben az esetben a megosztásból származó térerősségek és a $\displaystyle \Delta Q$ töltés elektromos terének szuperpozíciója. Az előbbi erőtérben végzett munka a korábban szereplő $\displaystyle W_0$-lal egyezik meg. A $\displaystyle \Delta Q$ töltés által létrehozott elektromos mező – a gömbön kívül – egy pontszerű töltés Coulomb-terével egyezik meg, ennek ellenében végzett munka tehát a Coulomb-energia megváltozásával egyenlő. Így

$\displaystyle W_{(b')\rightarrow(c)}=W_0+\frac{Q\cdot\Delta Q}{4\pi\varepsilon_0}\left(\frac{1}{2d}-\frac{1}{d}\right).$

A végzett munka az elektromos mező energiájának megváltozásával egyenlő, emiatt független attól, hogy milyen közbenső állapoton keresztül jutottunk el (a)-ból (c)-be:

$\displaystyle W_{(a)\rightarrow(b)}+W_{(b)\rightarrow(c)}=W_{(a)\rightarrow(b')}+W_{(b')\rightarrow(c)},$

azaz

$\displaystyle W_0+\Delta Q\cdot\Phi(2d)=\Delta Q\cdot\Phi(d)+\left(W_0-\frac{Q\cdot\Delta Q}{4\pi\varepsilon_0}\frac{1}{2d}\right).$

Innen kapjuk, hogy a fémgömb potenciáljának megváltozása

$\displaystyle \Phi(2d)-\Phi(d)=-\frac{1}{4\pi\varepsilon_0}\frac{Q}{2d}.$

III. megoldás. A $\displaystyle \Phi(d)$ potenciált egy egyszerű meggondolással is megkaphatjuk. A fémgömb felületén a $\displaystyle Q$ töltés okozta elektromos megosztás miatt valamilyen $\displaystyle \varrho(\vec{R})$ töltéssűrűség alakul ki, és a tér bármely pontjában a potenciál ezen töltéseloszlás és a különálló $\displaystyle Q$ töltés potenciáljának összegeként adható meg. Mivel a fémgömb minden pontja azonos potenciálon van, ennek meghatározásához kézenfekvő, hogy a legegyszerűbb leírást kínáló pontot, a gömb középpontját válasszuk. A gömbfelület $\displaystyle \vec{R}$-rel jellemezhető pontja körüli kis $\displaystyle \Delta A$ felület töltése $\displaystyle \Delta q=\varrho(\vec{R})\Delta A$, így

$\displaystyle \Phi(d)=\frac{1}{4\pi\varepsilon_0}\sum\frac{\Delta q}{R}+\frac{1}{4\pi\varepsilon_0}\frac{Q}{d}.$

Mivel a gömb semleges, $\displaystyle \sum\Delta q=0$, tehát

$\displaystyle \Phi(d)=\frac{1}{4\pi\varepsilon_0}\frac{Q}{d}.$

Statisztika:

19 dolgozat érkezett.
5 pontot kapott:	Beke Márton Csaba, Erdélyi Dominik, Klement Tamás, Pituk Péter, Poló Zsófia , Simon János Dániel, Tóth Bertalan, Varga Zétény.
4 pontot kapott:	Balázs Barnabás, Bor Noémi, Kávai Ádám, Konkoly Zoltán, Ujvári Sarolta.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	2 versenyző.

A KöMaL 2025. márciusi fizika feladatai