A P. 5640. feladat (2025. március)

P. 5640. A Kanári-szigetek legnagyobb városában, Las Palmasban található egy Európában egyedülálló kiállítás, amely a Föld vizeinek élővilágát mutatja be. A kiállítás egyik attrakciója egy $\displaystyle 400$ köbméteres, függőleges, henger alakú tengeri akvárium, melynek karbantartását búvárok végzik. Vízszintesen körbenézve az akvárium falának hányad részén lát ki az a búvár, aki az $\displaystyle R$ sugarú henger szimmetriatengelyétől $\displaystyle d$ távolságra van? A tengervíz törésmutatója $\displaystyle n$.

Közli: Vigh Máté, Herceghalom

(5 pont)

A beküldési határidő 2025. április 15-én LEJÁRT.

Megoldás. Az alábbi felülnézeti ábrán az akváriumot az $\displaystyle O_1$ középpontú $\displaystyle k_1$ kör szemlélteti, a búvár helyzetét pedig a $\displaystyle B$ pont. Mivel a fény útja megfordítható, a kérdést feltehetjük így is: a $\displaystyle B$ pontból vízszintesen kiinduló fénysugarak a $\displaystyle k_1$ kör mely részén tudnak kilépni az akváriumból?

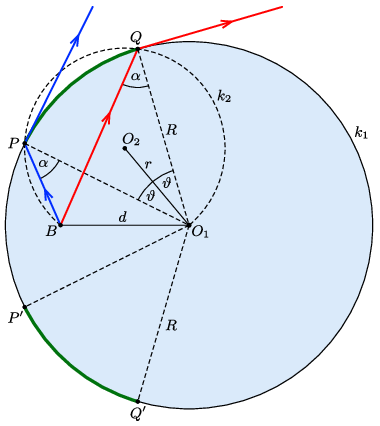
Egy fénysugár kilépésének feltétele, hogy a beesési szög kisebb legyen a teljes visszaverődés $\displaystyle \alpha=\arcsin(1/n)$ határszögénél. (Könnyen belátható, hogy ez akkor is igaz marad, ha az akvárium falának fénytörését is figyelembe vesszük, feltéve, hogy a falvastagság sokkal kisebb az $\displaystyle R$ sugár értékénél.) Tekintsünk egy olyan fénysugarat, amely éppen a kritikus $\displaystyle \alpha$ beesési szögben, valamely $\displaystyle P$ pontban érkezik az akvárium falához (lásd a kék töröttvonalat az ábrán). A $\displaystyle P$ pont tehát rajta van a $\displaystyle BO_1$ szakaszhoz tartozó, $\displaystyle \alpha$ szögű $\displaystyle k_2$ látószögköríven; jelöljük ennek középpontját $\displaystyle O_2$-vel! A $\displaystyle k_2$ körív az eredeti $\displaystyle k_1$ kört nem csak a $\displaystyle P$ pontban, hanem egy másik $\displaystyle Q$ pontban is metszi, azaz létezik egy másik fénysugár is (az ábrán a piros töröttvonal), amely a teljes visszaverődés határhelyzetében halad. A $\displaystyle k_1$ kör (rövidebb) $\displaystyle PQ$ íve mentén az akvárium falát elérő fénysugarak mind teljes visszaverődést szenvednek, mert ezekből a pontokból nézve a $\displaystyle BO_1$ szakasz $\displaystyle \alpha$-nál nagyobb szögek alatt látszik. Ugyancsak nem jut ki fény a $\displaystyle PQ$ körív $\displaystyle BO_1$ tengelyre való tükrözésével kapott $\displaystyle P'Q'$ köríven sem. Ha a $\displaystyle k_1$ kör $\displaystyle PQ$ ívéhez tartozó középponti szöget $\displaystyle 2\vartheta$ módon jelöljük, akkor a $\displaystyle k_1$ kör kerületének

$\displaystyle \eta=\frac{2\pi-4\vartheta}{2\pi}=1-\frac{2\vartheta}{\pi}$

hányadát tudja fény elhagyni.

Hátra van még a $\displaystyle \vartheta$ szög meghatározása. Ehhez először is vegyük észre, hogy az $\displaystyle O_1O_2B$ háromszög egyenlőszárú, valamint a kerületi és középponti szögek tétele miatt $\displaystyle O_1O_2B\angle=2\alpha$. Ennek segítségével a $\displaystyle k_2$ körív sugara kiszámítható:

$\displaystyle r=\frac{d}{2\sin\alpha}=\frac{nd}{2}.$

Most tekintsük a szintén egyenlőszárú $\displaystyle O_1O_2P$ háromszöget, melyben a $\displaystyle \vartheta$ szög koszinusza így írható:

$\displaystyle \cos\vartheta=\frac{R}{2r}=\frac{R}{nd}.$

Mindezek felhasználásával a feladat kérdésére a válasz megadható:

$\displaystyle \eta=1-\frac{2}{\pi}\arccos\frac{R}{nd}.$

Ennek az eredménynek csak $\displaystyle R/(nd)\leq 1$ esetén van értelme. Ha a búvár $\displaystyle d\leq R/n$ távolságra van az akvárium szimmetriatengelyétől, akkor víszintesen körbenézve minden irányban kilát a tartályból, azaz $\displaystyle \eta=1$.

Statisztika:

A P. 5640. feladat értékelése még nem fejeződött be.

A KöMaL 2025. márciusi fizika feladatai