 |
A P. 5644. feladat (2025. április) |
P. 5644. Milyen egyetlen, \(\displaystyle m\) tömeggel kellene helyettesíteni az ábrán szereplő jobb oldali csigát és a rajta lévő tömegeket, hogy az \(\displaystyle m_{1}\) tömegű test ugyanúgy mozogjon, mint az eredeti elrendezésben? Hanyagoljuk el a csigák tömegét és a súrlódást.
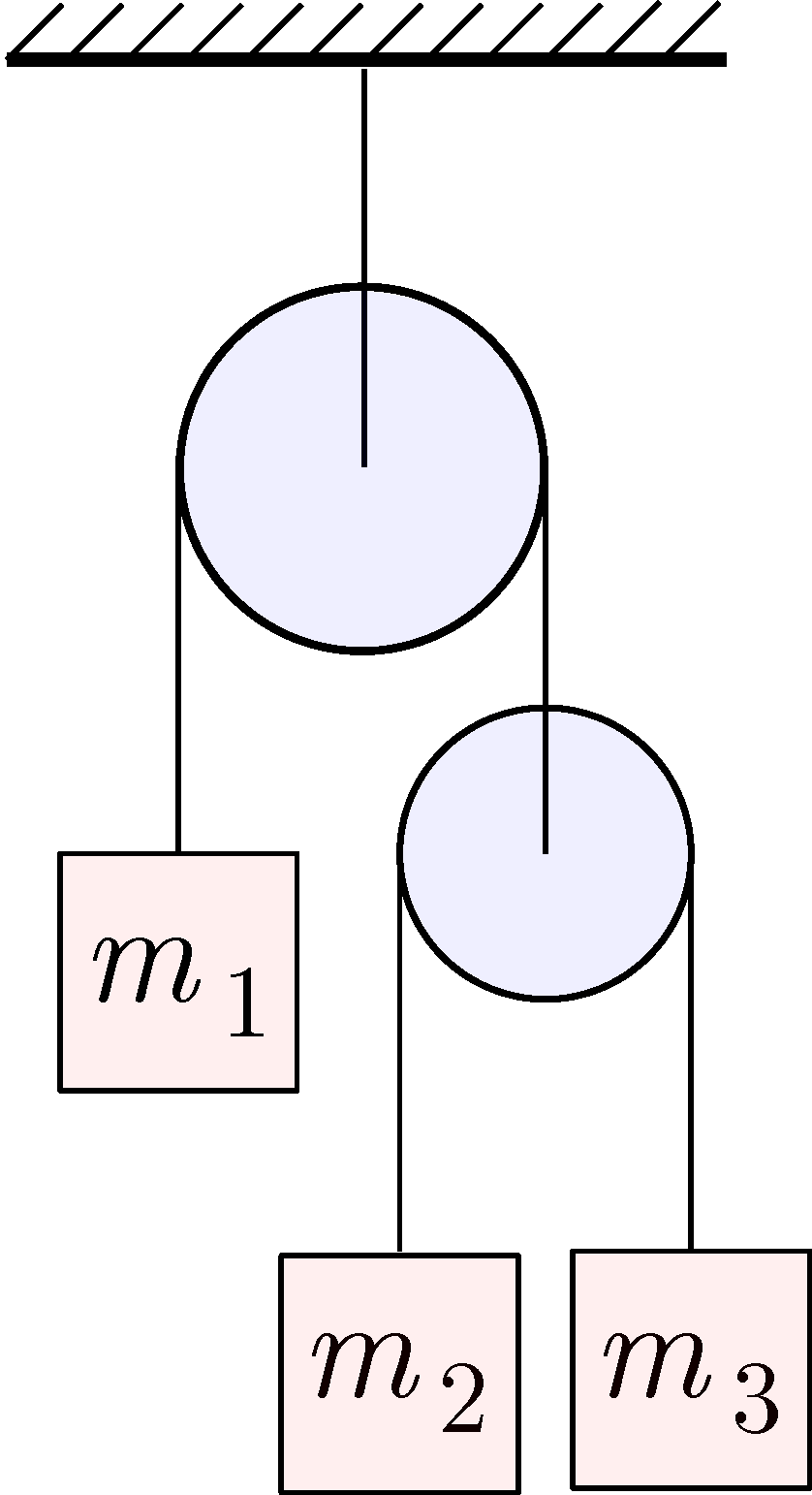
Közli: Siposs András, Budapest
(4 pont)
A beküldési határidő 2025. május 15-én LEJÁRT.
I. megoldás. Vizsgáljuk a mozgást a jobb oldali csigával együtt mozgó vonatkoztatási rendszerben. A csiga gyorsulása legyen \(\displaystyle a^\star\), és vegyük felfelé pozitívnak (értéke az adatoktól függően pozitív, negatív vagy zérus is lehet). Ebben a rendszerben vizsgálva a mozgást az \(\displaystyle m_i\) tömegű testre az \(\displaystyle m_ig\) nehézségi erőn kívül egy \(\displaystyle m_ia^\star\) nagyságú, lefelé mutató tehetetlenségi erő hatását is figyelembe kell vennünk, tehát olyan, mintha a nehézségi gyorsulás értéke \(\displaystyle g^\star=g+a^\star\) lenne.

1. ábra
Az 1. ábra alapján a mozgásegyenletek (\(\displaystyle m_2\geq m_3\) feltételezéssel, de ennek az indexek felcserélhetősége miatt nincs jelentősége):
$$\begin{gather*} m_2a=m_2g^\star-K,\\ m_3a=K-m_3g^\star. \end{gather*}$$Ebből
\(\displaystyle a=\frac{m_2-m_3}{m_2+m_3}g^\star\qquad\textrm{és}\qquad K=\frac{2m_2m_3}{m_2+m_3}g^\star.\)
A csigát tartó kötélre (a csiga elhanyagolható tömege miatt) \(\displaystyle 2K\) erő hat. Ha a csigát és a két rajta lógó testet egyetlen \(\displaystyle m\) tömeggel helyettesítenénk, akkor arra – mivel ebben a rendszerben nyugalomban van – \(\displaystyle mg^\star\) erő hatna. Tehát a keresett tömeg:
\(\displaystyle m=\frac{2K}{g^\star}=\frac{4m_2m_3}{m_2+m_3}.\)
II. megoldás.
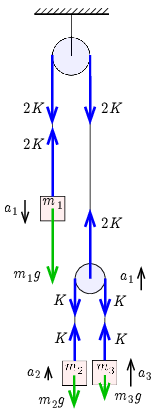
2. ábra
Inerciarendszerben az egész rendszert vizsgáljuk. A 2. ábra alapján a mozgásegyenletek és a kényszerfeltétel:
$$\begin{gather*} m_1a_1=m_1g-2K,\\ m_2a_2=K-m_2g,\\ m_3a_3=K-m_3g,\\ a_3-a_1=a_1-a_2. \end{gather*}$$A lineáris egyenletrendszer megoldása (\(\displaystyle a_2\) és \(\displaystyle a_3\) kifejezésére nem lesz szükségünk, azt csak a teljesség kedvéért írjuk fel):
$$\begin{gather*} a_1=\frac{m_1(m_2+m_3)-4m_2m_3}{m_1(m_2+m_3)+4m_2m_3}g,\\ a_2=\frac{4m_3(m_1-m_2)-m_1(m_2+m_3)}{m_1(m_2+m_3)+4m_2m_3}g,\\ a_3=\frac{4m_2(m_1-m_3)-m_1(m_2+m_3)}{m_1(m_2+m_3)+4m_2m_3}g,\\ K=\frac{4m_1m_2m_3g}{m_1(m_2+m_3)+4m_2m_3}. \end{gather*}$$Ha a jobb oldali csiga és a rajta lógó tömegek helyett egyetlen tömeg lenne, akkor annak a mozgásegyenlete így nézne ki:
\(\displaystyle ma_1=2K-mg.\)
Ebből a keresett tömeg \(\displaystyle K\) és \(\displaystyle a_1\) behelyettesítésével:
\(\displaystyle m=\frac{2K}{a_1+g}=\frac{\frac{8m_1m_2m_3g}{m_1(m_2+m_3)+4m_2m_3}}{\left(\frac{m_1(m_2+m_3)-4m_2m_3}{m_1(m_2+m_3)+4m_2m_3}+1\right)g}=\frac{\frac{8m_1m_2m_3g}{m_1(m_2+m_3)+4m_2m_3}}{\frac{2m_1(m_2+m_3)g}{m_1(m_2+m_3)+4m_2m_3}}=\frac{4m_2m_3}{m_2+m_3},\)
az első megoldással megegyezően.
Megjegyzés. Észrevehetjük, hogy a végeredmény nem függ \(\displaystyle m_1\)-től. Így inerciarendszerben is megoldhatjuk a feladatot az I. megoldáshoz hasonlóan: \(\displaystyle a_1\) értékét ne akarjuk meghatározni (,,bízva'' abban, hogy úgyis kiesik a végeredményből), hanem vegyük fel paraméternek. Ekkor a két jobb oldali test mozgásegyenlete és a kényszerfeltétel a 2. ábra alapján:
$$\begin{gather*} m_2a_2=K-m_2g,\\ m_3a_3=K-m_3g,\\ a_3-a_1=a_1-a_2. \end{gather*}$$Ebből
\(\displaystyle K=\frac{2m_2m_3(a_1+g)}{m_2+m_3},\)
és
\(\displaystyle m=\frac{2K}{a_1+g}=\frac{4m_2m_3}{m_2+m_3}\)
azonnal adódik.
Persze ez ,,bújtatva'' az I. megoldás, hiszen \(\displaystyle a_1\) éppen \(\displaystyle a^\star\)-gal, és így \(\displaystyle a_1+g\) pedig \(\displaystyle g^\star\)-gal egyezik meg.
Statisztika:
24 dolgozat érkezett. 4 pontot kapott: Bencze Mátyás, Csipkó Hanga Zoé , Csiszár András, Molnár Lili, Papp Emese Petra, Szécsi Bence, Vértesi Janka, Zádori Gellért. 3 pontot kapott: Bélteki Teó, Fekete Lúcia, Konkoly Zoltán. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2025. áprilisi fizika feladatai
