 |
A P. 5646. feladat (2025. április) |
P. 5646. Űrutazást terveznek a Marsra. Az űrhajó a Földet elhagyva olyan ellipszis pályára áll, amely érinti a két bolygópályát, perihéliumába esik a felszállás, aphéliumába pedig a megérkezés. A visszaút hasonló ellipszispályán történik. Az induláshoz mindkét esetben ki kell várni, amíg a két bolygó megfelelő helyzetbe kerül. Mennyi ideig tart az oda-, illetve visszaút, és legalább mennyi időt fognak a Marson tölteni? A bolygópályákat tekintsük azonos síkban fekvő köröknek, a Mars keringési ideje \(\displaystyle 687{,}0\) földi nap.
Közli: Vladár Károly, Kiskunhalas
(5 pont)
A beküldési határidő 2025. május 15-én LEJÁRT.
Megoldás.
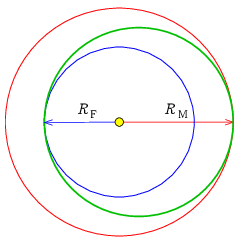
Az oda és a visszautazás időtartama egyaránt az űrhajó ellipszispályájához tartozó keringési idő fele. Az ellipszis pálya nagytengelye a két bolygópálya nagytengelyének számtani közepe, az időt pedig Kepler III. törvényéből kaphatjuk meg – ami szerint a bolygók \(\displaystyle T\) keringési idejének négyzete arányos a pályák \(\displaystyle a\) fél-nagytengelyének köbével: \(\displaystyle T=\alpha a^{3/2}\), ahol \(\displaystyle \alpha\) azonos a Nap körül keringő összes égitestre.
\(\displaystyle T_\mathrm{H}=\alpha a_\mathrm{H}^{3/2}=\alpha\left(\frac{1}{2}(R_\mathrm{F}+R_\mathrm{M})\right)^{3/2}=\alpha\left(\frac{1}{2}\left(\alpha^{-2/3}T_\mathrm{F}^{2/3}+\alpha^{-2/3}T_\mathrm{M}^{2/3}\right)\right)^{3/2}=\left(\frac{1}{2}\left(T_\mathrm{F}^{2/3}+T_\mathrm{M}^{2/3}\right)\right)^{3/2}=517{,}7\,\mathrm{nap}.\)
Az oda és a visszaút egyformán feleennyi, azaz 259 napig tart.
A Marson tartózkodás időtartamát jelöljük \(\displaystyle t\)-vel. A teljes űrutazás ideje alatt a Föld
\(\displaystyle \frac{t+T_\mathrm{H}}{T_\mathrm{F}}\)
fordulatot tesz meg a Nap körül (ez nem feltétlen egész szám, a Naphoz húzott vezérsugár ennyiszer 360\(\displaystyle ^\circ\)-ot fordul el). Ezalatt az űrhajósok az űrhajón és a Marson
\(\displaystyle \frac{1}{2}+\frac{t}{T_\mathrm{M}}+\frac{1}{2}\)
fordulatot tesznek meg a Nap körül. A két fordulat különbsége egész szám kell legyen, a Föld legalább eggyel több kört tesz meg:
\(\displaystyle \frac{t+T_\mathrm{H}}{T_\mathrm{F}}=1+\frac{t}{T_\mathrm{M}}+k\qquad k=1,2,3\ldots\)
ahonnan
\(\displaystyle t=\frac{T_\mathrm{M}\left((1+k)T_\mathrm{F}-T_\mathrm{H}\right)}{T_\mathrm{M}-T_\mathrm{F}}.\)
Az első alkalom visszaindulásra
\(\displaystyle t_1=\frac{687(2\cdot365{,}25-517{,}7)}{687-365{,}25}=454{,}4\)
nap után adódik, majd pedig \(\displaystyle T_\mathrm{sp}=\frac{T_\mathrm{F}T_\mathrm{M}}{T_\mathrm{M}-T_\mathrm{F}}=780\) naponként (az utóbbi időtartamot szinodikus periódusnak nevezik).
Megjegyzések. 1. A megadott ellipszispályát Hohmann-pályának nevezik Walter Hohmann német mérnök után, aki 1925-ben javasolta, mint rakétaüzemanyag-felhasználás szempontjából leggazdaságosabb bolygóközi pályát.
2. A Föld és a Mars pályájának numerikus excentricitása: 0,0167, illetve 0,0934. A Mars-pálya inklinációja (a pálya síkjának a Föld pályájáéval, vagyis az ekliptikával bezárt szöge): \(\displaystyle 1{,}85^\circ\). Ezeket a végső, pontosabb tervezéskor figyelembe kell venni.
Statisztika:
22 dolgozat érkezett. 5 pontot kapott: Beke Márton Csaba, Csiszár András, Elekes Panni, Klement Tamás, Kovács Tamás, Misik Balázs, Tóthpál-Demeter Márk. 4 pontot kapott: Bencze Mátyás, Ujpál Bálint, Ujvári Sarolta, Zólomy Csanád Zsolt. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2025. áprilisi fizika feladatai
