 |
A P. 5654. feladat (2025. május) |
P. 5654. Két, azonos hosszúságú, sűrűségű és keresztmetszetű, vékony fémrudat összeforrasztottunk, így egy kétszeres hosszúságú egyenes rudat kaptunk. Az egyik (A jelű) rész anyagának Young-modulusa \(\displaystyle E_{\mathrm{A}}\), a másik (B jelű) részé pedig \(\displaystyle {E_{\mathrm{B}}>E_{\mathrm{A}}}\). A rudat egy rá merőleges tengely körül adott nagyságú szögsebességgel megforgatjuk. A forgástengely
a) az A rúd szabad végpontján,
b) a B rúd szabad végpontján,
c) a forrasztási ponton
halad keresztül. A három eset közül melyikben lesz a teljes rúd megnyúlása a legnagyobb, illetve a legkisebb?
Közli: Holics László, Budapest
(4 pont)
A beküldési határidő 2025. június 16-án LEJÁRT.
Megoldás. A megforgatott rúd különböző részeiben különböző nagyságú húzófeszültség alakul ki, emiatt a rúd teljes megnyúlása csak az egyes (kicsiny) darabkái megnyúlásának összegzésével számítható ki. A feszültségeket mindhárom esetben a deformálatlan helyzetben számítjuk ki, majd ebből a feszültségből következtetünk a rúd kicsiny darabkáinak relatív hosszváltozására. Ez a közelítés azért alkalmazható, mert egy fémrúd rugalmas alakváltozása a szokásos húzófeszültségeknél nagyon kis mértékű, nagyon nagy feszültségeknél pedig az alakváltozás már nem követi a Hooke-törvényt. (A fenti közelítés nyilván nem lenne alkalmazható egy slinky-rugónál, vagy más ,,nagyon lágy'' rugóknál.)
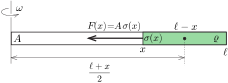
Tekintsük először a c) esetet, és számítsuk ki a rúd egyik felének megnyúlását. Jelöljük a félrúd hosszát \(\displaystyle \ell\)-lel, keresztmetszetét \(\displaystyle A\)-val, sűrűségét \(\displaystyle \varrho\)-val, a Young-modulusát \(\displaystyle E\)-vel, a forgás szögsebességét pedig \(\displaystyle \omega\)-val.
A rúdnak a forgástengelytől \(\displaystyle x\) távolságra lévő keresztmetszeténél fellépő \(\displaystyle F(x)\) erő a megforgatott rúd \(\displaystyle \ell-x\) hosszúságú, \(\displaystyle m=\varrho A(\ell-x)\) tömegű darabjának centripetális gyorsulását biztosítja (1. ábra). Mivel a kérdéses rúddarab tömegközéppontja \(\displaystyle r=\ell-\frac{\ell-x}{2}=\frac{\ell+x}{2}\) távol van a forgástengelytől, a mozgásegyenlet:
\(\displaystyle F(x)=mr\omega^2=\frac{1}{2}\varrho A\omega^2(\ell^2-x^2).\)
A húzófeszültség ezek szerint
\(\displaystyle \sigma(x)=\frac{F(x)}{A}=\frac{1}{2}\varrho\omega^2(\ell^2-x^2).\)
1. ábra
Osszuk fel – gondolatban – a rudat igen kicsi, \(\displaystyle \varDelta x\ll\ell\) hosszúságú darabokra, és egy-egy darabkán belül tekintsük a húzófeszültséget állandó, \(\displaystyle \sigma(x)\) nagyságúnak. A Hooke-törvény szerint egy-egy rúddarabka megnyúlása
\(\displaystyle \Delta s(x)=\frac{\sigma(x)}{E}\varDelta x,\)
a teljes (\(\displaystyle \ell\) hosszúságú) félrúd megnyúlása így
\(\displaystyle s=\sum\varDelta s(x)=\frac{\varrho\omega^2}{2E}\sum_{x=0}^\ell(\ell^2-x^2)\varDelta x.\)
Célszerű az \(\displaystyle x\) változót \(\displaystyle x=\xi\cdot\ell\) alakban felírni, ahol \(\displaystyle 0\le\xi\le 1\) egy dimenziótlan mennyiség. Nyilván \(\displaystyle \varDelta x=\ell\cdot\varDelta\xi\), és így
| \(\displaystyle (2)\) | \(\displaystyle s=\frac{\varrho\omega^2\ell^3}{2E}\sum_{\xi=0}^1(1-\xi^2)\varDelta\xi.\) |
A fenti összeg első tagja magától értetődő:
\(\displaystyle \sum_{\xi=0}^1 1\cdot\varDelta\xi=1.\)
A második tag már nem ennyire nyilvánvaló; kiszámítására három módszert is megadunk.
I. módszer. A kérdéses összeg egy határozott integrál annál jobb közelítése, minél kisebb darabokra osztottuk fel a félrudat:
\(\displaystyle \sum_{\xi=0}^1 \xi^2\,\varDelta\xi\approx\int_0^1\xi^2\,\mathrm{d}\xi=\left.\frac{\xi^3}{3}\right\vert_0^1=\frac{1}{3}.\)
II. módszer. Ha a félrudat \(\displaystyle n\gg 1\) számú (egyforma hosszúságú) darabra osztottuk fel, akkor a kérdéses összeg
\(\displaystyle \sum_{\xi=0}^1\xi^2\,\varDelta\xi\approx\sum_{k=1}^n\left(\frac{k}{n}\right)^2\,\frac1n=\frac{n(n+1)(2n+1)}{6n^3}=\frac{1}{6}\left(1+\frac{1}{n}\right)\left(2+\frac{1}{n}\right)\approx\frac{1}{3}.\)
III. módszer. Tekintsünk egy derékszögű, egyenlő szárú háromszög alakú lemezt, amelynek felületegységre jutó súlya éppen 1. Ha a lemez függőleges síkban helyezkedik el úgy, hogy a háromszög egyik (egységnyi hosszúságú) szára vízszintes és a csúcsa az origóban van (lásd a 2. ábrát), akkor a nehézségi erő \(\displaystyle M\) forgatónyomatéka az \(\displaystyle O\) csúcsra éppen a keresett szummával egyenlő. (Ha ugyanis a lemezt – gondolatban - sok keskeny csíkra vágjuk, akkor az egyes csíkok területe, vagyis a tömege \(\displaystyle \xi\cdot\varDelta\xi\), az erőkar, azaz a csúcstól vízszintesen mért távolság pedig ugyancsak \(\displaystyle \xi\) nagyságú.)

2. ábra
\(\displaystyle M\approx\sum_{\xi=0}^1\xi\cdot(\xi\,\varDelta\xi).\)
Ugyanezt a forgatónyomatékot úgy is megkaphatjuk, hogy a háromszög súlyát (ami a területével, vagyis \(\displaystyle 1/2\)-del egyezik meg) megszorozzuk az erőkarral, azaz a súlyponton átmenő függőleges egyenes és a csúcs \(\displaystyle 2/3\) egységnyi távolságával:
\(\displaystyle M=\frac{1}{2}\cdot\frac{2}{3}=\frac{1}{3}.\)
A fentiek szerint
\(\displaystyle \sum_{\xi=0}^1(1-\xi^2)\varDelta\xi=1-\frac{1}{3}=\frac{2}{3},\)
és így (2) felhasználásával a teljes (\(\displaystyle 2\ell\) hosszúságú) rúd megnyúlása a c) esetben:
| \(\displaystyle (3c)\) | \(\displaystyle s_\mathrm{c}=\frac{\varrho\omega^2\ell^3}{3}\left(\frac{1}{E_\mathrm{A}}+\frac{1}{E_\mathrm{B}}\right)=\frac{\varrho\omega^2\ell^3}{6E_\mathrm{A}E_\mathrm{B}}\left(2{E_\mathrm{A}}+2{E_\mathrm{B}}\right).\) |
Számítsuk ki most a \(\displaystyle 2\ell\) hosszúságú rúd megnyúlását, ha a rudat az A rúd végpontja körül forgatjuk \(\displaystyle \omega\) szögsebességgel. A húzófeszültség ebben az esetben a forgástengelytől \(\displaystyle x\) távolságban
\(\displaystyle \sigma(x)=\frac{1}{2}\varrho\omega^2(4\ell^2-x^2),\)
a megnyúlás pedig (a rúd két felének különböző Young-modulusával számolva)
\(\displaystyle s_\mathrm{a}=\frac{\varrho\omega^2}{2}\left(\frac{1}{E_\mathrm{A}}\sum_{x=0}^\ell(4\ell^2-x^2)\varDelta x+\frac{1}{E_\mathrm{B}}\sum_{x=\ell}^{2\ell}(4\ell^2-x^2)\varDelta x\right).\)
Célszerű bevezetni az \(\displaystyle x=2\ell\cdot\xi\) jelölést (\(\displaystyle 0\le\xi\le 1\)), amellyel a megnyúlás így írható:
\(\displaystyle s_\mathrm{a}=4\varrho\omega^2\ell^3\left(\frac{1}{E_\mathrm{A}}\sum_{\xi=0}^{1/2}(1-\xi^2)\varDelta\xi+\frac{1}{E_\mathrm{B}}\sum_{\xi=1/2}^{1}(1-\xi^2)\varDelta\xi\right).\)
Az itt szereplő összegeket a korábban alkalmazott három módszer bármelyikével ki tudjuk számítani, és az eredmény:
\(\displaystyle \sum_{\xi=0}^{1/2}(1-\xi^2)\varDelta\xi=\frac{11}{24},\qquad\text{illetve}\qquad\sum_{\xi=1/2}^{1}(1-\xi^2)\varDelta\xi=\frac{5}{24}.\)
Ennek megfelelően a rúd megnyúlása az a) esetben
| \(\displaystyle (3a)\) | \(\displaystyle s_\mathrm{a}=\frac{\varrho\omega^2\ell^3}{6}\left(\frac{11}{E_\mathrm{A}}+\frac{5}{E_\mathrm{B}}\right)=\frac{\varrho\omega^2\ell^3}{6E_\mathrm{A}E_\mathrm{B}}\left(5{E_\mathrm{A}}+11{E_\mathrm{B}}\right).\) |
Ebből \(\displaystyle E_\mathrm{A}\) és \(\displaystyle E_\mathrm{B}\) felcserélésével megkapjuk a b) esethez tartozó megnyúlást is:
| \(\displaystyle (3b)\) | \(\displaystyle s_\mathrm{b}=\frac{\varrho\omega^2\ell^3}{6E_\mathrm{A}E_\mathrm{B}}\left(11{E_\mathrm{A}}+5{E_\mathrm{B}}\right).\) |
A három megnyúlás összehasonlításához elegendő a (3a), (3b) és (3c) képletekben szereplő zárójeles kifejezéseket összevetnünk, hiszen az előttük álló szorzótényezők megegyeznek. Nyilván \(\displaystyle s_\mathrm{a}>s_\mathrm{b}\), mert \(\displaystyle E_\mathrm{B}>E_\mathrm{A}\) esetén
\(\displaystyle \left(11{E_\mathrm{B}}+5{E_\mathrm{A}}\right)-\left(11{E_\mathrm{A}}+5{E_\mathrm{B}}\right)=7\left(E_\mathrm{B}-E_\mathrm{A}\right)>0,\)
és \(\displaystyle s_\mathrm{b}>s_\mathrm{c}\) is teljesül, hiszen \(\displaystyle E_\mathrm{A}>0\) és \(\displaystyle E_\mathrm{B}>0\).
A rúd teljes megnyúlása tehát az a) esetben lesz a legnagyobb és a c) esetben a legkisebb.
Statisztika:
11 dolgozat érkezett. 3 pontot kapott: Vincze Anna, Zólomy Csanád Zsolt. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2025. májusi fizika feladatai
