 |
A P. 5655. feladat (2025. május) |
P. 5655. Két, egymástól \(\displaystyle d\) távolságra lévő egyforma hangforrás azonos fázisban \(\displaystyle \lambda\) hullámhosszúságú hanghullámot sugároz ki, amit egy vevő egy \(\displaystyle R\) sugarú kör egy pontjában detektál. A két hangforrás a kör középpontjához képest szimmetrikusan helyezkedik el. Hol vannak azok a pontok, ahol a két hangforrás hulláma maximálisan erősíti egymást, ha \(\displaystyle d=2\lambda\) és \(\displaystyle R\gg d\)?
Közli: Cserti József, Budapest
(4 pont)
A beküldési határidő 2025. június 16-án LEJÁRT.
Megoldás. Maximális erősítés azokban a pontokban van, ahova a két forrásból érkező hullámok azonos fázisban érkeznek, azaz a két út különbsége a hullámhossz egész számú többszöröse.
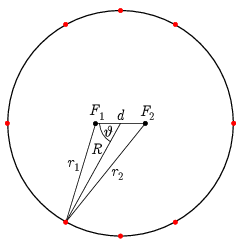
Az ábra jelöléseivel
\(\displaystyle r_1-r_2=n\lambda,\)
azaz, az \(\displaystyle r\)-eket a koszinusz tétel segítségével kifejezve
\(\displaystyle \sqrt{R^2+\left(\frac{d}{2}\right)^2-Rd\cos\vartheta}-\sqrt{R^2+\left(\frac{d}{2}\right)^2+Rd\cos\vartheta}=n\lambda.\)
Ebből jól megválasztott négyzetre emelések után a \(\displaystyle \cos\vartheta\) kifejezhető:
\(\displaystyle \cos\vartheta=\sqrt{1+\left(\frac{d}{2R}\right)^2-\left(\frac{n\lambda}{2R}\right)^2}\left(\frac{n\lambda}{d}\right).\)
Feladatunkban \(\displaystyle R\gg d,\lambda\), tehát a négyzetgyök alatti törtek jó közelítéssel elhagyhatók az egy mellett, így
\(\displaystyle \cos\vartheta\cong\frac{n\lambda}{d}.\)
Ennek \(\displaystyle \vartheta\)-ra a \(\displaystyle \lambda/d=1/2\) miatt csak \(\displaystyle n=0,\,\pm 1\,\textrm{és}\,\pm 2\) mellett van megoldása. A lehetséges szögek (irányok) tehát \(\displaystyle \vartheta=0,\,\pm\pi/3,\,\pm\pi/2,\,\pm 2\pi/3\,\textrm{és}\,\pi\). A megfelelő pontokat az ábrán piros körökkel jelöltük.
Megjegyzés. Az első egyenletünkkel azonos szerkezetű \(\displaystyle \left|r_1-r_2\right|=2a\) egyenletek olyan hiperbolákat határoznak meg, amelyek két fókuszpontja a két hangforrás (\(\displaystyle F_1\) és \(\displaystyle F_2\)), azaz \(\displaystyle d=2c\). Általános \(\displaystyle R\) mellett a keresett pontok az \(\displaystyle a=n\lambda/2\)-vel megadható hiperbolák és a kör metszéspontjai. \(\displaystyle R\gg c\) esetén a hiperbolák a végérintőikkel helyettesíthetők. Esetünkben csak az \(\displaystyle n=\pm 1\) által meghatározott (\(\displaystyle a=c/2\) valós tengelyű) hiperbola-pár ,,normális", az \(\displaystyle n=0\)-hoz, és az \(\displaystyle n=\pm 2\)-höz tartozó hiperbolák, amikor is \(\displaystyle a=0\) illetve \(\displaystyle a=c\), elfajultak.
Statisztika:
17 dolgozat érkezett. 4 pontot kapott: Bélteki Teó, Blaskovics Ádám, Fekete Lúcia, Klement Tamás, Molnár Lili, Ujpál Bálint. 3 pontot kapott: Pituk Péter, Varga 802 Zsolt, Vértesi Janka, Zámbó Luca. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2025. májusi fizika feladatai
