A P. 5656. feladat (2025. május)

P. 5656. Végtelen ellenállásláncot készítünk a következő módon: Az első ,,lépcső'' ellenállásainak értéke \(\displaystyle R\), a következőké \(\displaystyle 2R\), \(\displaystyle 4R\), \(\displaystyle \ldots\) stb., mindig kétszerese az előzőnek (ábra). Mekkora a végtelen ellenálláslánc eredő ellenállása?

Közli: Szentivánszki Soma, Budapest

(4 pont)

A beküldési határidő 2025. június 16-án LEJÁRT.

Megoldás. Ha az első ,,lépcsőt'' elhagynánk, akkor egy ugyanolyan végtelen ellenállásláncot kapnánk, mint az eredeti, csak minden ellenállás értéke az eredeti kétszerese lenne, és így az eredő ellenállása is az eredeti lánc (keresett) \(\displaystyle R_\mathrm{e}\) eredő ellenállásának kétszerese lenne (ábra a) része). Ez alapján az eredeti láncot az ábra b) részén látható módon átrajzolhatjuk.

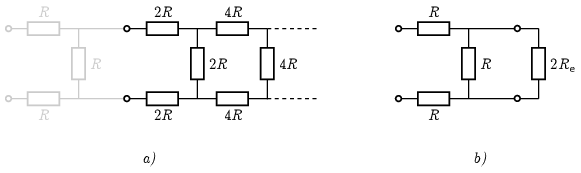
Ebből az eredő ellenállásra a következő egyenletet kapjuk:

\(\displaystyle R_\mathrm{e}=2R+R\times 2R_\mathrm{e}=2R+\frac{2RR_\mathrm{e}}{R+2R_\mathrm{e}}.\)

(Itt \(\displaystyle \times\) a ,,replusz'' jele: a reciprokok összegének reciproka.) Az egyenletet rendezve:

\(\displaystyle 2R_\mathrm{e}^2-5RR_\mathrm{e}-2R^2=0,\)

amelynek pozitív megoldása:

\(\displaystyle R_\mathrm{e}=\frac{5+\sqrt{41}}{4}R\approx 2{,}85 R.\)

Statisztika:

15 dolgozat érkezett.
4 pontot kapott:	Bélteki Teó, Csipkó Hanga Zoé , Csiszár András, Erdélyi Dominik, Hasulyó Dorián, Sipos Márton, Vértesi Janka, Vincze Anna.
3 pontot kapott:	Blaskovics Ádám.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2025. májusi fizika feladatai