 |
A P. 5659. feladat (2025. május) |
P. 5659. Maghasadásos reakciókban gyakran keletkezik \(\displaystyle ^{92}\mathrm{Sr}\) izotóp, amely két egymást követő \(\displaystyle \beta\)-bomlással a stabil \(\displaystyle ^{92}\mathrm{Zr}\)-ra bomlik:
\(\displaystyle {}^{92}\mathrm{Sr}~\xrightarrow{2{,}66~\mathrm{h}}~{}^{92}\mathrm{Y}~\xrightarrow{3{,}54~\mathrm{h}}~{}^{92}\mathrm{Zr}. \)
Egy adag vegytiszta \(\displaystyle ^{92}\mathrm{Sr}\) preparátum elkészítése után mennyi idővel lesz a keletkező \(\displaystyle ^{92}\mathrm{Y}\) mennyisége a legnagyobb?
Útmutatás: Próbálhatjuk az egyenleteket egyetlen radioaktív bomlási egyenletre visszavezetni. Ötletet adhat a következő kétrészes cikk: Vigh Máté: Összetett rezgések I–II. (https://www.komal.hu/cikkek/cikklista.h.shtml)
Közli: Vigh Máté, Herceghalom
(5 pont)
A beküldési határidő 2025. június 16-án LEJÁRT.
I. megoldás. Jelöljük a stroncium (Sr) magok számát a \(\displaystyle t\) időpillanatban \(\displaystyle N_1\)-gyel, az ittrium (Y) magok számát pedig \(\displaystyle N_2\)-vel. Ekkor az egyes magok számának változási sebessége:
$$\begin{gather*} \frac{\Delta N_1}{\Delta t}=-\lambda_1N_1,\tag{1}\\ \frac{\Delta N_2}{\Delta t}=\lambda_1N_1-\lambda_2N_2,\tag{2} \end{gather*}$$ahol \(\displaystyle \lambda_1=\tfrac{\ln 2}{T_1}\) és \(\displaystyle \lambda_2=\tfrac{\ln 2}{T_2}\) a két folyamat bomlási állandója, \(\displaystyle T_1=2{,}66\,\textrm{h}\) és \(\displaystyle T_2=3{,}54\,\textrm{h}\) pedig a két folyamat felezési ideje. Az első egyenlet a jól ismert bomlási törvény: stroncium magok nem keletkeznek, csak bomlanak \(\displaystyle T_1\) felezési idővel. A második egyenlet bonyolultabb, hiszen ittrium magok keletkeznek és bomlanak is: egyrészt időegységenként annyi mag keletkezik, ahány stroncium mag elbomlik (első tag), másrészt a bomlási törvény szerint \(\displaystyle T_2\) felezési idővel bomlik, és ezzel csökken a magok száma (második tag).
Az (1) egyenlet megoldását jól ismerjük:
| \(\displaystyle (3)\) | \(\displaystyle N_1=N_0\mathrm{e}^{-\lambda_1 t},\) |
ahol \(\displaystyle N_0\) a stroncium magok száma a \(\displaystyle t=0\) időpillanatban. Nekünk viszont \(\displaystyle N_2\) időfüggvényére van szükségünk, de a (2) egyenlet bonyolultabb, hiszen \(\displaystyle N_2\)-n kívül \(\displaystyle N_1\)-et is tartalmazza. A megoldáshoz használjuk a feladatban ajánlott cikk módszerét: keressük az \(\displaystyle N_1\) és \(\displaystyle N_2\) mennyiségek olyan lineáris kombinációját (tehát egy \(\displaystyle N=a_1N_1+a_2N_2\) mennyiséget, ahol \(\displaystyle a_1\) és \(\displaystyle a_2\) állandók), amelyre a jól ismert
\(\displaystyle \frac{\Delta N}{\Delta t}=-\lambda N\)
bomlási törvényt írhatjuk fel. Az \(\displaystyle a_1\) és \(\displaystyle a_2\) együtthatók meghatározásához helyettesítsük be az eredeti egyenleteinket:
\(\displaystyle \frac{\Delta N}{\Delta t}=a_1\frac{\Delta N_1}{\Delta t}+a_2\frac{\Delta N_2}{\Delta t}=-a_1\lambda_1N_1+a_2(\lambda_1N_1-\lambda_2N_2)=-\lambda N=-\lambda(a_1N_1+a_2N_2).\)
Ennek minden \(\displaystyle N_1\) és \(\displaystyle N_2\)-re teljesülni kell, amiből:
$$\begin{gather*} -(a_1-a_2)\lambda_1=-a_1\lambda,\\ -a_2\lambda_2=-a_2\lambda. \end{gather*}$$Ebből egyrészt \(\displaystyle \lambda=\lambda_2\), másrészt \(\displaystyle a_1(\lambda_1-\lambda_2)=a_2\lambda_1\), azaz választhatjuk például az \(\displaystyle a_1=\lambda_1\) és \(\displaystyle a_2=\lambda_1-\lambda_2\) állandókat. Így \(\displaystyle N=\lambda_1N_1+(\lambda_1-\lambda_2)N_2\), az egyenletünk pedig:
\(\displaystyle \frac{\Delta N}{\Delta t}=-\lambda_2N.\)
Ennek megoldása már ismét jól ismert:
| \(\displaystyle (4)\) | \(\displaystyle N=\lambda_1N_0\mathrm{e}^{-\lambda_2 t},\) |
ahol kihasználtuk, hogy a \(\displaystyle t=0\) pillanatban csak stroncium magok vannak, így \(\displaystyle N(0)=\lambda_1N_0\). Ezután \(\displaystyle N_1\) és \(\displaystyle N\) ismeretében a (3) és (4) időfüggvényekből már \(\displaystyle N_2\) is kifejezhető:
| \(\displaystyle (5)\) | \(\displaystyle N_2=\frac{N-\lambda_1N_1}{\lambda_1-\lambda_2}=\frac{\lambda_1N_0}{\lambda_1-\lambda_2}\left(\mathrm{e}^{-\lambda_2 t}-\mathrm{e}^{-\lambda_1 t}\right).\) |
A függvény értéke a \(\displaystyle t=0\) pillanatban és \(\displaystyle t\to\infty\) is nulla, kezdetben növekszik, majd csökken. Maximuma abban a \(\displaystyle t^\star\) időpontban lesz, ahol a változási sebessége éppen nulla, így (2), (3) és (5) alapján:
\(\displaystyle \frac{\Delta N_2}{\Delta t}=\lambda_1N_1-\lambda_2N_2=\lambda_1N_0\mathrm{e}^{-\lambda_1 t^\star}-\frac{\lambda_1\lambda_2N_0}{\lambda_1-\lambda_2}\left(\mathrm{e}^{-\lambda_2 t^\star}-\mathrm{e}^{-\lambda_1 t^\star}\right)=0.\)
Rendezve, majd mindkét oldal természetes alapú logaritmusát véve, és tovább rendezve a keresett időpont:
$$\begin{gather*} \lambda_1\mathrm{e}^{-\lambda_1t^\star}=\lambda_2\mathrm{e}^{-\lambda_2t^\star},\\ \ln\lambda_1-\lambda_1t^\star=\ln\lambda_2-\lambda_2t^\star,\\ t^*=\frac{1}{\lambda_1-\lambda_2}\ln\left(\frac{\lambda_1}{\lambda_2}\right)=\frac{1}{\ln 2}\frac{T_1T_2}{T_2-T_1}\ln\left(\frac{T_2}{T_1}\right)\approx 4{,}41\,\textrm{óra}. \end{gather*}$$Megjegyzések. 1. \(\displaystyle N_2\) maximális értéke \(\displaystyle t^\star\) (5)-be való behelyettesítésével megkapható:
\(\displaystyle N_2(t^\star)=\frac{\lambda_1}{\lambda_1-\lambda_2}\left(\left(\frac{\lambda_1}{\lambda_2}\right)^\frac{\lambda_2}{\lambda_2-\lambda_1}-\left(\frac{\lambda_1}{\lambda_2}\right)^\frac{\lambda_1}{\lambda_2-\lambda_1}\right)N_0=\frac{T_2}{T_2-T_1}\left(\left(\frac{T_2}{T_1}\right)^\frac{T_1}{T_1-T_2}-\left(\frac{T_2}{T_1}\right)^\frac{T_2}{T_1-T_2}\right)N_0\approx 0{,}422 N_0.\)
2. \(\displaystyle N_2\) szélsőértéke \(\displaystyle N_2\) ismeretében deriválással is meghatározható.
3. Érdekes megnézni a \(\displaystyle \lambda_1=\lambda_2=\lambda\) esetet. Ilyenkor az (5) függvényben egy \(\displaystyle \tfrac{0}{0}\) tényező jelenne meg. A megoldás ebben az esetben \(\displaystyle N_2=\lambda tN_0\mathrm{e}^{-\lambda t}\) és \(\displaystyle t^\star=\tfrac{1}{\ln 2}T\).
II. megoldás. A feladat numerikusan is megoldható. Ehhez lásd Csóka Péter, Seprődi Barnabás: Fizika problémák megoldása numerikus módszerekkel cikkét a KöMaL 2024. novemberi számában.
Használjuk az I. megoldás jelöléseit, és az (1) és (2) összefüggéseket. A programunk változói \(\displaystyle t\), \(\displaystyle N_1\) és \(\displaystyle N_2\), paraméterei \(\displaystyle \lambda_1=\tfrac{\ln 2}{T_1}\), \(\displaystyle \lambda_2=\tfrac{\ln 2}{T_2}\) és \(\displaystyle \Delta t\) (a közelítő számítás ,,felbontása''). Legyen \(\displaystyle N_0=1\) (így \(\displaystyle N_1\) és \(\displaystyle N_2\) relatív értékek lesznek a kiinduló mennyiséghez képest.)
A paramétereink kezdőértéke legyen:
$$\begin{gather*} t:=0,\\ N_1:=1,\\ N_2:=0. \end{gather*}$$Ezután ismételjük a következő ciklust:
$$\begin{gather*} t:=t+\Delta t,\\ N_2:=N_2+(\lambda_1N_1-\lambda_2N_2)\Delta t,\\ N_1:=N_1-\lambda_1N_1\Delta t, \end{gather*}$$mindaddig, amíg \(\displaystyle \lambda_1N_1-\lambda_2N_2>0\). Amikor ez az érték előjelet vált, állítsuk le a ciklust, és írjuk ki \(\displaystyle t\) értékét.
A ciklust tovább futtatva, és az adatokat ábrázolva elkészíthetjük az \(\displaystyle N_1(t)\) és \(\displaystyle N_2(t)\) grafikonokat is. Az ábrán látható grafikonon a cirkónium (Zr) magok \(\displaystyle N_3(t)\) relatív értékét is ábrázoltuk, amely az \(\displaystyle N_3=N_0-(N_1+N_2)\) képlettel minden időpontban könnyen meghatározható.
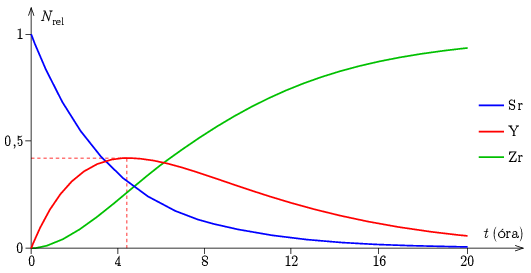
Megjegyzés. A futtatáshoz bármilyen program használható, de elvégezhető akár Excel táblázatkezelővel is: ekkor a képleteket az első sorba beírva autokitöltővel lehet a sorokat létrehozni, majd grafikonvarázslóval a grafikont elkészíteni. Az ábra is így készült \(\displaystyle \Delta t=0{,}01\,\textrm{óra}\) lépéssel.
Statisztika:
16 dolgozat érkezett. 5 pontot kapott: Beke Márton Csaba, Erdélyi Dominik, Gyenes Károly, Hasulyó Dorián, Simon János Dániel, Sipos Márton, Tóthpál-Demeter Márk, Zólomy Csanád Zsolt. 4 pontot kapott: Papp Emese Petra, Páternoszter Tamás. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2025. májusi fizika feladatai
