 |
A P. 5660. feladat (2025. május) |
P. 5660. Egy pontszerűnek tekinthető, \(\displaystyle m\) tömegű, átfúrt golyó az ábra szerint egy \(\displaystyle R\) sugarú, vízszintes átmérőjű, függőleges síkú, félkör alakú, rögzített, merev drótra van fűzve, amelyen súrlódásmentesen csúszhat. A golyóhoz egy vékony fonál van kötve, amely a drót \(\displaystyle C\) végén lévő, kicsiny csigán van átvetve. A fonál másik végéhez egy ugyancsak \(\displaystyle m\) tömegű nehezék van erősítve. A bal oldali golyót a fonál vízszintes helyzetéből lökésmentesen elengedjük, amikor a fonál \(\displaystyle \alpha=0^\circ\)-os szöget zár be a vízszintes átmérővel.
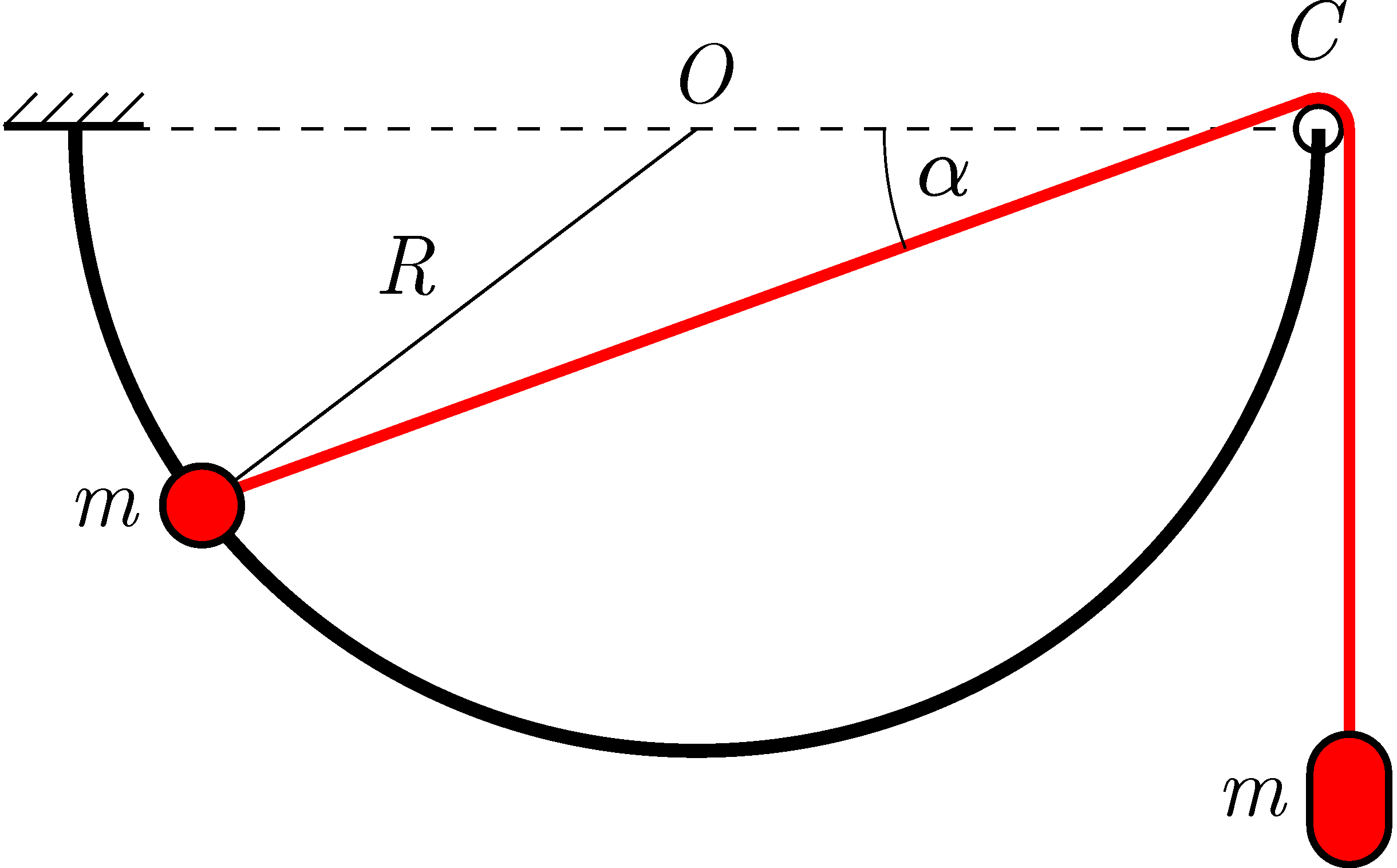
a) Mekkora sebességgel mozognak a testek, amikor a bal oldali test a drótpálya legalsó pontján halad át?
b) Mekkora a testek gyorsulása ebben a pillanatban?
Közli: Zsigri Ferenc, Budapest
(6 pont)
A beküldési határidő 2025. június 16-án LEJÁRT.
Megoldás. a) Amikor a bal oldali test a drótpálya legalsó pontján halad át, akkor \(\displaystyle \alpha=45^\circ\). Legyen ebben a pillanatban a bal oldali test sebessége \(\displaystyle v\), és így a kényszerfeltétel (vagyis az állandó fonálhossz miatt) a jobb oldali test sebessége \(\displaystyle \tfrac{v}{\sqrt{2}}\). Ezeket a sebességeket a munkatételből (vagy az energiamegmaradásból) kaphatjuk meg:
\(\displaystyle mgR+mg\left(2-\sqrt{2}\right)R=\frac{1}{2}mv^2+\frac{1}{2}m\left(\frac{v}{\sqrt2}\right)^2,\)
amiből
\(\displaystyle v_{\mathrm{bal}}=v=\sqrt{\frac{4(3-\sqrt{2})}{3}gR}\qquad\textrm{és}\qquad v_{\mathrm{jobb}}=\frac{v}{\sqrt{2}}=\sqrt{\frac{2(3-\sqrt{2})}{3}gR}.\)
b) Vizsgáljunk egy általános esetet, amikor a bal oldali test valamilyen \(\displaystyle \alpha\) szöggel fordult el. Ebben a helyzetben a bal oldali test sebessége legyen \(\displaystyle v_{\mathrm{b}}\), és a kötél hosszának állandósága miatt a jobb oldali test sebessége:
\(\displaystyle v_{\mathrm{j}}=v_{\mathrm{b}}\cdot \sin{\alpha}, \)
amint azt az 1. ábráról leolvashatjuk. Azt is megállapíthatjuk, hogy az \(\displaystyle OP\) egyenes ebben a helyzetben éppen
\(\displaystyle \omega=\frac{v_{\mathrm{b}}}{R}\)
szögsebességgel forog. A fonál ferde részének, vagyis a \(\displaystyle CP\) egyenesnek a forgási szögsebessége \(\displaystyle \omega/2\), hiszen a vízszintessel bezárt szöge csak fele akkora, mint az \(\displaystyle OP\) sugár hajlásszöge.

1. ábra
A továbbiakban szükségünk lesz a bal és a jobb oldali test gyorsulása közötti kapcsolatra. Ezt kétféle módszerrel is meghatározhatjuk. A bal oldali test gyorsulásvektorának \(\displaystyle OP\) irányú (centripetális) komponense nyilván
\(\displaystyle a_\mathrm{cp}^{(O)}=\frac{v_\mathrm{b}^2}{R}.\)
Az \(\displaystyle (O)\) jel arra figyelmeztet, hogy az \(\displaystyle O\) pont körüli elfordulásból származó centripetális gyorsulásról van szó.
Az \(\displaystyle OP\) egyenesre merőleges (érintő irányú) gyorsuláskomponens a \(\displaystyle v_{\mathrm{b}}\) sebességnagyság növekedési üteméből származik, ezt \(\displaystyle a_{\mathrm{b}}\)-vel jelöljük. A 2. ábrán ezeket az összetevőket kék nyilakkal ábrázoltuk.
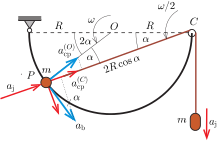
2. ábra
Ugyanez a gyorsulásvektor felbontható \(\displaystyle CP\) irányú és arra merőleges összetevőkre. A \(\displaystyle CP\) irányú gyorsuláskomponens egyrészt az \(\displaystyle CP\) fonálhossz gyorsuló ütemű rövidüléséből származik, ami megegyezik a jobb oldali test függőleges irányú \(\displaystyle a_{\mathrm{j}}\) gyorsulásával, másrészt a \(\displaystyle CP=2R\cos\alpha\) hosszúságú szakasz \(\displaystyle \omega/2\) szögsebességű forgásából adódik. (Ez utóbbi is centripetális gyorsulás, de az most nem az \(\displaystyle O\) pontra, hanem a \(\displaystyle C\) pontra vonatkozik.) Ez a komponens \(\displaystyle CP=2R\cos\alpha\) hosszúságú szakasz \(\displaystyle \omega/2=\frac{v_{\mathrm{b}}}{2R}\) szögsebességű forgásából származik, nagysága tehát
\(\displaystyle a_\mathrm{cp}^{(C)}=2R\cos\alpha \left(\frac{v_{\mathrm{b}}}{2R}\right)^2\)
A \(\displaystyle P\) pont gyorsulásának van \(\displaystyle CP\)-re merőleges, tehát a \(\displaystyle C\) körüli forgás szempontjából tangenciális komponense, de ennek nagyságát nem szükséges meghatároznunk. A \(\displaystyle C\) pontra vonatkoztatott gyorsuláskomponenseket a 2. ábrán piros nyilak szemléltetik.
A kék gyorsulásvektorok összege, és így annak \(\displaystyle CP\) irányú vetülete megegyezik a piros gyorsulásvektorok összegével, illetve annak \(\displaystyle CP\) irányú vetületével.
\(\displaystyle a_{\mathrm{b}} \,\sin\alpha+\cos\alpha\frac{v_\mathrm{b}^2}{R}=a_{\mathrm{j}}+2R\cos\alpha \left(\frac{v_{\mathrm{b}}}{2R}\right)^2,\)
ahonnan
\(\displaystyle a_{\mathrm{j}}=a_{\mathrm{b}} \,\sin\alpha+\cos\alpha\frac{{v_{\mathrm{b}}^2}}{2R}.\)
A gyorsulások közötti összefüggést más módon, a differenciálszámítás összefüggéseinek alkalmazásával is levezethetjük. A bal oldali test pályamenti (érintőirányú) gyorsulása \(\displaystyle a_{\mathrm{b}}=\frac{\mathrm{d} v_{\mathrm{b}}}{\mathrm{d} t}\). A jobb oldali test gyorsulását a szorzatfüggvény deriválási szabálya szerint kaphatjuk meg:
\(\displaystyle a_{\mathrm{j}}=\frac{\mathrm{d} v_{\mathrm{j}}}{\mathrm{d} t}=\frac{\mathrm{d} (v_{\mathrm{b}}\cdot \sin{\alpha})}{\mathrm{d} t}=a_{\mathrm{b}}\cdot \sin{\alpha}+v_{\mathrm{b}}\cdot\cos{\alpha}\cdot\frac{\mathrm{d} \alpha}{\mathrm{d} t}=a_{\mathrm{b}}\cdot \sin{\alpha}+v_{\mathrm{b}}\cdot\cos{\alpha}\cdot(\omega/2)=\)
\(\displaystyle =a_{\mathrm{b}}\cdot \sin{\alpha}+v_{\mathrm{b}}\cdot\cos{\alpha}\cdot\frac{v_{\mathrm{b}}\cdot\cos{\alpha}}{2R\cos{\alpha}}=a_{\mathrm{b}}\cdot \sin{\alpha}+\cos{\alpha}\cdot\frac{{v_{\mathrm{b}}^2}}{2R}.\)
Ezek után térjünk át az \(\displaystyle \alpha=45^\circ\)-os helyzetre:
\(\displaystyle a_{\mathrm{jobb}}=a_{\mathrm{bal}}\cdot \sin{45^\circ}+\cos{45^\circ}\cdot\frac{{v_{\mathrm{bal}}^2}}{2R}=\frac{a_{\mathrm{bal}}}{\sqrt 2}+\frac{{v_{\mathrm{bal}}^2}}{2\sqrt2R}.\)
A fonálban ébredő feszítőerő legyen \(\displaystyle F\). A jobb oldali testre ezt a dinamikai egyenletet írhatjuk fel:
\(\displaystyle mg-F=ma_{\mathrm{jobb}}=m\left(\frac{a_{\mathrm{bal}}}{\sqrt 2}+\frac{{v_{\mathrm{bal}}^2}}{2\sqrt2R}\right).\)
Hasonló módon a bal oldali test pályamenti gyorsulására felírható mozgásegyenlet:
\(\displaystyle \frac{F}{\sqrt{2}}=ma_\mathrm{bal}.\)
A fenti két egyenletből
\(\displaystyle F=\frac{10-6\sqrt{2}}{9}mg\approx0{,}168\,mg\qquad\mathrm{és}\qquad a_{\mathrm{bal}}=\frac{5\sqrt{2}-6}{9}g\approx 0{,}119\,g,\qquad\mathrm{illetve} \qquad a_{\mathrm{jobb}}=\frac{6\sqrt{2}-1}{9}g\approx 0{,}832\,g.\)
Ezzel megkaptuk a jobb oldali test gyorsulását, azonban \(\displaystyle a_{\mathrm{bal}}\) csak a pályamenti (érintőleges) gyorsulást jelenti.
A bal oldali test gyorsulása két összetevőre bontható; a fenti pályamenti (érintőleges) gyorsulásra és a sugárirányú centripetális gyorsulásra: \(\displaystyle a_\mathrm{cp}=\frac{{v_{\mathrm{bal}}^2}}{R}=\frac{4(3-\sqrt{2})}{3}g\approx 2{,}11\,g\). A bal oldali test eredő gyorsulását Pitagorasz-tétellel számíthatjuk ki:
\(\displaystyle {a_\mathrm{bal}}^{\mathbf{eredő}}=\sqrt{{a_{\mathrm{bal}}}^2+{a_\mathrm{cp}}^2}=\frac{\sqrt{1670-924\sqrt{2}}}{9}g\approx 2{,}12\,g.\)
Statisztika:
15 dolgozat érkezett. 6 pontot kapott: Beke Márton Csaba, Erdélyi Dominik, Ujvári Sarolta. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2025. májusi fizika feladatai
