A P. 5670. feladat (2025. október)

P. 5670. Két, egymást merőlegesen keresztező úton egy-egy motoros halad. Az egyik sebessége \(\displaystyle v_1\), a másiké \(\displaystyle v_2\), és az egymástól való legkisebb távolságuk \(\displaystyle d_0\). Milyen távolságra vannak ekkor a kereszteződéstől?

Az egyszerűség kedvéért mindkét járművet tekintsük pontszerűnek.

Közli: Woynarovich Ferenc, Budapest

(5 pont)

A beküldési határidő 2025. november 17-én LEJÁRT.

I. megoldás. Vázoljuk azt a helyzetet, amikor a két motoros közötti távolság éppen a minimális \(\displaystyle d_0\). Amikor mindkét motoros közeledik a kereszteződéshez, vagy már távolodik attól, a távolságuk egyértelműen csökken, illetve nő, tehát a kérdéses pillanatban az egyik még nem, de a másik már elhagyta a kereszteződést. Jelöljük a pozíciójukat \(\displaystyle A\)-val és \(\displaystyle B\)-vel, legyen a távolságuk az \(\displaystyle O\)-val jelölt kereszteződéstől rendre \(\displaystyle d_1\) illetve \(\displaystyle d_2\), és legyen \(\displaystyle BAO\sphericalangle=\alpha\), ahogy azt az 1. ábra a) része mutatja.

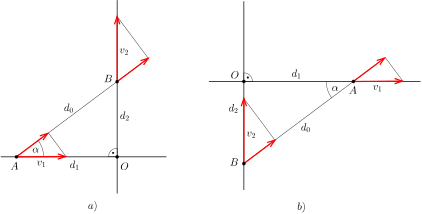
1. ábra

Az \(\displaystyle A\) és a \(\displaystyle B\) pont éppen sem nem közeledik, sem nem távolodik egymástól, tehát a sebességük \(\displaystyle AB\)-vel párhuzamos komponense egyenlő:

\(\displaystyle v_1\cos\alpha=v_2\sin\alpha,\)

azaz

\(\displaystyle \tg\alpha=\frac{v_1}{v_2}.\)

Ennek megfelelően

\(\displaystyle d_1=d_0\cos\alpha=d_0\frac{v_2}{\sqrt{v_1^2+v_2^2}}\qquad\textrm{és}\qquad d_2=d_0\sin\alpha=d_0\frac{v_1}{\sqrt{v_1^2+v_2^2}}.\)

Természetesen az is lehetséges, hogy az eddigi feltételezésünkkel szemben a \(\displaystyle v_1\) sebességű motor hagyta már el a kereszteződést, és a \(\displaystyle v_2\) sebességű az, amelyik csak közeledik hozzá, ahogy azt az 1. ábra b) része mutatja, de a kérdéses távolságok ebben az esetben is ugyanakkorák.

II. megoldás. Használjuk az I. megoldás jelöléseit, és írjuk fel az \(\displaystyle AB\) szakasz \(\displaystyle d(t)\) hosszát, pontosabban ennek a négyzetét az idő függvényében! Mérjük az időt attól a pillanattól, amikor \(\displaystyle AB\) éppen a legrövidebb, azaz úgy, hogy \(\displaystyle d(0)=d_0\) legyen!

\(\displaystyle d(t)^2=(d_1-v_1t)^2+(d_2+v_2t)^2=(d_1^2+d_2^2)+2(d_2v_2-d_1v_1)t+( v_1^2+v_2^2)t^2.\)

Ennek a \(\displaystyle t\)-ben kvadratikus kifejezésnek akkor van \(\displaystyle t=0\)-ban minimuma, ha a lineáris tag együtthatója eltűnik, azaz

\(\displaystyle \frac{d_2}{d_1}=\frac{v_1}{v_2}.\)

Ez a

\(\displaystyle d_0^2=d_1^2+d_2^2\)

egyenlettel együtt természetesen ugyanazt adja \(\displaystyle d_1\)-re és \(\displaystyle d_2\)-re, mint az előző megoldás. Ebben a gondolatmenetben az, hogy melyik motoros halad át előbb a kereszteződésen, a lineáris tag előjelében jelenik meg: ha a \(\displaystyle v_1\) sebességű az, akkor a távolság négyzetének az egyenlete

\(\displaystyle d(t)^2=(d_1+v_1t)^2+(d_2-v_2t)^2=(d_1^2+d_2^2)-2(d_2v_2-d_1v_1)t+( v_1^2+v_2^2)t^2.\)

Ez az előjel azonban a megoldás szempontjából érdektelen, hisz az pont arra épül, hogy az adott tag nulla.

III. megoldás. Jelöljük az első motoros kiindulási helyét \(\displaystyle A\)-val, a másodikét \(\displaystyle B\)-vel, az utak kereszteződését pedig \(\displaystyle O\)-val. Az irányokra történő hivatkozások megkönnyítése érdekében tételezzük fel, hogy az első motoros \(\displaystyle v_1\) sebességgel halad kelet felé, a második pedig \(\displaystyle v_2\) sebességgel észak felé. Ezek a sebességek a talajhoz viszonyítottak, tehát az ,,álló'' \(\displaystyle \cal{K}\) koordináta-rendszerben értendők (lásd a 2. ábra felső felét).

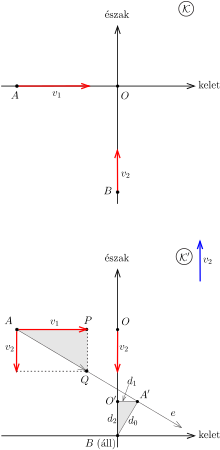
2. ábra

Üljünk most bele a \(\displaystyle \cal{K}\)-hoz képest \(\displaystyle v_2\) sebességgel észak felé mozgó \(\displaystyle \cal{K}'\) koordináta-rendszerbe, és írjuk le onnan nézve a motorosok mozgását. Ebben a rendszerben a második motoros áll, az első pedig \(\displaystyle v_1\) sebességgel halad kelet felé, miközben \(\displaystyle v_2\) nagyságú, dél felé irányuló sebességgel is rendelkezik (lásd a 2. ábra alsó felét). Az első motoros tehát \(\displaystyle \sqrt{v_1^2+v_2^2}\) nagyságú sebességgel nagyjából délkelet felé halad az \(\displaystyle e\) jelű egyenes mentén. Az utak kereszteződési pontja ugyancsak mozogni fog \(\displaystyle \cal{K}'\)-ben, nevezetesen \(\displaystyle v_2\) sebességgel halad dél felé.

A két motoros abban az \(\displaystyle A'\) pontban kerül egymáshoz legközelebb, amelyet a \(\displaystyle B\)-ből \(\displaystyle e\)-re bocsátott merőleges egyenes jelöl ki. A 2. ábra alsó felén két (szürkén jelölt) derékszögű háromszöget látunk. Ezek megfelelő oldalainak arányából leolvashatjuk, hogy

\(\displaystyle \frac{d_1}{d_0}=\frac{O'A'}{A'B}=\frac{PQ}{AQ}=\frac{v_2}{\sqrt{v_1^2+v_2^2}},\)

vagyis

\(\displaystyle d_1=d_0\frac{v_2}{\sqrt{v_1^2+v_2^2}}.\)

Hasonló módon kapjuk, hogy

\(\displaystyle \frac{d_2}{d_0}=\frac{O'B}{A'B}=\frac{AP}{AQ}=\frac{v_1}{\sqrt{v_1^2+v_2^2}},\)

vagyis

\(\displaystyle d_2=d_0\frac{v_1}{\sqrt{v_1^2+v_2^2}}.\)

A fenti megfontolások során hallgatólagosan feltételeztük, hogy az \(\displaystyle A\) pontból induló első motoros érkezik hamarabb az utak kereszteződéséhez. (A 2. ábrán ezt onnan látjuk, hogy az \(\displaystyle e\) egyenes észak felől kerüli el az álló \(\displaystyle B\) pontot.) De a fordított eset is előfordulhat (lásd a 3. ábrát).

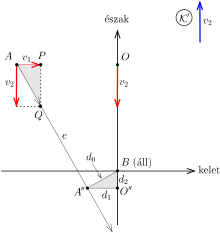
3. ábra

A megfelelő arányok összehasonlításából ebben az esetben is az előző esetével megegyező eredményt kapjuk:

\(\displaystyle d_1=d_0\frac{v_2}{\sqrt{v_1^2+v_2^2}},\qquad\textrm{illetve}\qquad d_2=d_0\frac{v_1}{\sqrt{v_1^2+v_2^2}}.\)

Statisztika:

46 dolgozat érkezett.
5 pontot kapott:	Hajdu Eszter, Kossár Benedek Balázs, Kovács Tamás, Rajtik Sándor Barnabás, Szécsi Bence, Tajta Sára, Zhao Aaron .
4 pontot kapott:	Beke Márton Csaba, Békési Máté, Bélteki Teó, Bense Tamás, Bogdán Balázs Ákos, Erdélyi Dominik, Halmosi Dávid, Hornyák Zalán Zétény, Horváth Zsombor, Kádár Luca Linda, Kovács Tamás , Mi Feiyu, Molnár Lili, Nagy Gellért Ákos, Papp Emese Petra, Patócs 420 Péter, Sándor Zsombor, Simon János Dániel, Szabó Tamás, Tasnádi Zsófia, Tóth Hanga Katalin, Zádori Gellért, Zólomy Csanád Zsolt.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	5 versenyző.

A KöMaL 2025. októberi fizika feladatai