A P. 5671. feladat (2025. október)

P. 5671. Vízszintes síkban rögzített lemezen három kicsiny lyuk van, távolságuk \(\displaystyle 3\), \(\displaystyle 4\) és \(\displaystyle 5\) egységnyi. Három vékony, hajlékony fonál egy-egy végét összecsomózzuk, a másik végüket pedig a lyukakon átfűzzük, majd a lelógó végükre (az ábrán látható módon) \(\displaystyle 2\), \(\displaystyle 3\) és \(\displaystyle 4\) egységnyi tömeget akasztunk. A fonalak és az asztal közötti súrlódás elhanyagolható.

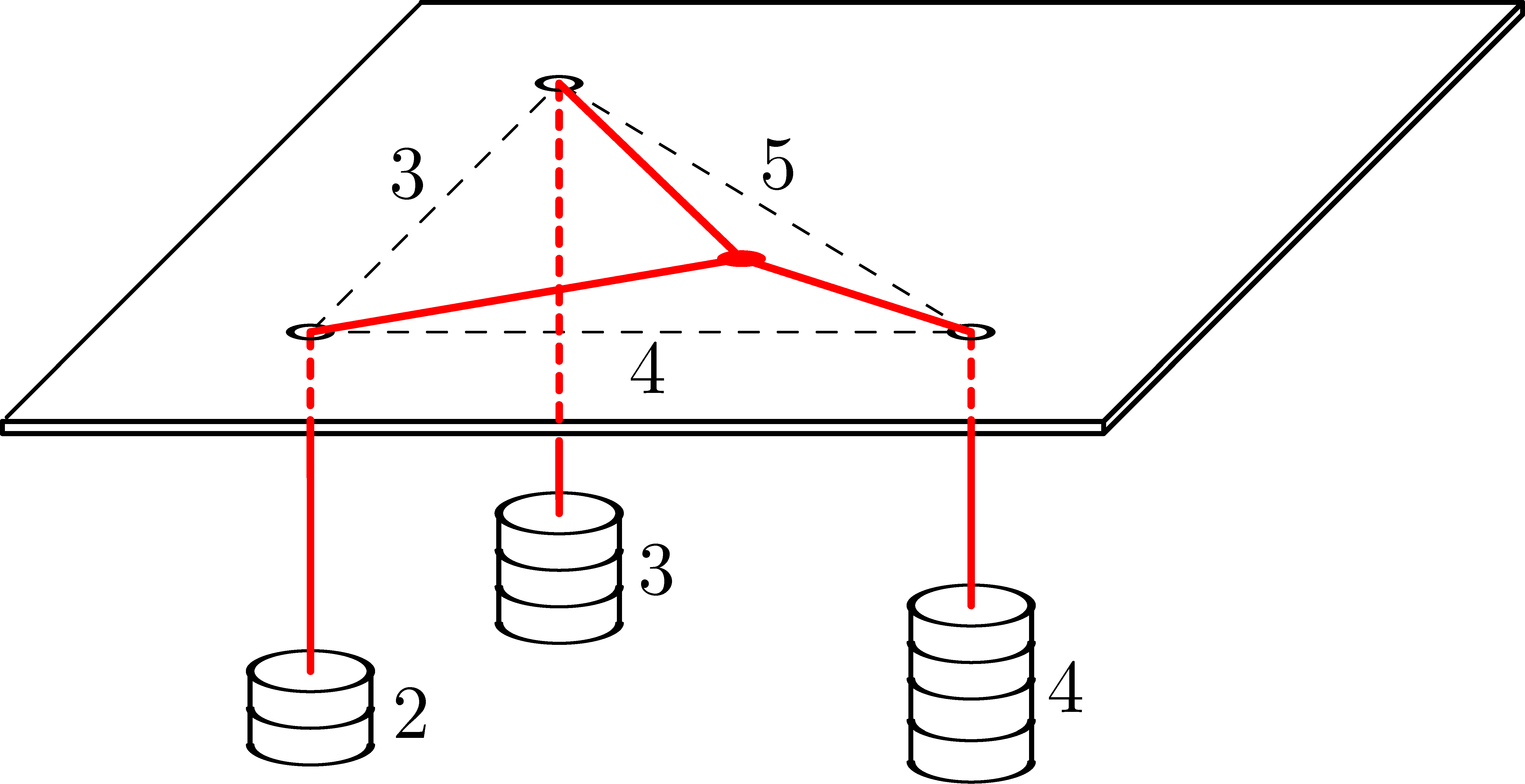
Szerkesszük meg (körzővel és vonalzóval vagy a GeoGebra program segítségével), hogy egyensúlyi helyzetben hol lesz a csomó!

Közli: Gnädig Péter, Vácduka

(5 pont)

A beküldési határidő 2025. november 17-én LEJÁRT.

Megoldás. Az 1. ábra az elrendezés felülnézeti képét mutatja. A lemezen lévő lyukak helyzetét \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) jelöli, a távolságukat (önkényesen választott egységekben) kicsiny piros körök mutatják.

A fonalakat feszítő erők az alsó végükre akasztott súlyok nagyságával arányos, tehát (ugyancsak önkényesen választható egységekben) \(\displaystyle \vert\boldsymbol{F}_A\vert=2\), \(\displaystyle \vert\boldsymbol{F}_B\vert=4\) és \(\displaystyle \vert\boldsymbol{F}_C\vert=3\). A csomó keresett egyensúlyi helyzetének, vagyis az ábrán látható \(\displaystyle P\) pontnak megszerkesztéséhez először a fonalak egymással bezárt \(\displaystyle \alpha\), \(\displaystyle \beta\) és \(\displaystyle \gamma\) szögét (vagy ezek közül legalább kettőt) fogjuk meghatározni szerkesztéssel.

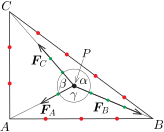
1. ábra

Egyensúlyi állapotban a csomóra ható erők eredője nulla, vagyis \(\displaystyle \boldsymbol{F}_A+\boldsymbol{F}_B+\boldsymbol{F}_C=0\). A három fonálerő vektora – azokat rendre egymás csúcsából felmérve – zárt vektorháromszöget alkot. Ezt a háromszöget az oldalak hosszának (2, 4 és 3) ismeretében könnyen megszerkeszthetjük és a kérdéses szögeket arról leolvashatjuk (2. ábra).

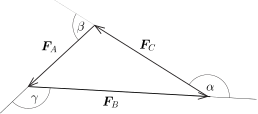
2. ábra

Az általánosított Thalész-tétel szerint azon pontok halmaza, amelyekből egy szakasz ismert nagyságú szögben látszik, két nyílt körív, amelyeknek a szakasz egy közös húrja. Például a feladatban szereplő lemez azon pontjai, amelyekből az \(\displaystyle A\) és \(\displaystyle B\) lyukak ismert nagyságú \(\displaystyle \gamma\) szögben látszanak, egy olyan köríven találhatók, amelynek \(\displaystyle AB\) az egyik húrja, és a húr végpontjainál húzható érintői hegyesszög esetén \(\displaystyle \gamma\), tompaszög esetén pedig \(\displaystyle 180^\circ-\gamma\) szöget zárnak be az \(\displaystyle AB\) húrral. Az \(\displaystyle ABC\triangle\) keresett \(\displaystyle P\) belső pontja is erre a körívre illeszkedik (3. ábra).

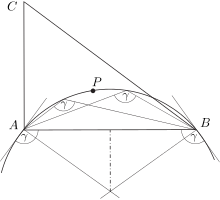
3. ábra

Az \(\displaystyle ABC\triangle\) másik két oldalára is elvégezve a látószög-körívek szerkesztését \(\displaystyle \beta\), illetve \(\displaystyle \alpha\) szögekkel, ezek (vagy ezek közül bármelyik kettő) metszéspontja megadja a csomónak a keresett egyensúlyi helyzetét (4. ábra).

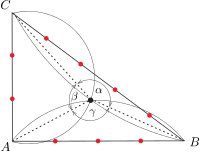
4. ábra

Megjegyzések. 1. A szerkesztés a fentebb leírtakhoz hasonló lépésekkel tetszőleges lyukelrendezés és tetszőleges súlyok mellett is elvégezhető. Az általános esetben azonban előfordulhat, hogy az erővektorok nagysága nem elégíti ki a háromszög-egyenlőtlenséget, emiatt a 2. ábrán látható háromszög nem szerkeszthető meg. Az is lehetséges, hogy az erők nagyságával arányos oldalhosszúságú háromszög megszerkeszthető ugyan, de a látószög-körívek metszéspontja az \(\displaystyle ABC\triangle\)-ön kívülre esik. Ez a külső pont nem határoz meg egyensúlyi helyzetet, vagyis a fonálerők nem alkothatnak zárt vektorháromszöget, hiszen lesz olyan egyenes (például az \(\displaystyle ABC\triangle\) valamelyik oldala), amelyre nézve az összes erő rá merőleges komponense azonos előjelű, összegük tehát nem lehet nulla. Ezekben az esetekben a csomó a háromszög egyetlen belső pontjában sem lehet egyensúlyban, hanem valamelyik lyukig mozdul el, és azon esetleg átbújva az egyik súlynak a lemezhez ütközése után alakulhat csak ki egyensúly.

2. Egy mechanikai rendszer egyensúlyi helyzetét nemcsak az erőrendszer egyensúlya, hanem a rendszer helyzeti energiájának minimuma is jellemzi. Esetünkben az energiaminimum feltétele egyenértékű azzal a geometriai feladattal, hogy keressük az \(\displaystyle ABC\triangle\) azon belső \(\displaystyle P\) pontját, amelyre a csúcspontoktól mért távolságok súlyozott összege a lehető legkisebb, vagyis

\(\displaystyle \vert\boldsymbol{F}_A\vert\cdot PA+\vert\boldsymbol{F}_B\vert\cdot PB+\vert\boldsymbol{F}_C\vert\cdot PC=\textrm{minimális}.\)

Ennek az ún. súlyozott Fermat–Torricelli-problémának többféle – tisztán geometriai, tehát fizikai fogalmakra nem hivatkozó – megoldása is megadható (lásd pl. Skljarszkij - Csencov - Jaglom: Válogatott feladatok és tételek az elemi matematika köréből II. Geometriai egyenlőtlenségek és szélsőérték feladatok, 79. probléma).

Statisztika:

A P. 5671. feladat értékelése még nem fejeződött be.

A KöMaL 2025. októberi fizika feladatai