A P. 5672. feladat (2025. október)

P. 5672. Az Egyenlítőn állva, éppen a fejünk felett halad át egy műhold, amely a Föld felszínétől \(\displaystyle 400~\mathrm{km}\)-re levő pályán kering. Legfeljebb mennyi ideig láthatjuk a műholdat?

Közli: Németh László, Fonyód

(4 pont)

A beküldési határidő 2025. november 17-én LEJÁRT.

Megoldás. Számoljuk ki először egy képzeletbeli, tengerszinten keringő műhold \(\displaystyle T_t\) keringési idejét! Ezen a pályán a centripetális gyorsulás éppen \(\displaystyle g\) nagyságú:

\(\displaystyle R\left(\frac{2\pi}{T_t}\right)^2=g,\)

ahol \(\displaystyle R=6378\,\mathrm{km}\) a Föld egyenlítői sugara. Innen

\(\displaystyle T_t=2\pi\sqrt{\frac{R}{g}}=2\pi\sqrt{\frac{6378\,\mathrm{km}}{9{,}8\,\mathrm{m/s^2}}}=84{,}48\,\mathrm{perc}.\)

(Megelégszünk két tizedes pontossággal, és nem foglalkoztunk azzal, hogy \(\displaystyle g\) értékében megjelenik néhány ezreléknyi centrifugális erő) A \(\displaystyle h=400\,\mathrm{km}\) magasan keringő műhold keringési idejét Kepler III. törvényét alkalmazva számíthatjuk:

\(\displaystyle T_m=T_t\left(\frac{R+h}{R}\right)^{1{,}5}=84{,}48\,\mathrm{perc}\left(\frac{6378\,\mathrm{km}+400\,\mathrm{km}}{6378\,\mathrm{km}}\right)^{1{,}5}=92{,}55\,\mathrm{perc}.\)

Az Egyenlítőn állva együtt forgunk a Földdel \(\displaystyle n_f=1\,\mathrm{nap}^{-1}\) fordulatszámmal. A műhold haladási irányát a feladat nem adta meg, de leghosszabb ideig akkor látjuk, ha a velünk azonos irányban, nyugatról keletre kerüli meg a Földet. A műhold földi megfigyelőhöz viszonyított fordulatszáma ekkor:

\(\displaystyle n=T_m^{-1}-n_f.\)

A földi megfigyelőhöz viszonyított keringési ideje pedig

\(\displaystyle T=\frac{1}{n}=\frac{1\,\mathrm{nap}\cdot T_m}{1\,\mathrm{nap}-T_m}=\frac{1440\,\mathrm{perc}\cdot 92{,}55\,\mathrm{perc}}{1440\,\mathrm{perc}-92{,}55\,\mathrm{perc}}=98{,}91\,\mathrm{perc}.\)

Maradjunk innentől fogva a Földdel együtt forgó koordináta-rendszerben! A műhold felbukkan a nyugati horizonton, lemegy keleten. A két helyzetben a műholdat a röppálya középpontjával (Föld középpontjával) összekötő sugarak egymással bezárt szögét jelöljük \(\displaystyle 2\alpha\)-val. Az ábra szerint:

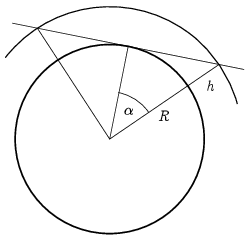
\(\displaystyle \cos\alpha=\frac{R}{R+h}=\frac{6378\,\mathrm{km}}{6778\,\mathrm{km}}=0{,}9410\quad\Rightarrow\quad\alpha=19{,}8^\circ.\)

Ezen a körív pályaszakaszon

\(\displaystyle \frac{2\alpha}{360^\circ}\cdot T=\frac{19{,}8^\circ}{180^\circ}\cdot 98{,}91\,\mathrm{perc}=10{,}9\,\mathrm{perc}\)

ideig halad a műhold, legfeljebb ennyi ideig látjuk tehát.

Statisztika:

47 dolgozat érkezett.
4 pontot kapott:	Bélteki Teó, Elekes Panni, Fuchs Vince, Kádár Luca Linda, Nagy Gellért Ákos, Sipeki Andor, Tasnádi Zsófia, Tóth Hanga Katalin, Török Tibor, Vigh István Csaba, Winhoffer Júlia.
3 pontot kapott:	Bús László Teodor, Kovács Dániel, Lakatos Levente, Magyar Levente Árpád, Mezei Marcell, Molnár Lili, Patócs 420 Péter, Sipos Dániel Sándor.
2 pontot kapott:	22 versenyző.
1 pontot kapott:	2 versenyző.

A KöMaL 2025. októberi fizika feladatai