 |
A P. 5674. feladat (2025. október) |
P. 5674. Egy hőerőgép egy \(\displaystyle C\) hőkapacitású, kezdetben \(\displaystyle T\) hőmérsékletű test és egy állandó \(\displaystyle T_0\) hőmérsékletű, nagy méretű hőtartály között üzemel.
Vizsgáljuk a következő két esetet: \(\displaystyle T=T_0+\Delta T\) és \(\displaystyle T=T_0-\Delta T\). Melyik esetben nyerhetünk több munkát?
Példatári feladat nyomán
(5 pont)
A beküldési határidő 2025. november 17-én LEJÁRT.
Megoldás. Mindkét esetben akkor maximális a munkavégzés, ha a hőerőgép minden pillanatban ideális Carnot-gépként működik. A nehézséget az okozza, hogy az egyik hőtartály hőmérséklete, és így a hatásfok is mindkét esetben folyamatosan változik, ezért csak kis elemi lépésekre írhatjuk fel az összefüggéseket, amelyeket azután összegeznünk kell.
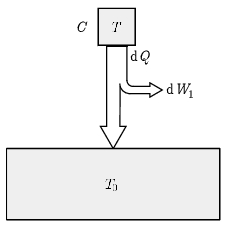
1. ábra
Az első esetben (1. ábra) a felső (melegebb) hőtartály hőmérséklete \(\displaystyle T\), amely a folyamat során végig csökken, míg az alsó (hidegebb) hőtartály hőmérséklete állandó \(\displaystyle T_0\). Ekkor a Carnot-gép ismert képlete alapján az elemi munkavégzés:
\(\displaystyle \mathrm{d}W_1=\left(1-\frac{T_0}{T}\right)\mathrm{d}Q,\)
ahol \(\displaystyle \mathrm{d}Q\) a \(\displaystyle C\) hőkapacitású, kezdetben \(\displaystyle T=T_0+\Delta T\) hőmérsékletű (majd folyamatosan hülő) test által leadott elemi hőmennyiség, amit a test hőkapacitásával és hőmérséklet-változásával is kifejezhetünk:
\(\displaystyle \mathrm{d}Q=-C\mathrm{d}T.\)
Behelyettesítve az első összefüggésbe:
\(\displaystyle \mathrm{d}W_1=C\left(1-\frac{T_0}{T}\right)(-\mathrm{d}T).\)
A teljes munkavégzést ennek összegzésével (integrálással) kaphatjuk meg (bár látni fogjuk, hogy az integrál elvégzésére az összehasonlításhoz nem lesz feltétlenül szükségünk):
\(\displaystyle W_1=\int\limits_{T_0+\Delta T}^{T_0}C\left(1-\frac{T_0}{T}\right)(-\mathrm{d}T)=\int\limits_{T_0}^{T_0+\Delta T}C\left(1-\frac{T_0}{T}\right)\mathrm{d}T=CT_0\left(\frac{\Delta T}{T_0}-\ln\left(1+\frac{\Delta T}{T_0}\right)\right).\)
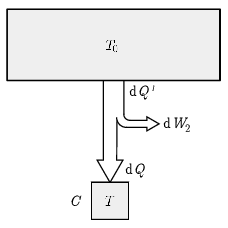
2. ábra
A második esetben (2. ábra) a felső (melegebb) hőtartály hőmérséklete állandó \(\displaystyle T_0\), míg az alsó (hidegebb) hőtartály hőmérséklete \(\displaystyle T\), amely a folyamat során végig növekszik. A Carnot-gép elemi munkavégzése:
\(\displaystyle \mathrm{d}W_2=\left(1-\frac{T}{T_0}\right)\mathrm{d}Q',\)
ahol most \(\displaystyle \mathrm{d}Q'\) az állandó \(\displaystyle T_0\) hőmérsékletű hőtartály által leadott hő. A \(\displaystyle C\) hőkapacitású, kezdetben \(\displaystyle T=T_0-\Delta T\) hőmérsékletű (majd folyamatosan melegedő) test által felvett elemi hőmennyiség:
\(\displaystyle \mathrm{d}Q=\mathrm{d}Q'-\mathrm{d}W_2=\frac{T}{T_0}\mathrm{d}Q'.\)
Ebből \(\displaystyle \mathrm{d}Q'\)-t kifejezve, és az első kifejezésbe beírva:
\(\displaystyle \mathrm{d}W_2=\left(\frac{T_0}{T}-1\right)\mathrm{d}Q,\)
majd felhasználva, hogy most
\(\displaystyle \mathrm{d}Q=C\mathrm{d}T,\)
az elemi munkavégzés kifejezése:
\(\displaystyle \mathrm{d}W_2=C\left(\frac{T_0}{T}-1\right)\mathrm{d}T.\)
A teljes munkavégzést ismét ennek összegzésével (integrálással) kaphatjuk meg (az integrál elvégzésére az összehasonlításhoz most sem lesz feltétlenül szükségünk):
\(\displaystyle W_2=\int\limits_{T_0-\Delta T}^{T_0}C\left(\frac{T_0}{T}-1\right)\mathrm{d}T=-CT_0\left(\frac{\Delta T}{T_0}+\ln\left(1-\frac{\Delta T}{T_0}\right)\right).\)
Ezután el kell döntenünk, hogy melyik munkavégzés nagyobb: erre két módszert mutatunk.
I. Az integrál elvégzése nélkül. Mindkét esetben egy \(\displaystyle \Delta T\) hosszúságú intervallumon végezzük az integrálást: az egyik esetben \(\displaystyle T_0\)-ról indulva \(\displaystyle T_0+\Delta T\)-ig, a másik esetben \(\displaystyle T_0-\Delta T\)-ről indulva \(\displaystyle T_0\)-ig (3. ábra). Hasonlítsuk össze a két integrandust! Az első esetben
\(\displaystyle T_0\leq T\leq T_0+\Delta T\quad\Rightarrow\quad T=T_0+\delta T,\)
míg a második esetben
\(\displaystyle T_0-\Delta T\leq T\leq T_0\quad\Rightarrow\quad T=T_0-\delta T,\)
ahol \(\displaystyle 0\leq\delta T\leq\Delta T\). Ez alapján viszont a két integrandus összehasonlítása (a \(\displaystyle C\) konstanst mindkét esetben elhagyva):
\(\displaystyle 1-\frac{T_0}{T}=1-\frac{T_0}{T_0+\delta T}=\frac{\delta T}{T_0+\delta T}\leq\frac{\delta T}{T_0-\delta T}=\frac{T_0}{T_0-\delta T}-1=\frac{T_0}{T}-1,\)
azaz a második esetben az integrandus mindig nagyobb (az intervallum szélén pedig egyenlő). Tehát a második esetben nyerhető több munka.
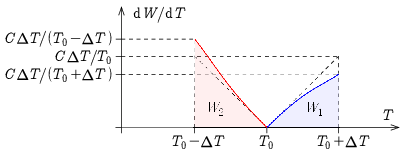
3. ábra
II. Az integrálok összehasonlítása sorfejtéssel. A két munkavégzést is összehasonlíthatjuk, ehhez a fenti integrálásokkal kapott kifejezésekben a logaritmus függvényt sorba kell fejtenünk. Táblázatokban megtalálható:
\(\displaystyle \ln x=\sum\limits_{n=1}^\infty\frac{(-1)^{n-1}}{n}(x-1)^n.\)
A sorbafejtést mindkét esetben az első három tagig elvégezve:
$$\begin{gather*} \frac{W_1}{CT_0}=\frac{\Delta T}{T_0}-\ln\left(1+\frac{\Delta T}{T_0}\right)=\frac{\Delta T}{T_0}-\frac{\Delta T}{T_0}+\frac{1}{2}\left(\frac{\Delta T}{T_0}\right)^2-\frac{1}{3}\left(\frac{\Delta T}{T_0}\right)^3=\frac{1}{2}\left(\frac{\Delta T}{T_0}\right)^2-\frac{1}{3}\left(\frac{\Delta T}{T_0}\right)^3\\ \frac{W_2}{CT_0}=-\frac{\Delta T}{T_0}-\ln\left(1-\frac{\Delta T}{T_0}\right)=-\frac{\Delta T}{T_0}+\frac{\Delta T}{T_0}+\frac{1}{2}\left(\frac{\Delta T}{T_0}\right)^2+\frac{1}{3}\left(\frac{\Delta T}{T_0}\right)^3=\frac{1}{2}\left(\frac{\Delta T}{T_0}\right)^2+\frac{1}{3}\left(\frac{\Delta T}{T_0}\right)^3. \end{gather*}$$Tehát \(\displaystyle W_2>W_1\), azaz a második esetben nyerhető több munka.
Megjegyzés. Csak az első három tagot írtuk fel a sorfejtésben, mert \(\displaystyle \Delta T<T_0\) miatt a további tagok egyre kisebbek. De az is belátható, hogy a páros tagok mindvégig megegyeznek, a páratlanok pedig a harmadik taghoz hasonlóan az első esetben negatívak, a másodikban pozitívak, így a további tagok a két kifejezés közti különbséget tovább növelik.
Statisztika:
A P. 5674. feladat értékelése még nem fejeződött be.
A KöMaL 2025. októberi fizika feladatai