 |
A P. 5675. feladat (2025. október) |
P. 5675. \(\displaystyle 30~\mathrm{cm}\) oldalhosszúságú, szabályos háromszög csúcsaiban \(\displaystyle 400~\mathrm{nC}\) nagyságú, pontszerű töltések vannak. A szomszédos töltéseket szigetelőfonalak kötik össze.
a) Mekkora erő feszíti a fonalakat?
b) Mekkora erő feszíti a fonalakat akkor, ha a háromszög súlypontjába egy \(\displaystyle 200~\mathrm{nC}\) nagyságú töltést helyezünk el?
Közli: Veres Dénes, Szolnok
(4 pont)
A beküldési határidő 2025. november 17-én LEJÁRT.
Megoldás. a) Minden \(\displaystyle q=400\,\mathrm{nC}\) nagyságú töltésre két, egyforma nagyságú \(\displaystyle K\) fonálerő és két, egyforma nagyságú \(\displaystyle F_\mathrm{C}\) Coulomb-erő hat (1. ábra).
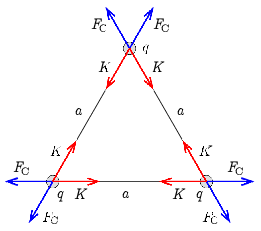
1. ábra
Mivel a fonálerők és az elektrosztatikus erők is a háromszög oldalaival párhuzamosak, csak úgy lehet egyensúly, ha \(\displaystyle K=F_\mathrm{C}\). Így a fonálerők nagysága (\(\displaystyle a=0{,}3\,\mathrm{m}\) és \(\displaystyle k=9\cdot 10^9\,\mathrm{Nm^2/C^2}\) felhasználásával):
\(\displaystyle K=F_\mathrm{C}=\frac{kq^2}{a^2}=0{,}016\,\mathrm{N}.\)
b) Ebben az esetben a háromszög csúcsaiban elhelyezkedő töltésekre a középpontba elhelyezett \(\displaystyle Q=200\,\mathrm{nC}\) nagyságú töltés Coulomb-ereje is hat (2. ábra). A fonálerőknek az eddigieken kívül ezt a taszító erőt is meg kell tartaniuk.
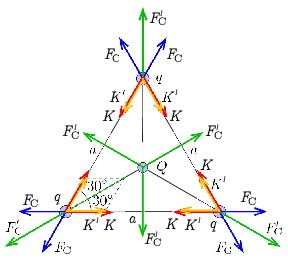
2. ábra
Az ábra alapján az új fonálerő:
\(\displaystyle K_2=K+K'=K+\frac{1}{2\cos 30^\circ}\,F_\mathrm{C}'=K+\frac{1}{\sqrt{3}}\frac{kqQ}{\left(a/\sqrt{3}\right)^2}=K+\frac{\sqrt{3}kqQ}{a^2}=0{,}016\,\mathrm{N}+0{,}014\,\mathrm{N}=0{,}030\,\mathrm{N}.\)
Statisztika:
43 dolgozat érkezett. 4 pontot kapott: Bense Tamás, Blaskovics Ádám, Bogdán Balázs Ákos, Bús László Teodor, Fuchs Vince, Gombos Barna, Kossár Benedek Balázs, Misik Balázs, Murányi Nimród Máté, Nagy Gellért Ákos, Papp Emese Petra, Szécsi Bence, Tajta Sára, Tasnádi Zsófia, Török Tibor, Vincze Anna, Zádori Gellért, Zhao Aaron . 3 pontot kapott: Bélteki Teó, Ferencz Kevin, Gilyán Zsombor, Halmosi Dávid, Illés Dóra, Molnár Lili, Patócs 420 Péter, Vértesi Janka, Wolf Erik. 2 pontot kapott: 10 versenyző. 1 pontot kapott: 2 versenyző.
A KöMaL 2025. októberi fizika feladatai

