 |
A P. 5676. feladat (2025. október) |
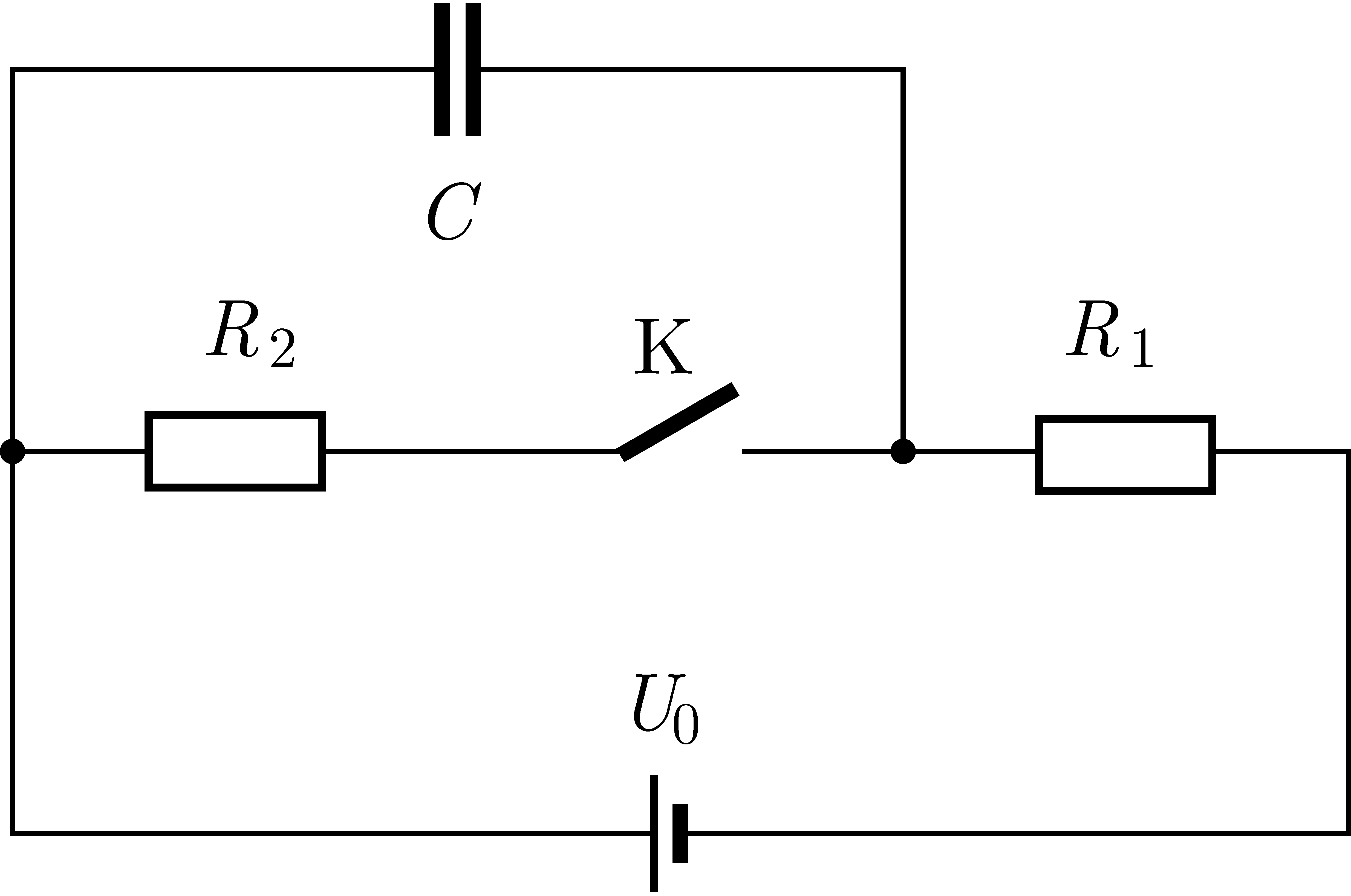
P. 5676. Az ábrán látható kapcsolási rajz szerint összeállított áramkörben szereplő feszültségforrás elektromotoros ereje \(\displaystyle 20~\mathrm{V}\), az ellenállások \(\displaystyle R_1=50~\Omega\), illetve \(\displaystyle R_2=150~\Omega\) nagyságúak, a kondenzátor \(\displaystyle 20~\mu\mathrm{F}\) kapacitású. Kezdetben a K kapcsoló zárva van.
a) Mekkora a kondenzátor töltése a kapcsoló zárt állása esetén?
b) A kapcsoló nyitását követően kialakuló állandósult állapot eléréséig mennyivel változik meg a kondenzátor energiája, és mennyi hő fejlődik az \(\displaystyle R_1\) ellenálláson?
A feszültségforrás belső ellenállása elhanyagolható.
Tornyai Sándor fizikaverseny, Hódmezővásárhely
(5 pont)
A beküldési határidő 2025. november 17-én LEJÁRT.
Megoldás. a) A kapcsoló zárt állása esetén az ellenállásokon az ellenállások arányában oszlik meg a feszültség, a kondenzátor feszültsége pedig a vele párhuzamosan kötött \(\displaystyle R_2\) ellenállás feszültségével lesz egyenlő. Így a kondenzátor feszültsége
\(\displaystyle U_\mathrm{C}=U_2=\frac{R_2}{R_1+R_2}U_0=15\,\mathrm{V},\)
a kondenzátor keresett töltése pedig:
\(\displaystyle Q=CU_\mathrm{C}=300\,\mu\mathrm{C}.\)
b) A kapcsoló kinyitása után egy tranziens folyamat kezdődik, majd a tranziens lezajlása után már nem fog sehol áram folyni az áramkörben. Ekkor a teljes telepfeszültség a kondenzátorra esik, azaz
\(\displaystyle U_\mathrm{C}'=U_0=20\,\mathrm{V},\)
és így a kondenzátor új töltése:
\(\displaystyle Q'=CU_\mathrm{C}'=400\,\mu\mathrm{C}.\)
A kondenzátor energiájának megváltozása:
\(\displaystyle \Delta E=E'-E=\frac{1}{2}CU_\mathrm{C}'^2-\frac{1}{2}CU_\mathrm{C}^2=1{,}75\,\mathrm{mJ}.\)
Eközben a telepen is áthalad \(\displaystyle \Delta Q=Q'-Q=100\,\mu\mathrm{C}\) töltés, így a telep munkavégzése:
\(\displaystyle W=\Delta QU_0=2\,\mathrm{mJ}.\)
Az \(\displaystyle R_1\) ellenálláson felszabaduló Joule-hő a telep munkavégzésének és a kondenzátor energianövekményének a különbsége:
\(\displaystyle W_1=W-\Delta E=0{,}25\,\mathrm{mJ}.\)
Megjegyzés. A feladat megoldásához nem szükséges, de leírhatjuk a tranziens folyamatot is. A huroktörvény alapján:
\(\displaystyle U_0=R_1I(t)+U_\mathrm{C}(t),\)
ahol
\(\displaystyle I=C\frac{\mathrm{d}U_\mathrm{C}(t)}{\mathrm{d}t}=C\frac{\mathrm{d}(U_\mathrm{C}(t)-U_0)}{\mathrm{d}t}.\)
Ezt behelyettesítve:
\(\displaystyle \frac{\mathrm{d}(U_\mathrm{C}(t)-U_0)}{\mathrm{d}t}=-\frac{1}{R_1C}(U_\mathrm{C}(t)-U_0),\)
amely egy ugyanolyan differenciálegyenlet az \(\displaystyle U_\mathrm{C}(t)-U_0\) mennyiségre, mint a jól ismert bomlási törvény. Ez alapján a megoldása:
\(\displaystyle U_\mathrm{C}(t)-U_0=(U_\mathrm{C}(0)-U_0)\,\mathrm{e}^{-\frac{t}{\tau}},\)
ahol \(\displaystyle \tau=R_1C\) az időállandó. Az áram időfüggése ez alapján:
\(\displaystyle I(t)=C\frac{\mathrm{d}U_\mathrm{C}(t)}{\mathrm{d}t}=\frac{U_0-U_\mathrm{C}(0)}{R_1}\,\mathrm{e}^{-\frac{t}{\tau}},\)
a teljes felszabaduló Joule-hőt pedig ennek integrálásával kaphatjuk meg:
\(\displaystyle W_1=\int\limits_0^\infty R_1I(t)^2\,\mathrm{d}t=\frac{(U_0-U_\mathrm{C}(0))^2}{R_1}\int\limits_0^\infty \mathrm{e}^{-\frac{2t}{\tau}}\,\mathrm{d}t=\frac{C}{2}(U_0-U_\mathrm{C}(0))^2=0{,}25\,\mathrm{mJ},\)
az előző megoldással összhangban.
Statisztika:
A P. 5676. feladat értékelése még nem fejeződött be.
A KöMaL 2025. októberi fizika feladatai