 |
A P. 5678. feladat (2025. október) |
P. 5678. Egy \(\displaystyle D\) rugóállandójú rugó egyik végét egy lift mennyezetéhez rögzítjük, másik végére pedig egy \(\displaystyle m\) tömegű testet akasztunk. Kezdetben a test egyensúlyban van. Egyszer csak a lift állandó \(\displaystyle a\) gyorsulással elindul felfelé, majd \(\displaystyle \tau\) idő után a gyorsulás megszűnik és a felvonó állandó sebességgel halad tovább. Mekkora amplitúdójú mozgást végez ezután a test?
Közli: Vigh Máté, Herceghalom
(6 pont)
A beküldési határidő 2025. november 17-én LEJÁRT.
I. megoldás. A felfüggesztett test mozgását végig a lifthez rögzített vonatkoztatási rendszerben írjuk le. Amíg a rendszer nyugalomban van, a rugó \(\displaystyle x_0\) megnyúlása akkora, hogy a rugóerő pont kiegyenlíti a rugón függő test \(\displaystyle mg\) súlyát, azaz \(\displaystyle x_0=\tfrac{mg}{D}\). Amikor a lift egyenletesen gyorsulva elindul fölfelé, a hozzá rögzített koordináta-rendszerben megjelenik egy \(\displaystyle ma\) nagyságú lefelé mutató tehetetlenségi erő. Ez hatásában ugyanolyan, mintha a nehézségi gyorsulás \(\displaystyle a\)-val megnövekedne, tehát a gyorsulás alatt \(\displaystyle g_\mathrm{eff}=g+a\). Ennek megfelelően az \(\displaystyle m\) tömeg ,,egyensúlyi'' helyzete (az a helyzet, ahol a rugóerő pont kompenzálná az effektív súlyerőt) \(\displaystyle \Delta x=\tfrac{ma}{D}\) értékkel lejjebb kerül, és amíg a lift gyorsul, a test e körül fog \(\displaystyle \omega=\sqrt{\tfrac{D}{m}}\) körfrekvenciával rezgőmozgást végezni. A rezgés kezdetekor a testnek az egyensúlyi helyzettől mért kitérése éppen \(\displaystyle \Delta x\), sebessége pedig nulla, ezért az \(\displaystyle x\) kitérés és a lifthez viszonyított \(\displaystyle v\) sebesség a \(\displaystyle t\) idő függvényében
\(\displaystyle x(t)=\Delta x\cos\omega t\qquad\textrm{és}\qquad v(t)=-\omega\Delta x\sin\omega t.\)
Amint megszűnik a lift gyorsulása, az egyensúlyi helyzet visszakerül az \(\displaystyle x_0\)-lal jellemzett pozícióba és a test rezgése változatlan körfrekvenciával e körül a pont körül folytatódik. Innentől a mozgás jellemzőit az
\(\displaystyle x^\prime(t)=A\cos(\omega(t-\tau)+\varphi)\qquad\textrm{és}\qquad v^\prime(t)=-\omega A\sin(\omega(t-\tau)+\varphi)\)
egyenletek adják meg azzal, hogy az \(\displaystyle x^\prime\) távolságot az új (egyben a gyorsulás előtti) egyensúlyi pozíciótól kell mérni. Figyelembe véve, hogy ez a pont a liftben \(\displaystyle \Delta x\)-szel magasabban van mint az, ahonnan \(\displaystyle x\)-et mérjük, a \(\displaystyle t=\tau\) időpontban
\(\displaystyle x^\prime(\tau)+\Delta x=x(\tau)\qquad\textrm{és}\qquad v^\prime(\tau)=v(\tau),\)
azaz
\(\displaystyle A\cos\varphi=\Delta x\left(\cos\omega\tau-1\right)\qquad\textrm{és}\qquad A\sin\varphi=\Delta x\sin\omega\tau.\)
E két utóbbi egyenletet négyzetre emelve és összeadva \(\displaystyle \varphi\)-t kiküszöböljük az egyenletből:
\(\displaystyle A^2=2(1-\cos\omega\tau)(\Delta x)^2,\)
végül kihasználjuk, hogy \(\displaystyle \Delta x=\tfrac{ma}{D}\) és \(\displaystyle \omega=\sqrt{\tfrac{D}{m}}\), így
\(\displaystyle A=\sqrt{2\left(1-\cos\sqrt{\frac{D}{m}}\tau\right)}\,\frac{ma}{D}.\)
Megjegyzés. A kialakuló amplitúdó \(\displaystyle \tau\) értékétől függően 0 és \(\displaystyle 2\tfrac{ma}{D}\) között változhat. Maximális amplitúdó akkor lesz, ha \(\displaystyle \cos\sqrt{\tfrac{D}{m}}\tau=-1\), azaz ha \(\displaystyle \tau=(2n+1)\pi\sqrt{\tfrac{m}{D}}\), \(\displaystyle n\in \mathbb{N}\). A test egyáltalán nem fog rezegni, ha \(\displaystyle \cos\sqrt{\tfrac{D}{m}}\tau=1\), azaz ha \(\displaystyle \tau=2n\pi\sqrt{\tfrac{m}{D}}\), \(\displaystyle n\in \mathbb{N}\).
II. megoldás. A feladatot megoldhatjuk inerciarendszerből (pl. a talajhoz rögzített ,,álló'' koordináta-rendszerből) nézve is. Ebben a rendszerben a Newton-egyenletek az eredeti alakjukban érvényesek, nincs szükség ,,tehetetlenségi erők'' bevezetésére.
A megoldás menetét – a jobb áttekinthetőség kedvéért – több lépésre bontjuk.
1. lépés: A lift megindulása előtti állapot vizsgálata.
Legyen a rugó nyújtatlan hossza \(\displaystyle \ell_0\), az \(\displaystyle m\) tömegű test ráakasztása után pedig \(\displaystyle \ell=\ell_0+x_0\). Egyensúlyi helyzetben a testre ható eredő erő
| \(\displaystyle (1)\) | \(\displaystyle F=Dx_0-mg=0,\qquad\textrm{vagyis}\qquad x_0=\frac{mg}{D}.\) |
Válasszunk egy olyan koordináta-rendszert, amelynek \(\displaystyle x\) tengelye függőlegesen felfelé mutat (tehát minden vektort ebben az irányban tekintünk pozitívnak), és a origója a test nyugalmi helyzeténél van, amikor a lift még áll.
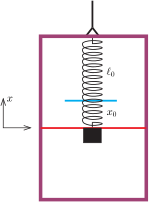
1. ábra
Ezt a helyet a lift oldalán is megjelöljük egy piros vonallal, hogy a helyét akkor is jól láthassuk, amikor a lift már mozgásba jött (1. ábra).
2. lépés: Az \(\displaystyle m\) tömegű test mozgásegyenletének felírása a lift gyorsuló mozgásakor.
A lift \(\displaystyle t=0\) pillanatban elkezd függőlegesen felfelé \(\displaystyle a\) gyorsulással mozogni, tehát \(\displaystyle t\) idő alatt \(\displaystyle \frac{a}{2}t^2\) utat tesz meg. Ezalatt az \(\displaystyle m\) tömegű test elmozdulása a korábban választott inerciarendszerben legyen \(\displaystyle x(t)\) (2. ábra). Első feladatunk ezen \(\displaystyle x(t)\) függvény meghatározása.
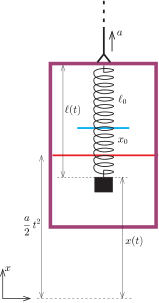
2. ábra
A lift teteje \(\displaystyle t\) idő alatt \(\displaystyle \frac{a}{2}t^2\)-tel került magasabbra, így a rugó hossza
\(\displaystyle \ell(t)=\frac{a}{2}t^2-x(t)+\ell_0+x_0,\)
a megnyúlása pedig
\(\displaystyle \varDelta\ell=\ell(t)-\ell_0=\frac{a}{2}t^2-x(t)+x_0\)
lesz. A testre ható eredő erő
\(\displaystyle F(t)=D\,\varDelta\ell-mg=D\frac{a}{2}t^2-D\,x(t)+(Dx_0-mg).\)
A zárójelben álló kifejezés (1) miatt nulla, így
| \(\displaystyle (2)\) | \(\displaystyle F(t)=D\frac{a}{2}t^2-D\,x(t).\) |
Newton mozgástörvénye szerint az \(\displaystyle F\) erő az \(\displaystyle m\) tömeg és a test gyorsulásának szorzatával egyenlő. A gyorsulásra nem a megszokott jelölést használjuk, mert az ,,\(\displaystyle a\)'' betű már ,,foglalt'', az a lift gyorsulását jelöli. Ehelyett az elméleti fizika szakkönyvekben szokásos módon egy fizikai mennyiség változási sebességét (az idő szerinti deriváltját) a mennyiség betűjele fölé tett ponttal, a sebesség változási ütemét (a gyorsulást, vagyis az idő szerinti második deriváltat) a betűjel fölé tett két ponttal fogjuk jelölni. Ez a jelölés azért is praktikus, mert különbséget tud tenni különböző fizikai mennyiségek változási sebessége, illetve gyorsulása között.
A tömegpont mozgásegyenlete ezek szerint
\(\displaystyle F(t)=m\ddot{x}(t),\)
azaz a \(\displaystyle D/m=\omega^2\) jelölés bevezetésével (\(\displaystyle \omega\) az álló liftben harmonikus rezgőmozgást végző test körfrekvenciája)
| \(\displaystyle (3)\) | \(\displaystyle \ddot{x}(t)=-\omega^2\left(x(t)-\frac{a}{2}t^2\right).\) |
3. lépés: A mozgásegyenlet megoldása alkalmasan választott új függvények segítségével.
A test mozgásegyenlete egy bonyolultnak látszó ,,differenciálegyenlet'', ami azonban könnyen visszavezethető a szokásos rezgőmozgás jól ismert problémájára.
Kézenfekvő, hogy (3) jobb oldalán a zárójelben álló kifejezést tekintsük új ismeretlen függvénynek, és arra írjunk fel mozgásegyenletet. Legyen tehát
| \(\displaystyle (4)\) | \(\displaystyle y(t)\equiv x(t)-\frac{a}{2}t^2,\) |
aminek változási sebessége és gyorsulása:
| \(\displaystyle (5)\) | \(\displaystyle \dot{y}(t)=\dot{x}(t)-at,\qquad\textrm{illetve}\qquad\ddot{y}(t)=\ddot{x}(t)-a.\) |
Az új mozgásegyenlet:
| \(\displaystyle (6)\) | \(\displaystyle \ddot{y}(t)=-\omega^2\left(y(t)+\frac{a}{\omega^2}\right).\) |
Ez már majdnem egy rezgőmozgás egyenlete, amely a
| \(\displaystyle (7)\) | \(\displaystyle z(t)=y(t)+\frac{a}{\omega^2}\) |
jelöléssel már az ismert alakot ölti:
| \(\displaystyle (8)\) | \(\displaystyle \ddot{z}(t)=-\omega^2\,z(t).\) |
(Kihasználtuk, hogy az időben állandó \(\displaystyle a/\omega^2\) mennyiség változási sebessége és gyorsulása is nulla, tehát \(\displaystyle \dot{z}(t)\equiv\dot{y}(t)\) és \(\displaystyle \ddot{z}(t)\equiv\ddot{y}(t)\)).
4. lépés: A kezdőfeltételek felírása.
A mozgásegyenlet megoldását a kezdeti hely- és sebességadatok teszik egyértelművé. Kezdetben a test az origóban állt, vagyis
\(\displaystyle x(0)=0\qquad\textrm{és}\qquad\dot{x}(0)=0.\)
Felhasználva (4), (5) és (7) egyenleteket kapjuk, hogy
\(\displaystyle y(0)=0\qquad\textrm{és}\qquad\dot{y}(0)=0,\)
valamint
| \(\displaystyle (9)\) | \(\displaystyle z(0)=\frac{a}{\omega^2}\qquad\textrm{és}\qquad\dot{z}(0)=0.\) |
5. lépés: A mozgásegyenlet megoldása a kezdőfeltételek figyelembevételével.
A (8) mozgásegyenlet általános megoldása
\(\displaystyle z(t)=A_1\cos\omega t+A_2\sin\omega t,\)
ahol \(\displaystyle A_1\) és \(\displaystyle A_2\) állandók. A (9) kezdeti feltétel szerint \(\displaystyle A_1=\frac{a}{\omega^2}\) és \(\displaystyle A_2=0\), vagyis
\(\displaystyle z(t)=\frac{a}{\omega^2}\cos\omega t,\qquad\dot{z}(t)=-\frac{a}{\omega}\sin\omega t.\)
Ezt (7)-be, majd (4)-be helyettesítve megkapjuk a keresett \(\displaystyle x(t)\) függvényt és annak változási sebességét:
\(\displaystyle x(t)=\frac{a}{\omega^2}(\cos\omega t-1)+\frac{a}{2}t^2,\qquad\dot{x}(t)=-\frac{a}{\omega}\sin\omega t+at.\)
6. lépés: Az energiaviszonyok vizsgálata a lift gyorsulásának megszűntekor.
\(\displaystyle t=\tau\) pillanatban megszűnik a lift gyorsulása. Ebben a pillanatban a test a liftszekrény piros vonala (az egyensúlyi helyzet) felett
| \(\displaystyle (10)\) | \(\displaystyle y(\tau)=x(\tau)-\frac{a}{2}\tau^2=\frac{a}{\omega^2}(\cos\omega\tau-1)\leq 0\) |
magasságban (ténylegesen az alatti helyen) található. A rugó hossza ekkor
\(\displaystyle \ell(\tau)=\frac{a}{2}\tau^2-x(\tau)+\ell_0+x_0=\ell_0+\frac{a}{\omega^2}(1-\cos\omega\tau )+x_0,\)
ahol \(\displaystyle x_0=mg/D\). A rugó megnyúlása tehát ebben a pillanatban
\(\displaystyle \varDelta\ell=\frac{a}{\omega^2}(1-\cos\omega\tau)+x_0,\)
a rugalmas energia pedig
| \(\displaystyle (11)\) | \(\displaystyle E_1=\frac{1}{2}D\,(\varDelta\ell)^2=\frac{1}{2}D\left(\frac{a}{\omega^2}\right)^2\left(1-2\cos\omega\tau+\cos^2\omega\tau\right)+Dx_0\frac{a}{\omega^2}(1-\cos\omega\tau)+\frac{1}{2}D\,x_0^2.\) |
A test sebessége a talajhoz viszonyítva
\(\displaystyle \dot{x}(\tau)=a\tau-\frac{a}{\omega}\sin\omega\tau,\)
míg a lift sebessége \(\displaystyle a\tau.\)
7. lépés: ,,Beülünk'' az egyenletes sebességgel mozgó liftbe.
Térjünk most át a lifttel együtt \(\displaystyle a\tau\) sebességgel mozgó koordináta-rendszerre, ami ugyancsak inerciarendszer. Ebben a rendszerben a lift áll, a test sebessége pedig
\(\displaystyle v=\dot{x}(\tau)-a\tau=-\frac{a}{\omega}\sin\omega\tau.\)
A test mozgási energiája ebben a rendszerben \(\displaystyle t=\tau\) pillanatban
| \(\displaystyle (12)\) | \(\displaystyle E_2=\frac{1}{2}mv^2=\frac{1}{2}D\left(\frac{a}{\omega^2}\right)^2\,\sin^2\omega\tau.\) |
A test rendelkezik még valamekkora gravitációs helyzeti energiával is a lifthez képest álló vonatkoztatási rendszerben. Ha a helyzeti energiát a lift piros vonalánál (a rugó egyensúlyi helyzeténél) tekintjük nullának, akkor a (10) képletben szereplő \(\displaystyle y(\tau)\) magasságban a gravitációs helyzeti energia
| \(\displaystyle (13)\) | \(\displaystyle E_3=mgy(\tau)=Dx_0\frac{a}{\omega^2}(\cos\omega\tau-1).\) |
8. (utolsó) lépés: A test összenergiájának és a rezgésének amplitúdójának kiszámítása. A lift koordináta-rendszerében a rezgő test összenergiája (11), (12) és (13) felhasználásával
\(\displaystyle E_\text{összes}=E_1+E_2+E_3=D\left(\frac{a}{\omega^2}\right)^2(1-\cos\omega\tau)+\frac{1}{2}D\,x_0^2.\)
Ez az összenergia a továbbiakban állandó marad, és a nagysága kifejezhető a rezgés \(\displaystyle A\) amplitúdójával is. Az egyensúlyi helyzeten való áthaladáskor a test helyzeti energiája nulla, a mozgási energiája \(\displaystyle \tfrac{1}{2}m(A\omega)^2\), a rugó rugalmas energiája pedig \(\displaystyle \tfrac{1}{2}D\,x_0^2\). Felírhatjuk tehát, hogy
\(\displaystyle D\left(\frac{a}{\omega^2}\right)^2(1-\cos\omega\tau)+\frac{1}{2}D\,x_0^2=\frac{1}{2}mA^2\omega^2+\frac{1}{2}D\,x_0^2\)
ahonnan a keresett rezgési amplitúdó:
\(\displaystyle A=\frac{a}{\omega^2}\sqrt{2(1-cos\omega\tau)}\qquad\left(\omega=\sqrt{D/m}\right).\)
III. megoldás. A feladatot a szuperpozíció módszerével is meg lehet oldani. Ez a módszer a mechanikában azért működik, mert egy tömegpont \(\displaystyle x(t)\) elmozdulásfüggvénye, illetve az \(\displaystyle \ddot{x}(t)\) gyorsulásfüggvénye, valamint a testre ható (időben akár változó) \(\displaystyle F(t)\) erő között lineáris kapcsolat áll fenn. Ez annyit jelent, hogy ha az \(\displaystyle x_1(t)\) elmozdulásfüggvénynek \(\displaystyle F_1(t)\) erőfüggvény felel meg, \(\displaystyle x_2(t)\)-nek pedig \(\displaystyle F_2(t)\), akkor a \(\displaystyle c_1\,x_1(t)+c_2\,x_2(t)\) elmozduláshoz tartozó erőfüggvény \(\displaystyle c_1\,F_1(t)+c_2\,F_2(t)\), ahol \(\displaystyle c_1\) és \(\displaystyle c_2\) tetszőleges állandó számok. (Ez a tulajdonság abból következik, hogy a deriválás lineáris művelet, Newton II. törvénye pedig lineáris egyenlet.)
Megjegyzés. Valamilyen ismert erőfüggvény csak a kezdőfeltételekkel együtt határozza meg egyértelműen az elmozdulásfüggvényt. Különböző megoldások súlyozott összegének képzésekor a kezdeti hely- és sebességadatok is szuperponálódnak. Ezzel azonban nem kell törődjünk, ha a kezdeti feltétel pl. az, hogy a test kezdetben az origóban áll.
Írjuk le az \(\displaystyle m\) tömegű test mozgását a lift koordináta-rendszerében. Amennyiben a test elmozdulását a rugó nyugalmi helyzetétől mérjük (ahol a rugóerő egyensúlyt tart a nehézségi erővel), akkor az \(\displaystyle mg\) nehézségi erőt a továbbiakban figyelmen kívül hagyhatjuk. A test mozgásegyenlete általánosan:
\(\displaystyle m\ddot{x}=-D\,x(t)+F(t),\)
ahol \(\displaystyle F(t)\) a testre még a rugóerőn kívül ható tetszőleges erő, \(\displaystyle \ddot{x}\) pedig a gyorsulást jelöli. Esetünkben
| \(\displaystyle (14)\) | \(\displaystyle F(t)=\begin{cases}ma,&\textrm{ha }0<t<\tau\\0,&\textrm{egyébként}.\end{cases}\) |
(A koordinátatengelyt lefelé irányítjuk, ezért a felfelé, állandó \(\displaystyle a\) gyorsulással mozgó liftben fellépő tehetetlenségi erő \(\displaystyle +ma\).) Bevezetve az \(\displaystyle \omega=\sqrt{D/m}\) jelölést a mozgásegyenlet így írható:
\(\displaystyle \ddot{x}+\omega^2x(t)=\frac{1}{m}F(t).\)
Tekintsük először azt az egyszerűbb esetet, amikor \(\displaystyle F(t)\) egy nagyon rövid \(\displaystyle \varDelta t\) ideig tartó, \(\displaystyle ma\) nagyságú erőlökés a \(\displaystyle t=0\) pillanatban. Ez az erőlökés a kezdetben álló testet hirtelen \(\displaystyle F\varDelta t/m=a\varDelta t\) sebességre gyorsítja fel (3. ábra), és az a továbbiakban \(\displaystyle \omega\) körfrekvenciájú, szinuszos rezgésbe kezd:
\(\displaystyle x(t;0)=\begin{cases}0,&\textrm{ha }t\le0\\ \frac{a\varDelta t}{\omega}\,\sin\omega t,&\textrm{ha }t>0.\end{cases}\)
(Az \(\displaystyle x(t;0)\) képletében a 0 szám azt jelöli, hogy az erőlökés \(\displaystyle t=0\) pillanatot követően történt.)
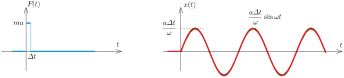
3. ábra
Amennyiben egy ugyanekkora erőlökés éri a testet valamely \(\displaystyle t'\) időpillanatot követő \(\displaystyle \varDelta t\) intervallumban (\(\displaystyle 0<t'<\tau\)), akkor ennek hatására kialakuló mozgás (lásd a 4. ábrát):
\(\displaystyle x(t;t')=\begin{cases}0,&\textrm{ha }t\le t'\\ \frac{a\varDelta t}{\omega}\,\sin\omega(t-t'),&\textrm{ha }t>t'.\end{cases}\)
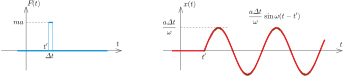
4. ábra
Mivel a (14) képletben szereplő \(\displaystyle F(t)\) függvény összetehető (szuperponálható) sok rövid erőlökésből, a ténylegesen kialakuló mozgás is előállítható az egyes erőlökésekhez tartozó elmozdulásfüggvények összegeként:
\(\displaystyle x(t)=\sum_{t'=0}^{\tau}x(t;t')=\frac{a}{\omega}\sum_{t'=0}^{\tau}\sin\omega(t-t')\,\varDelta t',\qquad\textrm{ha}\quad t>\tau.\)
Érdemes áttérni a \(\displaystyle t'\) változóról a
\(\displaystyle \varphi\equiv\omega(t-t')\)
új változóra. Mivel az erőlökések ,,szélességének'' megegyező \(\displaystyle \varDelta t'\) időintervallumnak \(\displaystyle \varDelta\varphi=\omega\,\varDelta t'\) felel meg, az összegzés határait pedig a \(\displaystyle \omega(t-\tau)<\varphi<\omega t\), a keresett megoldás így írható:
| \(\displaystyle (15)\) | \(\displaystyle x(t)=\frac{a}{\omega^2}\sum_{\varphi=\omega(t-\tau)}^{\omega t}\sin\varphi\,\varDelta \varphi.\) |
A (15) egyenlet jobb oldalán szereplő, \(\displaystyle W=\sum_{\varphi_1}^{\varphi_2}\sin\varphi\,\varDelta \varphi\) alakú összeg akár az integrálszámítás összefüggéseivel, akár fizikai megfontolásokkal is kiszámítható. Az erőlökések időtartamának fokozatos csökkentésével
| \(\displaystyle (16)\) | \(\displaystyle W\approx \int\limits_{\varphi_1}^{\varphi_2}\sin\varphi\mathrm{d}\varphi=-\cos\varphi\Big\vert_{\varphi_1}^{\varphi_2}=\cos\varphi_1-\cos\varphi_2.\) |
Megjegyzés. Ugyanezt az összefüggést megkaphatjuk úgy is, hogy egy \(\displaystyle \ell\) hosszúságú, \(\displaystyle m\) tömegű fonálinga \(\displaystyle \varphi_1\) szögtől \(\displaystyle \varphi_2\) szögig történő lassú kitérítésnél végzett munkát, illetve a helyzeti energia változását hasonlítjuk össze (5. ábra)
\(\displaystyle \sum_{\varphi_1}^{\varphi_2}(mg\sin\varphi)\,(\ell\varDelta\varphi)=mg\ell(\cos\varphi_1-\cos\varphi_2),\)
ami nyilván egyenértékű (16)-tal.
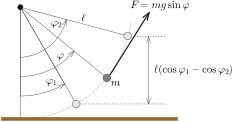
5. ábra
A fentiek szerint a (15)-ben szereplő elmozdulásfüggvény \(\displaystyle t>\tau\) időpontokban
\(\displaystyle x(t)=\frac{a}{\omega^2}\cos\left(\omega t-\omega\tau\right)-\frac{a}{\omega^2}\cos(\omega t),\)
ami – trigonometrikus átalakítás után – ilyen alakban is felírható:
| \(\displaystyle (17)\) | \(\displaystyle x(t)=A_1\cos\omega t+A_2\sin\omega t,\) |
ahol
| \(\displaystyle (18)\) | \(\displaystyle A_1=\frac{a}{\omega^2}\left(\cos\omega\tau-1\right)\qquad\textrm{és}\qquad A_2=\frac{a}{\omega^2}\sin\omega\tau.\) |
Két (különböző fázisú) harmonikus rezgés összege is harmonikus rezgőmozgás. Kérdés: Mekkora az amplitúdója, vagyis a legnagyobb értéke az \(\displaystyle x(t)\) függvénynek? Erre pl. a rezgőmozgás ismert sebességképletének felírásával kaphatunk választ. \(\displaystyle x(t)\) legnagyobb értékénél a változási sebessége nulla:
\(\displaystyle \dot{x}(t)=-A_1\omega\sin\omega t+A_2\omega\cos\omega t=0,\qquad\textrm{azaz}\qquad\tg\omega t=\frac{A_2}{A_1}.\)
Ezt (17)-be helyettesítve kapjuk, hogy
\(\displaystyle x_\mathrm{max}=\sqrt{A_1^2+A_2^2}.\)
Megjegyzés. Ugyanezt az eredményt egyszerű geometriai megfontolással is megkaphatjuk. Ha ugyanis egy \(\displaystyle A_1\) és \(\displaystyle A_2\) oldalélű téglalapot az egyik csúcspontja körül függőleges síkban megforgatunk (6. ábra), a szemközti csúcsa akkor kerül a legmagasabbra, amikor éppen a forgástengely fölé ér, és ekkor a magassága
\(\displaystyle x_\mathrm{max}=\sqrt{A_1^2+A_2^2}.\)
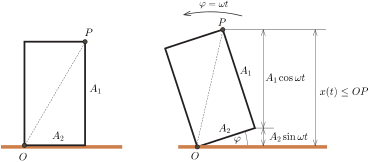
6. ábra
A feladat eredeti kérdésében szereplő amplitúdó tehát (18) felhasználásával
\(\displaystyle A=\sqrt{A_1^2+A_2^2}=\frac{a}{\omega^2}\sqrt{\left(\cos\omega\tau-1\right)^2+\sin^2\omega\tau}=\frac{a}{\omega^2}\sqrt{2\left(1-\cos\omega\tau\right)}.\)
Megjegyzés. A fenti megoldásban szerepló \(\displaystyle x(t;t')\) függvényt a vizsgált probléma Green-függvényének nevezik. A George Green (1793-1841) angol matematikus által kidolgozott módszert sikeresen alkalmazzák az elméleti fizika számos területén.
Statisztika:
30 dolgozat érkezett. 6 pontot kapott: Beke Márton Csaba, Elekes Panni, Erdélyi Dominik, Gyenes Károly, Kossár Benedek Balázs, Mezei Marcell, Mi Feiyu, Murányi Nimród Máté, Qinyu Yue, Rajtik Sándor Barnabás, Simon János Dániel, Tajta Sára, Tóth Hanga Katalin, Vigh István Csaba, Winhoffer Júlia, Zádori Gellért, Zólomy Csanád Zsolt. 5 pontot kapott: Hornyák Zalán Zétény, Kovács Tamás , Kovács Tamás, Papp Emese Petra, Tasnádi Zsófia. 4 pontot kapott: 2 versenyző. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2025. októberi fizika feladatai

