A KöMaL 2019. szeptemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2019. október 10-én LEJÁRT. |
M. 388. Vizsgáljuk meg, hogy egy (rövidáruboltban kapható) gumiszál (vagy gumiszalag) mennyire követi a lineáris erőtörvényt! Mérjük meg a gumiszál hosszát növekvő és csökkenő terhelés esetén is!
Közli: Nagy Piroska Mária, Budapest
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2019. október 10-én LEJÁRT. |
G. 677. Egyenletesen lépegetünk másodpercenként egyet. Minden lépésünk 0,5 m hosszú. Mozgásunk a következő szabályt követi: egyet lépünk előre, kettőt hátra, majd hármat előre, négyet hátra, azután ötöt előre, hatot hátra és így tovább.
\(\displaystyle a)\) Hol leszünk egy perc múlva?
\(\displaystyle b)\) Mennyi a sebességnagyságunk átlaga?
\(\displaystyle c)\) Mennyi a sebességvektorunk átlagos értéke?
(3 pont)
G. 678. Egy autó 36 km/h sebességgel halad a városban, miközben kerekei tisztán gördülnek. Mekkora a kerék legelöl lévő pontjának a talajhoz viszonyított sebessége?
(3 pont)
G. 679. Egy tartályban lévő gáz nyomását U alakú csőben lévő higany segítségével mérjük meg az ábrán látható módon.
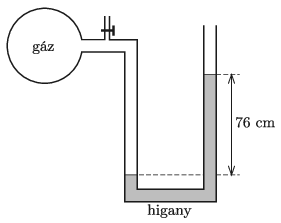
\(\displaystyle a)\) Mekkora a gáz abszolút nyomása, ha az U alakú cső két szárában a higanyszintek különbsége 76 cm, továbbá a külső légnyomás 1 atm?
\(\displaystyle b)\) Ezután a gázt teljesen kiszivattyúzzuk a tartályból az ábrán látható csaphoz csatlakoztatott szivattyú segítségével. Hogyan helyezkedik el ekkor a higany?
(3 pont)
G. 680. Egyszerre megrántjuk egy kifeszített gumikötél mindkét végét, az egyiket felfelé, a másikat lefelé. Így két hullám indul el egymás felé az ábrán látható módon.

A két szimmetrikus hullám azonos nagyságú energiát szállít. A két jel találkozásakor a gumikötél egy pillanatra egyenessé válik. Hová tűnik ekkor a két hullám energiája? Áthaladnak-e egymáson a jelek, vagy végleg kioltják egymást?
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2019. október 10-én LEJÁRT. |
P. 5143. Lehet-e olyan sötét éjszaka a Holdon, hogy csak a csillagok világítanak
\(\displaystyle a)\) a Hold felénk eső oldalán, illetve
\(\displaystyle b)\) a Hold túlsó oldalán?
Közli: Vladár Károly, Kunfehértó
(4 pont)
P. 5144. Egy \(\displaystyle \alpha\) hajlásszögű lejtő síkjára merőlegesen tartórudat rögzítünk. A rúd tetejéhez hozzáerősítjük egy \(\displaystyle \ell\) hosszúságú fonálinga felső végpontját. Az inga fonala \(\displaystyle \beta\) szöget zár be a lejtő síkjával.
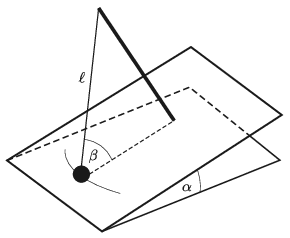
Mekkora az inga kis amplitúdójú lengéseinek periódusideje, ha \(\displaystyle \alpha+\beta < 90^\circ\), és a súrlódás elhanyagolható?
(4 pont)
P. 5145. A vissza nem térő üstökösök többsége közvetlenül a Naprendszer legkülső tartományából, az ún. Oort-felhőből kerül a Naprendszer belsejébe. Adjunk becslést arra, hogy mennyi ideig tart ez az út! A Nap körül szimmetrikusan, gömbhéj alakban elhelyezkedő Oort-felhő átmérője \(\displaystyle 70\,000\) csillagászati egység. Tegyük fel, hogy az üstökös aphéliuma (a Naptól való legnagyobb távolsága) az Oort-felhő sugarával egyezik meg.
Csillagászati olimpiai feladat
(4 pont)
P. 5146. Egy üvegpohárban a víz felülete a pohár falánál homorú, a higany felülete viszont domború. Létezik-e olyan alakú üvegedény, amelynek falánál a higany felülete is homorú?
(4 pont)
P. 5147. A Pécs–Pogány Repülőtéren repülőnapot rendeznek. Reklám céljából egy \(\displaystyle V=10~\rm m^3\) térfogatú, héliummal töltött ballont engednek a magasba súlytalannak tekinthető kötélen. A ballon anyagának térfogata elhanyagolható, töltetlen tömege \(\displaystyle m=2~\rm kg\). A hőmérséklet a ballon belsejében, illetve annak külső környezetében \(\displaystyle T=300\) K, a külső légnyomás \(\displaystyle p_0=10^5\) Pa. A ballon anyagának rugalmasságából származó nyomástól eltekintünk.
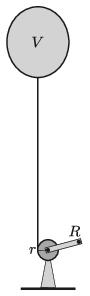
A rendezvény végén a ballont csörlővel lassan levonják. A csörlő hengerének sugara \(\displaystyle r=10\) cm, a hajtókar sugara \(\displaystyle R=30\) cm. A közegellenállás elhanyagolható.
\(\displaystyle a)\) Mekkora erőt kell a hajtókarra kifejteni a ballon egyenletes lehúzása esetén?
\(\displaystyle b)\) Mekkora teljesítmény szükséges a levonáshoz, ha a ballon \(\displaystyle v=1\) m/s sebességgel süllyed?
Párkányi László fizikaverseny, Pécs
(4 pont)
P. 5148. Egy 1 méter hosszúságú, hengeres tartályban levegő van bezárva. A tartályt a vízszintes hossztengelye irányában állandó gyorsulással mozgatjuk, miközben a bezárt levegő hőmérsékletét mindvégig állandó, \(\displaystyle T=273\) K értéken tartjuk. Mekkora \(\displaystyle a_0\) gyorsulásnál lenne a tartály elején a levegő nyomása
\(\displaystyle a)\) 0,1%-kal kisebb,
\(\displaystyle b)\) fele akkora,
mint a tartály hátulján?
Útmutatás: ha a hőmérséklet állandó lenne, a földi légkör sűrűsége a barometrikus magasságformula szerint változna: \(\displaystyle \varrho(h)= \varrho_0{\rm e}^{-\frac{Mgh}{RT}}\), ahol \(\displaystyle M\) a levegő átlagos móltömege.
Közli: Vass Miklós, Budapest
(5 pont)
P. 5149. Egy fizikatanár röpdolgozatot írat két csoportban. Az egyik csoport feladata a következő: ,,Mekkora beesési szögű az a vékony fénysugár, ami gömb alakú vízcseppbe lépve szabályos háromszög mentén jár körbe?'' A másik csoport ugyanezt a feladatot kapja, de ekkor szabályos négyszög, vagyis egy négyzet oldalélei mentén kell haladnia a fénysugárnak. Feladhatja-e a tanár ugyanezt a példát a pótdolgozatban szabályos ötszöggel? Határozzuk meg a beesési szögeket az egyes esetekben! (A víz törésmutatója \(\displaystyle \frac43\).)
Közli: Honyek Gyula, Veresegyház
(4 pont)
P. 5150. Két teljesen egyforma, \(\displaystyle n=1{,}5\) törésmutatójú üvegből készített síkdomború, vékony lencse közül az egyiknek a sík, a másiknak a domború felületét tesszük tükrözővé. Mekkora az így kapott két leképező eszköz fókusztávolságának aránya?
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 5151. Homogén elektrosztatikus erőtérben egy \(\displaystyle AB\) egyenes szakaszon a mérések szerint a potenciál értéke az \(\displaystyle A\)-tól vett \(\displaystyle x\) távolság függvényében:
| \(\displaystyle x~[\mathrm{cm}]\) | 2 | 3 | 4 | 5 | 6 |
| \(\displaystyle U~[\mathrm{V}]\) | 130 | 150 | 180 | 210 | 230 |
Határozzuk meg közelítőleg a térerősség \(\displaystyle AB\) menti komponensének nagyságát!
Közli: Radnai Gyula, Budapest
(4 pont)
P. 5152. Mennyi a valószínűsége, hogy a 131-es jód egy atomja a következő percben elbomlik? (A felezési idő: \(\displaystyle T_{1/2}=8\) nap.)
Közli: Légrádi Imre, Sopron
(4 pont)
P. 5153. Két egyforma, homogén rúd egy-egy végpontja csuklósan kapcsolódik egymáshoz. A rudak vízszintes, súrlódásmentes asztallapon egy egyenes mentén nyugszanak. Az egyik rúd szabad végére a rúdra merőleges irányban hirtelen ráütünk, mire az a pont 1 m/s sebességgel kezd el mozogni. Milyen irányban és mekkora sebességgel indul el a másik rúd szabad végpontja?
Közli: Gnädig Péter, Vácduka
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
