A KöMaL 2020. szeptemberi matematika feladatai

K-jelű feladatok A beküldési határidő 2020. október 12-én LEJÁRT.

K. 659. Hány olyan különböző négyszög van, amelynek csúcsai egy adott szabályos kilencszög csúcsai közül valók és a négyszög a belsejében tartalmazza a kilencszög középpontját? (Az egybevágó négyszögeket nem tekintjük különbözőnek.)

(6 pont)

megoldás, statisztika

K. 660. Az ábrán látható négyzeteket kitöltöttük az 1, 2, 3, 4, 5, 6, 7, 8 és 9 számokkal, majd a négyzetek közötti körökbe beírtuk mindenhol a két szomszédos négyzetbe írt szám összegét. Ezután néhány körből a benne lévő számot kiradíroztuk, a négyzeteket pedig besatíroztuk.

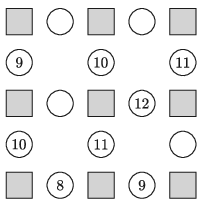
\(\displaystyle a)\) Melyik számokat radíroztuk ki az üres körökből?

\(\displaystyle b)\) Írjuk be mindegyik négyzetbe azt a számot, amit eredetileg beleírtunk.

(6 pont)

megoldás, statisztika

K. 661. Az \(\displaystyle ABCDEFGH\) szabályos nyolcszög 2 egység hosszú \(\displaystyle BC\) és \(\displaystyle GH\) oldalára a \(\displaystyle BCIM\) és a \(\displaystyle GHNP\) négyzetet rajzoljuk befelé. Igazoljuk, hogy az \(\displaystyle N\) és \(\displaystyle M\) pontok egybeesnek.

(6 pont)

megoldás, statisztika

K. 662. Egy sorozat első négy tagja 1-es. Az ötödik tagtól kezdve minden tag értékét úgy kapjuk, hogy a hárommal és a néggyel előtte álló tagot összeadjuk. Hány páros szám van a sorozat első 150 tagja között?

(6 pont)

megoldás, statisztika

K. 663. Öt egymást követő egész számra igaz, hogy az első három négyzetének összege megegyezik az utolsó kettő négyzetének összegével. Melyek lehetnek ezek a számok?

(6 pont)

megoldás, statisztika

C-jelű feladatok A beküldési határidő 2020. október 12-én LEJÁRT.

C. 1616. Oldjuk meg az

\(\displaystyle x+\frac{1}{y+\frac{1}{\frac{5z}{4}+\frac{13}{6v}}}=\frac{135}{113} \)

egyenletet, ha \(\displaystyle x\), \(\displaystyle y\), \(\displaystyle z\), \(\displaystyle v\) pozitív egész számok.

Javasolta: Bíró Bálint (Eger)

(5 pont)

megoldás, statisztika

C. 1617. Elhelyezhető-e átfedés nélkül négy darab \(\displaystyle 2\times 8\)-as téglalap egy \(\displaystyle 7\times15\)-ös téglalap belsejében az ábrán látható elrendezésben? (Az ábra nem arányos.)

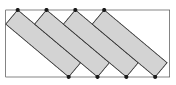
(5 pont)

megoldás, statisztika

C. 1618. Bizonyítsuk be, hogy az \(\displaystyle a_n=\frac{(n-1)n}{n+1}\) sorozat elemeire \(\displaystyle n\ge 1\) esetén fennáll:

\(\displaystyle \frac23\le a_{n+1}-a_n<1. \)

(5 pont)

megoldás, statisztika

C. 1619. Egy hegyesszögű háromszög mindhárom oldalfelező pontjából merőlegest állítunk a másik két oldalra. Bizonyítsuk be, hogy a behúzott szakaszok által meghatározott hatszög területe a háromszög területének felével egyenlő.

(Horvát feladat)

(5 pont)

megoldás, statisztika

C. 1620. Mekk Elek, az ezermester egy ugródeszkát eszkábált az udvarára. Mérései alapján megállapította, hogy ha a róla való elugráshoz a deszka vége az alaphelyzet alá hajlik \(\displaystyle x\) dm-rel, akkor a deszkáról \(\displaystyle 0{,}5x^2+ax+b\) dm magasra tud ugrani. Sajnos \(\displaystyle a\) és \(\displaystyle b\) értékét elfelejtette, azonban arra emlékszik, hogy ha \(\displaystyle 10\) cm-t hajlott le a deszka, akkor \(\displaystyle 35\) cm magasra ugrott, négyszer ekkora lehajlásnál pedig négyszer ekkorát ugrott. Milyen \(\displaystyle a\), illetve \(\displaystyle b\) értékeket határozott meg Mekk Elek?

(5 pont)

megoldás, statisztika

C. 1621. Egy érintőtrapéz oldalainak mérőszámai egész számok, melyek valamilyen sorrendben egy számtani sorozat szomszédos elemeit képezik. Tudjuk, hogy a beírható körének sugara és a rövidebbik alapja egyaránt 6. Mekkora a másik három oldala?

Javasolta: Németh László (Fonyód)

(5 pont)

megoldás, statisztika

C. 1622. Bizonyítsuk be, hogy az \(\displaystyle y=1-|x-1|\) és az \(\displaystyle y=|2x-a|\) függvények grafikonja által közrezárt alakzat területe kisebb, mint \(\displaystyle \frac13\), ha \(\displaystyle 1<a<2\).

(

Horvát feladat)

(5 pont)

megoldás, statisztika

B-jelű feladatok A beküldési határidő 2020. október 12-én LEJÁRT.

B. 5110. Egy egyenlő szárú háromszögbe írható körnek az oldalakkal párhuzamos érintői a háromszögből három kis háromszöget vágnak le. Bizonyítsuk be, hogy az alapra illeszkedő kis háromszögek alaphoz tartozó magassága megegyezik a háromszögbe írható kör sugarával.

(3 pont)

megoldás, statisztika

B. 5111. Az \(\displaystyle a\) és \(\displaystyle b\) valós számokról tudjuk, hogy \(\displaystyle a + b = 1\) és \(\displaystyle a^2 + b^2 = 2\). Határozzuk meg \(\displaystyle a^8 + b^8\) értékét.

Szalai Máté (Szeged) javaslata alapján

(3 pont)

megoldás, statisztika

B. 5112. Egy kártyapakliban \(\displaystyle p\) darab piros és \(\displaystyle k\) darab kék kártya van. Hányféleképpen választhatunk ki a pakliból kártyákat úgy, hogy a piros kártyák száma \(\displaystyle n\)-nel több legyen, mint a kék kártyák száma?

(4 pont)

megoldás, statisztika

B. 5113. Legyenek \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle c\) adott, páronként relatív prím pozitív egészek. Igazoljuk, hogy ekkor az

\(\displaystyle x^a + y^b=z^c \)

egyenletnek végtelen sok megoldása van az \(\displaystyle (x,y,z)\) pozitív egész számhármasok körében.

(5 pont)

megoldás, statisztika

B. 5114. Az \(\displaystyle ABCDEFGH\) egységkockát elmetszettük egy síkkal úgy, hogy az \(\displaystyle AB\) és \(\displaystyle AD\) éleket az \(\displaystyle A\)-tól azonos, \(\displaystyle x\) távolságra levő \(\displaystyle P\) és \(\displaystyle Q\) belső pontjaikban, a \(\displaystyle BF\) élt pedig az \(\displaystyle R\) pontban metszi. Mekkora a \(\displaystyle BR\) távolság, ha \(\displaystyle QPR\sphericalangle=120^\circ\)?

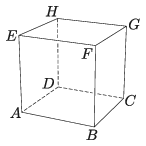
(4 pont)

megoldás, statisztika

B. 5115. Ali erszényében \(\displaystyle n\) darab érme lapul, Babának pedig van \(\displaystyle n-1\) darab, kezdetben üres erszénye. Baba a következő játékot játssza: a kezdetben egy erszényben lévő érméket szétosztja két erszénybe, egyikbe \(\displaystyle a_1\), másikba \(\displaystyle b_1\) érmét téve (\(\displaystyle a_1,b_1>0\)), és a táblára felírja az \(\displaystyle a_1b_1\) szorzatot. Majd innentől (az előzőhöz hasonlóan) a \(\displaystyle k\)-adik lépésben (\(\displaystyle k=2,3,\ldots\)) kiválaszt egy legalább két érmét tartalmazó erszényt, a benne lévő érméket szétosztja két üres erszénybe, egyikbe \(\displaystyle a_k\), másikba \(\displaystyle b_k\) érmét téve (\(\displaystyle a_k,b_k>0\)), és a táblára felírja az \(\displaystyle a_kb_k\) szorzatot.

A játék akkor ér véget, ha minden erszénybe 1-1 érme került. Ekkor Ali kiszámolja a táblán lévő \(\displaystyle a_k b_k\) szorzatok összegét és ennyi aranyat ad Babának.

Legfeljebb mennyi aranyat kaphat Baba?

(5 pont)

megoldás, statisztika

B. 5116. Legyen \(\displaystyle a,b,c>0\) és \(\displaystyle x,y,z\ge 0\). Igazoljuk, hogy ha \(\displaystyle x+aby \le a(y+z)\), \(\displaystyle y+bcz \le b(z+x)\), és \(\displaystyle z+cax \le c(x+y)\), akkor \(\displaystyle x=y=z=0\) vagy \(\displaystyle a=b=c=1\).

Javasolta: George Stoica (Saint John, Kanada)

(6 pont)

megoldás, statisztika

B. 5117. Az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) pontok (ebben a sorrendben) egy egyenesre esnek. Az \(\displaystyle AB\), \(\displaystyle BC\) és \(\displaystyle CD\) szakaszokra (azonos félsíkban) emelt szabályos háromszögek harmadik csúcsai legyenek rendre \(\displaystyle E\), \(\displaystyle F\), illetve \(\displaystyle G\). Jelöljük az egyenesen szomszédos pontok távolságát a következőképpen: \(\displaystyle AB=a\), \(\displaystyle BC=b\), \(\displaystyle CD=c\). Mutassuk meg, hogy az \(\displaystyle EFG \sphericalangle \) akkor és csak akkor \(\displaystyle 120^{\circ}\)-os, ha \(\displaystyle a+c=b\) vagy \(\displaystyle \frac1a+\frac1c=\frac1b\).

(6 pont)

megoldás, statisztika

A-jelű feladatok A beküldési határidő 2020. október 12-én LEJÁRT.

A. 780. Egy \(\displaystyle n\times n\)-es táblázatot kiszíneztünk úgy, hogy minden \(\displaystyle 2\times 2\)-es részben legyen legalább két azonos színű mező. Legfeljebb hány színt használhattunk a színezésben?

A Dürer-verseny feladata alapján

(7 pont)

statisztika

A. 781. Szeretnénk körzővel és vonalzóval megszerkeszteni egy egyenlő szárú háromszöget. Ehhez a következő négy adatból kapunk meg kettőt: a háromszög alapjának hossza (\(\displaystyle a\)), a háromszög szárának hossza (\(\displaystyle b\)), a beírt körének sugara (\(\displaystyle r\)), a körülírt körének sugara (\(\displaystyle R\)). A hat lehetséges esetből melyek azok, amikor a háromszög biztosan megszerkeszthető?

Rubóczky György (Budapest) ötlete alapján

(7 pont)

statisztika

A. 782. Bizonyítsuk be, hogy egy síkbarajzolható egyszerű gráf éleit mindig lehet úgy irányítani, hogy minden pont kifoka legfeljebb három legyen.

Angol versenyfeladat

(7 pont)

statisztika