A KöMaL 2021. novemberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2021. december 10-én LEJÁRT. |
K. 704. Egy sakkversenyen 5 játékos vett részt. Mindenki egyszer játszott mindenkivel, a győzelemért 1 pont, döntetlenért 0,5 pont, vereségért 0 pont járt. A verseny végére az derült ki, hogy:
– az első helyezettnek nem volt döntetlenje;
– a második helyezett nem vesztett játszmát;
– minden versenyzőnek különböző pontszáma lett.
Hány pontot értek el az egyes helyezettek?
(5 pont)
K. 705. Az 1, 2, 3, 4, 5, 6, 7, 8 számok közül kiválasztunk három különböző számot és összeadjuk őket. Ezt minden lehetséges számhármassal megtesszük. Az összeadások között lesznek páros és páratlan eredményűek. Melyikből lesz több, a páros vagy a páratlan eredményűből?
(5 pont)
K. 706. Egy három oszlopból álló táblázat első sorába beírtunk 3 számot balról jobbra haladva, nevezzük ezeket \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\)-nek. A második sorba az \(\displaystyle a-b\), \(\displaystyle b-c\), \(\displaystyle c-a\) számok kerülnek. A harmadik sorba a második sor elemeiből ugyanezen szabály szerint előállított számok kerülnek (az első, második és harmadik helyen álló számokkal végzett műveleteket tekintve), és így folytatjuk tovább a táblázat kitöltését. Mutassuk meg, hogy a táblázatban a negyedik sortól kezdve nem fordulhat elő a 2021.
(5 pont)
 |
K/C-jelű feladatokA beküldési határidő 2021. december 10-én LEJÁRT. |
K/C. 707. Néhány (legalább kettő) gyerek körbeáll, és ,,kiesős'' játékot játszik. Ebben a játékban a kezdő játékostól kezdve minden második gyerek kiesik, és kiáll a körből, az utolsóként bent maradó játékos győz. Például, ha hatan játszanak (A, B, C, D, E, F) és A kezd, akkor B, D, F, C, A sorrendben állnak ki, így E a győztes. Hány gyerek esetén lehet győztes a kezdő játékos?
(5 pont)
K/C. 708. Jean, az inas azt a feladatot kapja gazdájától, hogy tegyen gyertyákat a nappaliban levő 10 darab háromágú gyertyatartóba. Jeannak ezt úgy kell megoldania, hogy vagy minden gyertyatartóban 3 különböző színű gyertya legyen, vagy mind a 30 gyertya ugyanolyan színű. Jean bemegy a sarki vegyesboltba, ahol összesen 70 db gyertyát talál. Mutassuk meg, hogy ebből mindenképpen tud 30 db-ot vásárolni úgy, hogy a feltételeknek megfelelően feltölthesse a gyertyatartókat.
(5 pont)
 |
C-jelű feladatokA beküldési határidő 2021. december 10-én LEJÁRT. |
C. 1689. Oldjuk meg a következő egyenletrendszert, ha \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\) egész számok:
$$\begin{align*} a + d & = 9,\\ ad + b & = 8,\\ bd + c & = 74,\\ cd & = 18. \end{align*}$$Javasolta: Berkó Erzsébet (Szolnok)
(5 pont)
C. 1690. Az \(\displaystyle AB\) szakasz fölé rajzolt egységsugarú félkör középpontja \(\displaystyle O\). Megrajzoljuk a félkör belsejébe a \(\displaystyle K\) középpontú, \(\displaystyle OB\) átmérőjű félkört, amelyet az \(\displaystyle A\) pontból induló félegyenes a \(\displaystyle C\) pontban érint. Az \(\displaystyle O\) pontból az \(\displaystyle AC\)-re bocsátott merőleges az \(\displaystyle AB\) átmérőjű félkörvonalat a \(\displaystyle D\) pontban metszi. Bizonyítsuk be, hogy a \(\displaystyle BD\) szakasz felezőpontja \(\displaystyle C\).
(5 pont)
C. 1691. Határozzuk meg, mely \(\displaystyle p\), \(\displaystyle q\) pozitív prímszámokra teljesül, hogy \(\displaystyle p^{5}-q^{3}+{(p+q)}^{4}=9900\).
(5 pont)
C. 1692. Az \(\displaystyle ABCD\) négyzet \(\displaystyle DA\) oldalának belső pontja \(\displaystyle P\). A \(\displaystyle PBC\sphericalangle\)-et felező egyenes a \(\displaystyle CD\) oldalt a \(\displaystyle Q\) pontban metszi, a \(\displaystyle Q\) pontból a \(\displaystyle BP\) egyenesre bocsátott merőleges talppontja \(\displaystyle R\). Határozzuk meg az \(\displaystyle AR\) és \(\displaystyle BQ\) egyenesek hajlásszögét.
(5 pont)
C. 1693. Egy kocka csúcsai közül véletlenszerűen kiválasztunk négyet. Bármely négy csúcsot ugyanakkora valószínűséggel választunk ki. Mekkora az esélye, hogy a négy csúcs tetraédert határoz meg? Mi a valószínűsége, hogy a négy pont egy szabályos tetraéder négy csúcsa?
Javasolta: Zagyva Tiborné (Baja)
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2021. december 10-én LEJÁRT. |
B. 5198. Ha az asztalom tetejére teszem a teknősömet, akkor a földön álló macskám fejéhez képest a teknős feje 70 cm-rel van feljebb. Ha a macskámat teszem az asztal tetejére, akkor a földön álló kutyám fejéhez képest 80 cm-rel lesz magasabban a macska feje. Ha pedig a kutyámat teszem az asztalra, akkor a földön álló teknőshöz képest 120 cm-rel lesz magasabban a kutya feje. Hány cm magas az asztalom?
Kocsis Szilveszter (Budapest) ötlete alapján
(3 pont)
B. 5199. Egy sakktábla minden mezőjére egy érmét teszünk Fejjel felfelé. Megengedett lépés, hogy három közvetlenül egymás mellett lévő érmét egy sorban vagy egy oszlopban egyszerre megfordítsunk. El lehet-e érni azt, hogy minden érme Írással legyen felfelé?
Javasolta: Gáspár Merse Előd (Budapest)
(4 pont)
B. 5200. Az \(\displaystyle A_0A_1=1\) átmérőjű félkörvonalon felvesszük az \(\displaystyle A_2\) pontot úgy, hogy \(\displaystyle A_0A_1A_2\sphericalangle=1^\circ\). Ezután a körvonal \(\displaystyle A_1A_2\) ívén felvesszük az \(\displaystyle A_3\) pontot úgy, hogy \(\displaystyle A_1A_2A_3\sphericalangle=2^\circ\). Ezt folytatjuk a következők szerint: az \(\displaystyle A_{k+1}\) pontot a körvonal \(\displaystyle A_{k-1}A_k\) ívén választjuk úgy, hogy \(\displaystyle A_{k-1}A_kA_{k+1}\) szög \(\displaystyle k\) fok (\(\displaystyle k=3,4,\ldots,9\)). Milyen hosszú az \(\displaystyle A_9A_{10}\) szakasz? (Az ábra tájékoztató jellegű.)
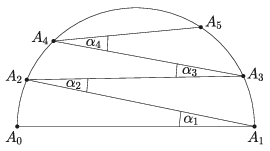
(3 pont)
B. 5201. Legyenek az \(\displaystyle n\) pozitív egész szám pozitív osztói \(\displaystyle 1=d_1<d_2<\ldots< d_k=n\). Határozzuk meg azokat az összetett \(\displaystyle n\) számokat, amelyekre \(\displaystyle d_1\), \(\displaystyle d_1+d_2\), \(\displaystyle d_1+d_2+d_3\), \(\displaystyle \ldots,\) \(\displaystyle d_1+d_2+\ldots+d_{k-1}\) számok mind osztói \(\displaystyle n\)-nek.
Javasolta: Sándor Csaba (Budapest)
(4 pont)
B. 5202. Két racionális számot ismerősnek nevezünk, ha van olyan \(\displaystyle p/q\), illetve \(\displaystyle r/s\) alakjuk (\(\displaystyle p\), \(\displaystyle q\), \(\displaystyle r\), \(\displaystyle s\) egészek), amelyekre \(\displaystyle |ps-qr|=1\). Hány közös ismerőse lehet két ismerős racionális számnak?
Javasolta: Kocsis Szilveszter (Budapest)
(5 pont)
B. 5203. Az \(\displaystyle ABC\) háromszögben \(\displaystyle AB>BC\), a beírt kör érintési pontjai a \(\displaystyle BC\), \(\displaystyle CA\) és \(\displaystyle AB\) oldalakon rendre \(\displaystyle A_0\), \(\displaystyle B_0\) és \(\displaystyle C_0\), továbbá az \(\displaystyle AC\) oldalhoz írt kör az \(\displaystyle AC\) oldalt a \(\displaystyle B_1\) pontban érinti. Mutassuk meg, hogy az \(\displaystyle A_0B_1\) és \(\displaystyle B_0C_0\) szakaszok metszéspontja akkor és csak akkor van rajta a \(\displaystyle B\) csúcsból induló belső szögfelezőn, ha a \(\displaystyle C\) csúcsnál lévő szög \(\displaystyle 90^{\circ}\).
Javasolta: Holló Gábor (Budapest)
(5 pont)
B. 5204. Legyenek \(\displaystyle 1\le a,b,c,d\le 4\) valós számok. Bizonyítsuk be, hogy
\(\displaystyle 16\le (a+b+c+d)\left(\frac{1}a+\frac{1}b+\frac{1}c+\frac{1}d\right)\le 25. \)
Javasolta: Szoldatics József (Budapest)
(6 pont)
B. 5205. Adott a síkon négy kör: a \(\displaystyle k_1\) kör belsejében a \(\displaystyle k_2\), a \(\displaystyle k_2\) belsejében a \(\displaystyle k_3\), és a \(\displaystyle k_3\) belsejében a \(\displaystyle k_4\) kör. Adott továbbá három egyenes, \(\displaystyle e_1\), \(\displaystyle e_2\) és \(\displaystyle e_3\), amelyek közül semelyik kettő sem párhuzamos, és mind a négy kört metszik. Mindegyik \(\displaystyle i=1,2,3\) esetén legyenek az \(\displaystyle e_i\) egyenes metszéspontjai a körökkel \(\displaystyle A_i\), \(\displaystyle B_i\), \(\displaystyle C_i\), \(\displaystyle D_i\), \(\displaystyle E_i\), \(\displaystyle F_i\), \(\displaystyle G_i\) és \(\displaystyle H_i\), ebben a sorrendben. Igazoljuk, hogy ha \(\displaystyle A_1B_1+E_1F_1=C_1D_1+G_1H_1\) és \(\displaystyle A_2B_2+E_2F_2=C_2D_2+G_2H_2\), akkor \(\displaystyle A_3B_3+E_3F_3=C_3D_3+G_3H_3\).
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2021. december 10-én LEJÁRT. |
A. 809. Az \(\displaystyle ABC\) háromszög oldalai a szokásos jelölésekkel \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle c\), a súlypontja pedig \(\displaystyle S\). Igazoljuk, hogy a háromszög síkjának tetszőleges \(\displaystyle P\) pontjára teljesül, hogy
\(\displaystyle a\cdot PA^3+b\cdot PB^3+c\cdot PC^3\ge 3abc\cdot PS. \)
Javasolta: Shultz János (Szeged)
(7 pont)
A. 810. Legyen minden pozitív egész \(\displaystyle n\)-re
\(\displaystyle r_n=\sum_{t=0}^{n} {(-1)}^t \binom{n}{t} \frac{1}{(t+1)!}. \)
Bizonyítsuk be, hogy \(\displaystyle \sum_{n=1}^{\infty} r_n=0\).
(7 pont)
A. 811. Adott egy \(\displaystyle n\) elemű \(\displaystyle A\) halmaz és egy \(\displaystyle k<n\) pozitív egész szám. Határozzuk meg \(\displaystyle m\) legnagyobb lehetséges értékét, ha \(\displaystyle i=1,2,\ldots,m\) esetén kiválaszthatók \(\displaystyle B_i\) és \(\displaystyle C_i\) halmazok úgy, hogy a következők teljesüljenek:
\(\displaystyle (i)\) \(\displaystyle B_i \subset A\), \(\displaystyle |B_i|=k\),
\(\displaystyle (ii)\) \(\displaystyle C_i \subset B_i\) (\(\displaystyle C_i\) elemszámára nincs további megkötés),
\(\displaystyle (iii)\) minden \(\displaystyle i \ne j\) esetén \(\displaystyle B_i \cap C_j \ne B_j \cap C_i\).
Javasolta: Imolay András (Budapest)
(7 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

