A C. 1690. feladat (2021. november)

C. 1690. Az \(\displaystyle AB\) szakasz fölé rajzolt egységsugarú félkör középpontja \(\displaystyle O\). Megrajzoljuk a félkör belsejébe a \(\displaystyle K\) középpontú, \(\displaystyle OB\) átmérőjű félkört, amelyet az \(\displaystyle A\) pontból induló félegyenes a \(\displaystyle C\) pontban érint. Az \(\displaystyle O\) pontból az \(\displaystyle AC\)-re bocsátott merőleges az \(\displaystyle AB\) átmérőjű félkörvonalat a \(\displaystyle D\) pontban metszi. Bizonyítsuk be, hogy a \(\displaystyle BD\) szakasz felezőpontja \(\displaystyle C\).

(5 pont)

A beküldési határidő 2021. december 10-én LEJÁRT.

1. megoldás. Tekintsük az alábbi ábrát, amelyen az \(\displaystyle AC\)-re merőleges \(\displaystyle OD\) egyenes talppontját \(\displaystyle E\)-vel, az \(\displaystyle AC\) egyenesnek a nagyobbik félkörrel való metszéspontját \(\displaystyle F\)-fel jelöltük. A \(\displaystyle C\) pontot összekötöttük a kisebb félkör \(\displaystyle K\) középpontjával.

Az \(\displaystyle ABF\) és \(\displaystyle OBC\) háromszögek Thalész tétele miatt az \(\displaystyle F\), illetve \(\displaystyle C\) pontban derékszögű háromszögek. A két derékszögű háromszög körülírt körének sugara \(\displaystyle OA=OB=OD=1\), illetve \(\displaystyle KO=KB=KC=\frac{1}{2}\). Tudjuk, hogy a kisebb félkörben a \(\displaystyle KC\) sugár a \(\displaystyle C\) pontban merőleges a félkör \(\displaystyle AF\) érintőjére, és ezért \(\displaystyle OE\parallel{KC}\parallel{BF}\). Ez pedig azt jelenti, hogy \(\displaystyle OBFE\) derékszögű trapéz, amelynek \(\displaystyle KC\) a középvonala, és így egyrészt \(\displaystyle C\) felezi a trapéz \(\displaystyle EF\) szárát, másrészt \(\displaystyle KC=\frac{OE+BF}{2}\), azaz

\(\displaystyle 1=2KC=OE+BF.\)

Mivel \(\displaystyle OE+DE=1\) szintén igaz, ezért azt kapjuk, hogy \(\displaystyle DE=BF\). A \(\displaystyle CDE\) és \(\displaystyle CBF\) derékszögű háromszögekben tehát a \(\displaystyle DE\) és \(\displaystyle BF\), illetve \(\displaystyle CE\) és \(\displaystyle CF\) befogók egyenlők, ezért a két derékszögű háromszög egybevágó. Ekkor az átfogóik is egyenlő hosszúak, azaz \(\displaystyle BC=DC\). A két háromszög egybevágósága miatt \(\displaystyle BCF\sphericalangle=DCE\sphericalangle\), és ez csakis úgy lehetséges, ha a \(\displaystyle B,C\) és \(\displaystyle D\) pontok egy egyenesen vannak, és így a \(\displaystyle BD\) szakasz felezőpontja valóban \(\displaystyle C\).

2. megoldás. Az ehhez a megoldáshoz használt ábrán jelöléseink az előző megoldás ábrájának megfelelőek, az \(\displaystyle OBC\sphericalangle\)-et \(\displaystyle \beta\)-val jelöltük.

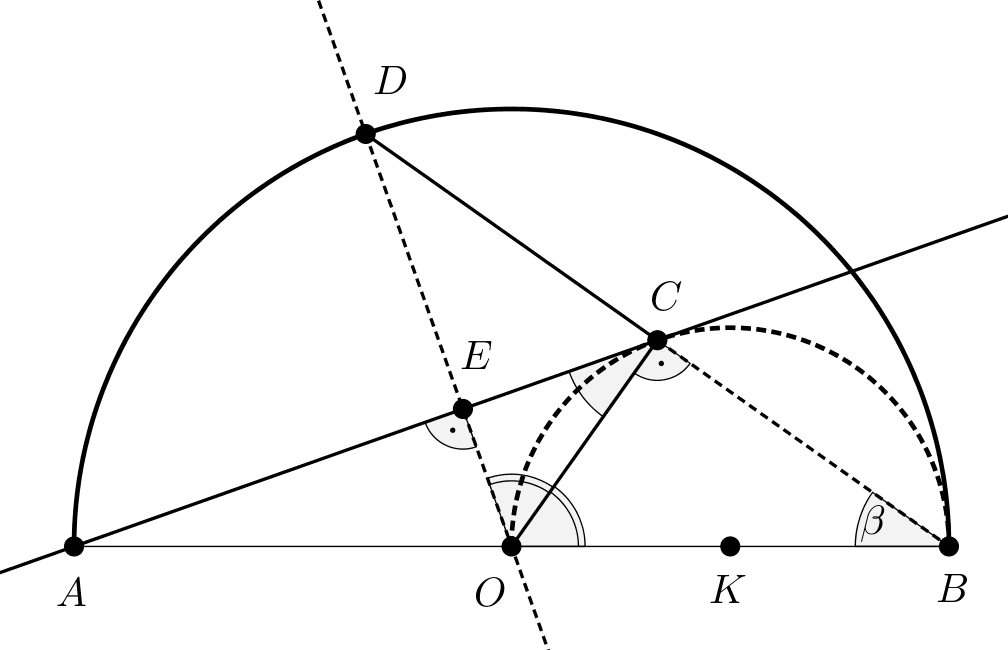
Thalész tétele miatt az \(\displaystyle OBC\) háromszög derékszögű, amelynek átfogója \(\displaystyle OB\).

Az \(\displaystyle OBC\) derékszögű háromszögben ezért \(\displaystyle COB\sphericalangle=90^{\circ}-\beta\).

Az \(\displaystyle AC\) egyenes érintője az \(\displaystyle OB\) átmérőjű félkörnek, emiatt az \(\displaystyle OCE\sphericalangle\) olyan, a félkörhöz rajzolt érintőszárú kerületi szög, amelyik az \(\displaystyle OC\) ívhez tartozik. Ehhez az ívhez tartozik a félkörben az \(\displaystyle OBC\sphericalangle=\beta\) kerületi szög, ez pedig a kerületi szögek tétele szerint azt jelenti, hogy \(\displaystyle OCE\sphericalangle=\beta\), és így \(\displaystyle COE\sphericalangle=90^{\circ}-\beta\).

Az \(\displaystyle OBC\) és \(\displaystyle ODC\) háromszögekben \(\displaystyle OB=OD=1\) az \(\displaystyle AB\) átmérőjű félkör sugara, illetve a két háromszögben közös az \(\displaystyle OC\) oldal, valamint a két-két megfelelő oldal által bezárt szögek is egyenlők, hiszen \(\displaystyle COB\sphericalangle=COD\sphericalangle=90^{\circ}-\beta\). Az \(\displaystyle OBC\) és \(\displaystyle ODC\) háromszögek tehát egybevágók, ezért a két háromszögben a harmadik oldalak is egyenlő hosszúak, vagyis \(\displaystyle BC=DC\).

Az egybevágóságból az is következik, hogy \(\displaystyle OCB\sphericalangle=OCD\sphericalangle=90^{\circ}\), azaz \(\displaystyle BCD\sphericalangle=180^{\circ}\), vagyis a \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\) pontok egy egyenesre esnek, és \(\displaystyle BC=DC\) alapján a \(\displaystyle BD\) szakasz felezőpontja valóban \(\displaystyle C\).

Statisztika:

163 dolgozat érkezett.
5 pontot kapott:	97 versenyző.
4 pontot kapott:	21 versenyző.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	6 versenyző.
Nem versenyszerű:	9 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2021. novemberi matematika feladatai