A KöMaL 2023. januári informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2023. február 15-én LEJÁRT. |
I. 580. Egy áruház a ,,minden ötödik ingyen'' mottóval árulja termékeit. Ez azt jelenti, hogy ha valaki egy vásárlás során legalább öt terméket megvesz, akkor minden ötödik termék árát elengedik. A kedvezmény számításakor a termékek sorrendjét az áruház szabja meg úgy, hogy az eladás az áruháznak a legtöbb bevételt hozza. Tehát az elengedett ötödik termékeket az áruház választja ki.
Az áruházban \(\displaystyle n\) különböző termék kapható, melyek ára \(\displaystyle a_{1}, a_{2}, \ldots, a_{n}\). Tudjuk ugyanakkor, hogy egy vevő \(\displaystyle v_{1}, v_{2},\ldots, v_{n}\) számú terméket vásárolt a bolt kínálatából. Adjuk meg ezek alapján, hogy a kedvezmények levonása után mekkora összeget kell fizetnie.
A program a standard bemenet első sorából olvassa be a termékek \(\displaystyle n\) számát (\(\displaystyle 2\le n\le 10\)), a második sorból \(\displaystyle n\) darab egész számot: a termékek egységárát (\(\displaystyle 1\le a_{i}\le 100\)), és a harmadik sorából szintén \(\displaystyle n\) egész számot: a vevő által vásárolt termékek darabszámát (\(\displaystyle 1\le v_{i}\le 100\)).
A program a standard kimenet egyetlen sorába írja a vásárlás során fizetendő összeget.
Példák:

Magyarázat: az első példában a három termékből összesen 19 darabot vásárolt a vevő, így három ötös csoport jött létre, és a kedvezmény három 24 egységárral forgalmazott termékért járt. A második példában a 20 darab termék vásárlásakor négy termék árát engedték el: három 41 és egy 70 egységárral forgalmazott termékét.
Beküldendő egy tömörített i580.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
I. 581. Bizonyára mindenki elő tud ásni valamilyen emlékfoszlányt, hogy könnyű vagy nehéz volt-e annak idején megtanulnia a szorzótáblát. Persze minden számrendszernek más a szorzótáblája. Ezek előállítása lesz a feladatunk.
Például az egyjegyű számok szorzótáblája 4-es és 8-as számrendszerben a következő:
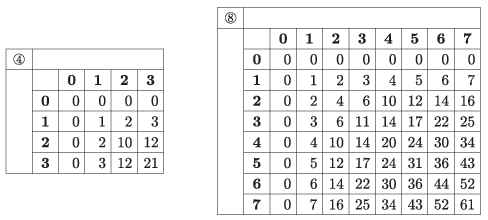
A dolgot még bonyolítja, hogy a tíznél nagyobb alapú számrendszerekben a 9 feletti számjegyeket a 36-os számrendszerig latin nagybetűkkel jelöljük: \(\displaystyle 10=\mathrm{A}\), \(\displaystyle 11=\mathrm{B}\), \(\displaystyle \ldots\), \(\displaystyle 15=\mathrm{F}\), \(\displaystyle \ldots\), \(\displaystyle 28=\mathrm{S}\), \(\displaystyle \ldots\), \(\displaystyle 34=\mathrm{Y}\), \(\displaystyle 35=\mathrm{Z}\). Természetesen például a 20-as számrendszerben a legnagyobb számjegy a 19-et jelentő J, 30-asban a 29-et jelölő T.
A feladat a következő:
1. Nyissunk meg egy üres munkafüzetet és mentsük el szorzotabla néven.
2. Csak egyetlen munkalapja legyen Tabla néven.
3. A munkalap betűtípusát állítsuk be Courier New, Nimbus Mono vagy más rögzített szélességű karakterekből álló betűtípusra.
4. Állítsuk be, hogy a munkalapon a felhasználó csak az A1-es cellába tudjon adatot írni. A lapvédelem jelszava legyen ,,komal''.
5. A munkalap szükséges celláinak szélességét állítsuk be úgy, hogy a kétkarakteres szöveg is olvasható legyen.
6. Ha az A1-es a cellába egy 2 és 36 közötti számot írunk, akkor jelenjen meg a B2-es cellától kezdődően a minta szerinti formátumban az adott számhoz mint alapszámhoz tartozó szorzótábla.
7. A munkalapot a következők szerint formázzuk:
\(\displaystyle 7.a\). Keretezés és színezés csak a szükséges cellákon legyen.
\(\displaystyle 7.b\). Az adatok cellán belüli igazítása, betűmérete és betűstílusa legyen azonos a mintán láthatóval.
Segédszámításokat az AM oszloptól jobbra vagy a 39. sor alatt végezhetünk, de ügyeljünk arra, hogy ezek a cellatartalmak alapból ne legyenek láthatók. A megoldás során saját függvény vagy makró nem használható, csak a táblázatkezelő beépített függvényei.
Minták:
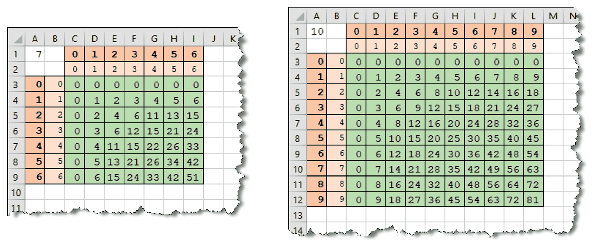
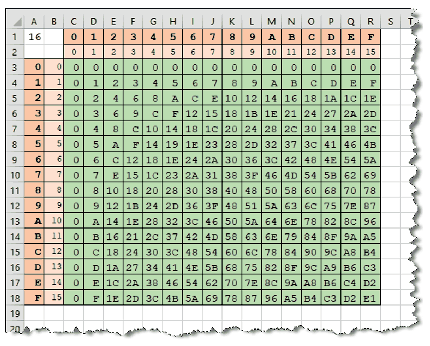
Beküldendő egy tömörített i582.zip állományban a táblázatkezelő munkafüzet, illetve egy rövid dokumentáció, amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.
(10 pont)
I. 582. (É). A magyar oktatás és nevelés történetében ritkán volt a különböző kormányokban önálló minisztériuma az oktatásnak. A rendelkezésre álló és letölthető adatbázisban az oktatásért felelős miniszterek és minisztériumok adatai állnak szerepelnek.
Az adatbázis a következő táblákat tartalmazza:
miniszter (id, mettol, meddig, nevid, miniszterium, allamforma, part)
- id a miniszteri megbízás azonosítója (szám), ez a kulcs;
mettol a miniszteri megbízás kezdő dátuma (dátum);
meddig a miniszteri megbízás befejező dátuma (dátum);
nevid a miniszter azonosítója (szám), idegen kulcs;
miniszterium a minisztérium neve, amelyhez az oktatásügy tartozik (szöveg);
allamforma a megbízás idején az államforma neve (szöveg), például: Magyar Királyság, Magyar Köztársaság stb.;
part a minisztert adó párt neve (szöveg).
szemely (id, nev)
- id a miniszteri feladattal megbízott személy azonosítója (szám), ez a kulcs;
nev a személy neve (szöveg), az adatbázisban névrokonok szerepelnek.
A táblák közötti kapcsolatok:

A következő feladatokat megoldó SQL parancsokat rögzítsük a feladatok végén zárójelben megadott névvel az om_megoldas.sql nevű állományban. A javítás során csak ennek az állománynak a tartalma lesz értékelve. Ügyeljünk arra, hogy a lekérdezésekben pontosan a kívánt mezők szerepeljenek, felesleges mezőt ne jelenítsünk meg. A feladat megoldásához a digitális kultúra emelt szintű érettségin használható XAMPP használatát javasoljuk.
1. Az oktatas.sql állomány tartalmazza az adatbázist és a táblákat létrehozó, valamint az adatokat a táblába beszúró SQL parancsokat. Futtassuk a lokális SQL szerveren az oktatas.sql parancsfájlt.
2. Adjuk meg lekérdezés segítségével, hogy 1923. január 1-én ki volt az oktatásért felelős miniszter és mi volt a minisztérium neve. (2szazeve)
3. Listázzuk lekérdezés segítségével az első 5 leghosszabb ideig miniszteri megbízású személy nevét, figyelembe véve többszöri miniszterségüket. (3top5)
4. Az egyik leghíresebb miniszter volt Klebelsberg Kuno gróf. Lekérdezéssel adjuk meg, hogy kitől vette át és kinek adta tovább a miniszteri megbízást. (4klebelsberg)
5. Adjuk meg lekérdezés segítségével, hogy Hóman Bálint első és utolsó miniszteri megbízatása között ki volt még miniszter. (5homan)
6. Lekérdezéssel határozzuk meg, hogy a magyar politikai pártok hány miniszteri megbízást kaptak. A listában a pártonkívüliek és a ki nem töltött adattal rendelkező személyek ne szerepeljenek. (6partonkent)
7. Készítsünk lekérdezést, amely kilistázza azokat a személyeket, akik több párt színeiben kerültek miniszteri pozícióba. A listában a személyek neve és a különböző pártok színeiben való megbízások száma jelenjen meg, az utóbbi szerint csökkenő sorrendben. (7tobb)
8. Adjuk meg lekérdezés segítségével azt az évet, amikortól már a ,,vallás'' szöveg nem szerepel többet a minisztérium nevében, mert önálló hivatalt kap. (8vallas)
9. Lekérdezés segítségével adjuk meg azokat a minisztériumi neveket, amelyekben nem szerepel az ,,oktatás'', ,,művelődés'' és ,,kulturális'' szavak egyike sem. A listában a minisztériumok neve ábécé sorrendben, ismétlődés nélkül jelenjen meg. (9nevek)
Beküldendő az om_megoldas.sql nevű állomány, amely a feladatok megoldását tartalmazza.
Letölhető állomány: oktatas.sql.
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2023. február 15-én LEJÁRT. |
I/S. 68. Adott egy \(\displaystyle N\)-jegyű pozitív egész szám. Egy lépés során kitörölhető egy számjegy az összes helyről, ahol előfordul, ha a visszamaradt szám pozitív szám marad, és nem kezdődik 0-val. Például egy lépés során a \(\displaystyle 33\,013\,211\) számból az 1-es számjegyek kitörlésével a \(\displaystyle 33\,032\) számot kapjuk, viszont a 3-as számjegyet nem lehet kitörölni, mert akkor a visszamaradt szám 0-val kezdődne. Hasonlóan a 777 számból sem törölhető ki a 7-es számjegy.
Adjuk meg, hogy legföljebb \(\displaystyle K\) törlés után melyik az a legkisebb szám, amit kaphatunk.
A bemenet első sorában az \(\displaystyle N\) és \(\displaystyle K\) szám szerepel szóközzel elválasztva, a második sorban az \(\displaystyle N\)-jegyű szám szerepel.
A kimenet egyetlen sorában egyetlen szám szerepeljen: a legföljebb \(\displaystyle K\) törlés után megmaradt szám.
Példák:
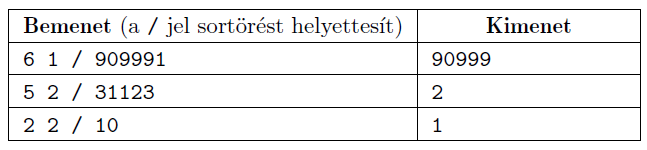
Korlátok: \(\displaystyle 1\le N, K\le 1000\). Időlimit: 0,4 mp.
Értékelés: a pontok 50%-a kapható, ha a program helyes kimenetet ad az \(\displaystyle N\le 9\) esetekben.
Beküldendő egy is68.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható. A dokumentáció tartalmazza a megoldás elméleti hátterét, az esetleg felhasznált forrásokat. Ne tartalmazzon kódrészleteket, azok magyarázata kódkommentek formájában a forrásprogramban szerepeljen.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2023. február 15-én LEJÁRT. |
S. 167. Egy hegy tetejére \(\displaystyle N\) lépcsőből álló lépcsősor vezet fel. Egy szerzetes \(\displaystyle T\) egymást követő napon felment a hegyre. Első nap az \(\displaystyle l_{1}\) lépcsőfokról indult és minden lépésnél kihagyott \(\displaystyle d_{1}\) lépcsőfokot. Rálépett tehát az \(\displaystyle l_{1}+(d_{1}+1)\), \(\displaystyle l_{1}+ {2(d_{1}+1)}\), \(\displaystyle \ldots\ \) lépcsőfokokra egészen addig, míg fel nem ért a hegycsúcsra. Ha az utolsó lépés magasabbra ért volna, mint \(\displaystyle N\), akkor rálépett az \(\displaystyle N\)-edik fokra és ezzel feljutott a hegycsúcsra.
Az első napot követő napokon az \(\displaystyle l_{i}\) és \(\displaystyle d_{i}\) értékeket a következő szabály szerint változtatta: \(\displaystyle l_{i+1} = (l_{i}+1) \mod L\) és \(\displaystyle d_{i+1} = (d_{i}+1) \mod D\), ahol \(\displaystyle 1\le i\le T-1\). Sajnos a szerzetes már nem emlékszik rá, hogy így hány lépcsőfokra lépett rá felfelé menet. Készítsünk programot, ami meghatározza ezt a számot.
A bemenet első sorában hat egész szám szerepel: a lépcsők \(\displaystyle N\) száma, a napok \(\displaystyle T\) száma, az \(\displaystyle L\) és \(\displaystyle D\) modulusok, illetve az első napon az \(\displaystyle l_{1}\) lépcsőfok, amiről indulunk, és a lépésenként kihagyott lépcsőfokok \(\displaystyle d_{1}\) száma.
A kimenet első és egyetlen sorába írjuk ki, hogy összesen hány lépcsőfokra lépett rá a szerzetes felfelé menet.
Példa:
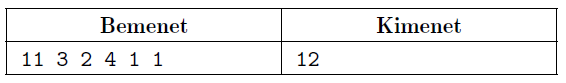
Magyarázat: az első napon az első fokról indul és minden másodikra lép rá (5 lépés). A második napon a nulladik fokról indul és minden harmadik lépcsőfokra lép rá (4 lépés). A harmadik napon az első fokról indul és minden negyedikre lép rá (3 lépés).
Korlátok: \(\displaystyle 1\le N,T \le 10^9\), \(\displaystyle 1\le L,D \le 400\), \(\displaystyle L,D\le N\), \(\displaystyle 0\le l_{1}< L\), \(\displaystyle 0\le d_1< D\). Időkorlát: 1 mp.
Értékelés: A pontok 40%-a kapható, ha a program helyes kimenetet ad a \(\displaystyle {T\le 10^5}\) bemenetekre.
Beküldendő egy s167.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható. A dokumentáció tartalmazza a megoldás elméleti hátterét, az esetleg felhasznált forrásokat. Ne tartalmazzon kódrészleteket, azok magyarázata kódkommentek formájában a forrásprogramban szerepeljen.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

