Fórum: Trigonometria

[1] [2] [3]

Szeretnél hozzászólni? Jelentkezz be.

2007-03-24 00:12:29

A lap alsó fertályán megtalálod a szinuszt is.

Előzmény: [38] csocsi, 2007-03-13 17:34:12

[38] csocsi	2007-03-13 17:34:12
Sziasztok! Nekem lenne egy trigonometriához kapcsolódó kérdésem. A kérdés a következő: hogy próbálták elnevezni a nyelvújítás során a szinuszfüggvényt? Ezt a kérdést órán kaptuk, és már égen földön kerestem, de még egy névhez sem tudtam kötni a kérdést sajnos. Remélem tudtok segíteni!

[37] HoA	2006-12-15 23:42:38
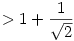
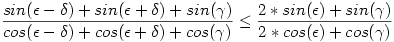
Szélsőérték számítás nélküli bizonyítás arra, hogy a kifejezés (k) értéke hegyesszögű háromszögre $> 1 + \frac1{\sqrt2}$ , derékszögűt is megengedve pedig ez a minimum. Vizsgáljuk k változását, ha a háromszög két szögét számtani közepükkel helyettesítjük. Legyen $\beta$ $\ge$ $\alpha$ , $\beta$ + $\alpha$ =2 $\epsilon$ , $\beta$ - $\alpha$ =2 $\delta$ Mikor igaz ez az egyenlőtlenség? 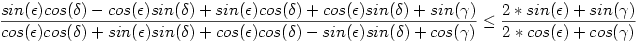$\frac{sin(\epsilon-\delta)+sin(\epsilon+\delta)+sin(\gamma)}{cos(\epsilon-\delta)+cos(\epsilon+\delta)+cos(\gamma)} \le \frac{2sin(\epsilon)+sin(\gamma)}{2cos(\epsilon)+cos(\gamma)}$ $\frac{sin(\epsilon)cos(\delta)-cos(\epsilon)sin(\delta)+sin(\epsilon)cos(\delta)+cos(\epsilon)sin(\delta)+sin(\gamma)}{cos(\epsilon)cos(\delta)+sin(\epsilon)sin(\delta)+cos(\epsilon)cos(\delta)-sin(\epsilon)sin(\delta)+cos(\gamma)} \le \frac{2sin(\epsilon)+sin(\gamma)}{2cos(\epsilon)+cos(\gamma)}$ Egyszerűsítés után a kifejezés ilyen alakú: $\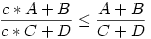frac{cA+B}{cC+D} \le \frac{A+B}{C+D}$ , ahol c=cos( $\delta$ ),A=2*sin( $\epsilon$ ),B=sin( $\gamma$ ),C=2*cos( $\epsilon$ ),D=cos( $\gamma$ ) Átrendezve cAC +BC + cAD + BD <= cAC + cBC + AD + BD BC + cAD <= cBC + AD (1-c)(AD-BC) >= 0 Mivel c egy hegyesszög cosinusa, 0 < c < 1, az egyenlőtlenség AD - BC előjelétől függ. 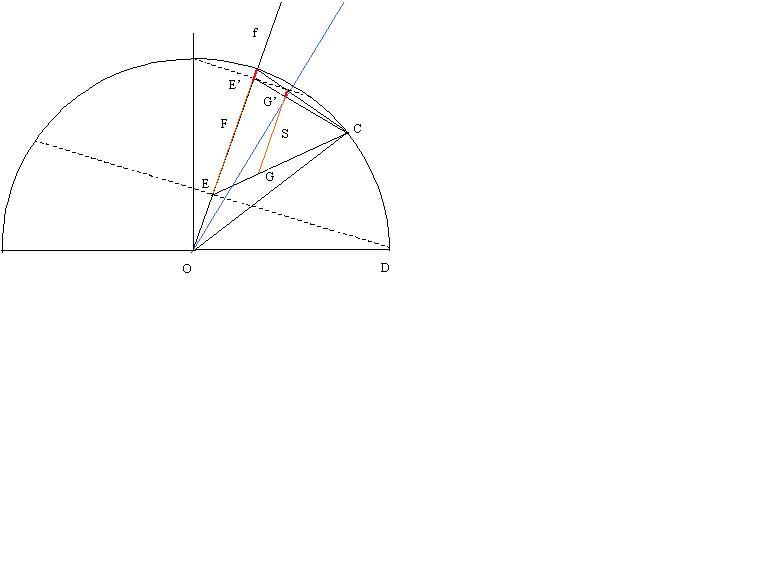AD-BC=2sin( $\epsilon$ )cos( $\gamma$ )-2*cos( $\epsilon$ )sin( $\gamma$ )=2*sin( $\epsilon$ - $\gamma$ ) Hegyesszögekről lévén szó egyenlőtlenségünk irányát $\epsilon$ és $\gamma$ nagyságviszonya szabja meg. Ha gamma a legnagyobb szög, alfát és bétát átlagukkal helyettesítve a k kifejezés csökken. Ezt az esetet illusztrálja Bohner Géza ábrája: Az OS egyenes meredeksége akkor a legkisebb, ha F E-től legtávolabbi és így S G-től legtávolabbi helyzetébe kerül, vagyis mikor alfa = beta . Ha gamma a legkisebb szög, alfát és bétát átlagukkal helyettesítve a k kifejezés nő, alfa és béta különbségét növelve k csökken. Ezt mutatja az itteni ábra. Ha háromszögünk legfeljebb derékszögű lehet, F az egységkörtől nem juthat E-ig csak E'-ig, így S is csak G'-ig juthat G helyett. K legkisebb értékét az OG' egyenes meredeksége adja. Legyen egy tetszőleges H₀ hegyesszögű háromszögre k értéke k₀ . Legyen $\gamma$ $\le$ $\beta$ $\le$ $\alpha$ . Ekkor $\gamma$ -t rögzítve $\alpha$ -t 90^o-ra növelve az új H₁ háromszögre k=k₁<k₀ . Betűzzük át H₁ szögeit, úgy hogy $\alpha$ $\le$ $\beta$ < $\gamma$ =90^o legyen. 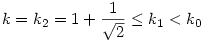Most $\gamma$ -t rögzítve (90^o ) $\alpha$ = $\beta$ =45^o adja a legkisebb k értéket jelentő H₂ háromszöget, melyre $k = k_2 = 1 + \frac1{\sqrt2} \le k_1 < k_0$ . Mivel H₀ tetszőleges hegyesszögű háromszög volt, a bizonyítást befejeztük.

Előzmény: [32] Ali, 2006-10-05 14:16:48

[36] S.Ákos	2006-10-18 19:55:07
Köszi
Előzmény: [35] jonas, 2006-10-17 19:00:05

[35] jonas	2006-10-17 19:00:05
Ha ilyesmit keresel, nekem a Csebisev polinomok az egyik kedvenc témám. Magyarul a Pólya György--Szegő Gábor feladatgyüjteményben olvashatsz róluk bővebben.
Előzmény: [34] S.Ákos, 2006-10-17 18:52:22

[34] S.Ákos

2006-10-17 18:52:22

szerintem eléggé lejártaom magam ezzel, de én még nem találkoztam olyan képlettel, amely megadta volna

sin $\lambda$ $\alpha$ ,cos $\lambda$ $\alpha$ ,tg $\lambda$ $\alpha$ ,ctg $\lambda$ $\alpha$ értékét. $\lambda$ -n egy adott konstanst értek

[33] BohnerGéza	2006-10-05 18:59:05
Az Euklides-szel való játszadozás alapján biztosra vehető, máshogy még nem néztem.
Előzmény: [32] Ali, 2006-10-05 14:16:48

[32] Ali	2006-10-05 14:16:48
És az igaz-e, hogy hegyesszőgű háromszögre a kérdéses kifejezés értéke nagyobb, mint $1+1/\sqrt2$ ?
Előzmény: [31] BohnerGéza, 2006-10-05 09:13:31

[31] BohnerGéza	2006-10-05 09:13:31
A 6. hozzászolás feladatának megoldása: . .

Előzmény: [6] epsilon, 2006-09-22 05:54:52

[30] epsilon	2006-10-01 13:23:36
Hát igen, újra átolvasva a megoldásodat, az ottani jelölésrendszerrel is már látszott, és nem vettem észre :-( Kösz az ismételt magyarázatot!

[29] nadorp	2006-10-01 08:32:50
Az az állítás, hogy a tört értéke 1 , EKVIVALENS az általad is kihozott egyenlőséggel. Tehát HA $\alpha$ kisebb a felső korlátnál, akkor létezik hozzá pontosan egy jó $\beta$ . Határesetben $\alpha$ =0, $\beta$ =30^o, $\gamma$ =150^o
Előzmény: [28] epsilon, 2006-10-01 07:01:18

[28] epsilon	2006-10-01 07:01:18
Köszi nadrop! Én csak idáig jutottam el:(az ábra az alján van) Az egyenlőtlenségből valóban megközelíthető az alfa értéke, de azt nem látom tisztán, hogy valóban FENNÁLHAT-e a tört 1-gyel való egyenlőtlensége, mert én arra következtetek, HA fennálna, akkor az alfa értéke megközelítőlegannyi lenne mint amennyit Te írtál!

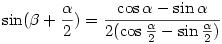[27] nadorp

2006-09-30 21:48:54

Vázolok egy levezetést, bocs ha egy kicsit unalmas.

Feltehető, hogy $\alpha$ $\leq$ $\beta$ $\leq$ $\gamma$ .

sin ( $\alpha$ -45^o)+sin ( $\beta$ -45^o)+sin ( $\gamma$ -45^o)=0, ezért az egyik tag negatív,azaz $\alpha$ <45^o ( egyenlőség nem lehet,mint láttuk)

sin $\alpha$ +sin $\beta$ +sin ( $\alpha$ + $\beta$ )=cos $\alpha$ +cos $\beta$ -cos ( $\alpha$ + $\beta$ )

sin $\beta$ (1+cos $\alpha$ -sin $\alpha$ )+cos $\beta$ (-1+cos $\alpha$ +sin $\alpha$ )=cos $\alpha$ -sin $\alpha$

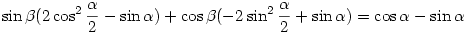
$\sin\beta(2\cos^2\frac\alpha2-\sin\alpha)+\cos\beta(-2\sin^2\frac\alpha2+\sin\alpha)=\cos\alpha-\sin\alpha$

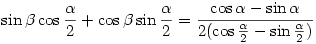
$\sin\beta\cos\frac\alpha2+\cos\beta\sin\frac\alpha2=\frac{\cos\alpha-\sin\alpha}{2(\cos\frac\alpha2-\sin\frac\alpha2)}$

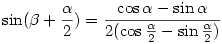
$\sin(\beta+\frac\alpha2)=\frac{\cos\alpha-\sin\alpha}{2(\cos\frac\alpha2-\sin\frac\alpha2)}$

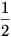A jobb oldal $\alpha$ <45^o miatt kisebb $\frac12$ -nél és pozitív, azaz a jobb oldal sin $\phi$ alkalmas hegyes szöggel.

Innen 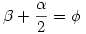$\beta+\frac\alpha2=\phi$ , hiszen a szögek nagyságára tett feltevés szerint a bal oldalon is csak hegyes szög sinusa lehet.

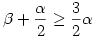$\beta+\frac\alpha2\geq\frac32\alpha$ miatt,

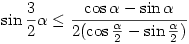
$\sin\frac32\alpha\leq\frac{\cos\alpha-\sin\alpha}{2(\cos\frac\alpha2-\sin\frac\alpha2)}$

Ezt nem részletezve ( negyedfokú egyenletlőtlenség cos $\alpha$ -ra ) azt kapjuk, hogy közelítőleg

0< $\alpha$ $\leq$ 15,876^o.

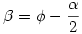
Minden egyes ilyen $\alpha$ -ra kapunk egy $\phi$ -t, és $\beta=\phi-\frac\alpha2$

Előzmény: [26] epsilon, 2006-09-30 12:59:53

[26] epsilon	2006-09-30 12:59:53
Kösz, hát úgy látszik, hiába vergődöm, hogy egy olyan konkrét esetet találjak, amikor a tört 1-gyel egyenlő :-(

[25] Sirpi	2006-09-30 12:15:56
Nem néztem át alaposan, de egy lépés biztos hibás: $\tan \alpha = 1 - \sqrt 2$ -ből $\alpha$ =-22,5^o+k^.180^o, ami nem lehet egy háromszög szöge.
Előzmény: [24] epsilon, 2006-09-30 10:54:43

[24] epsilon

2006-09-30 10:54:43

Helló Nadorp! Úgy látszik, mintha igazad lenne, de akkor hol a hibí a következőkben ? :-( Átjelölöm: alfa=A, beta=B, gamma=C. (sajnos a LaTex-ben nem vagyok jártas,a MatghTypet használom Wordben) :-(

Legyen C=45°ekkor A+B=135° Az 1-gyel való egyenlőség így alakul: sinA+sinB=cosA+cosB és most beírom a B=135°és elvégzem a sin és cos képltekkel a különbségek kifejtését, és ez marad sinA=(1-gyök2)cosA innen tgA= 1-gyök2 ahogy néztem a táblázatban ez megközelítőleg 67°és a B=135°- A. Hol a hiba? :-(

Előzmény: [22] Lóczi Lajos, 2006-09-28 19:12:32

[23] nadorp

2006-09-29 09:01:39

Sőt,ha valamelyik szög 45^o, akkor a tört értéke sosem lesz 1. Ui. legyen pld. $\gamma$ =45^o. Ekkor

sin $\alpha$ +sin $\beta$ +sin $\gamma$ =cos $\alpha$ +cos $\beta$ +cos $\gamma$ miatt

sin ( $\alpha$ -45^o)+sin( $\beta$ -45^o)=0

$2\sin(\frac{\alpha+\beta}2-45^\circ)\cos\frac{\alpha-\beta}2=0$

Ebből $\alpha$ + $\beta$ =90^o+k^.360^o vagy $\alpha$ - $\beta$ =180^o+k^.360^o következik, de ekkor $\alpha$ , $\beta$ , $\gamma$ nem egy háromszög szögei

Előzmény: [22] Lóczi Lajos, 2006-09-28 19:12:32

[22] Lóczi Lajos	2006-09-28 19:12:32
A [17]-es hozzászólásomban szereplő példa cáfolja ezt az állítást.
Előzmény: [21] epsilon, 2006-09-28 11:50:05

[21] epsilon	2006-09-28 11:50:05
Na végre sikerült, elemi trigóképletekkel könnyen belátható, hogy a tört értéke pontosan akkor 1 ha valamelyik szög mértéke 45°, és a másik kettő összege 135°, és ezen belül tetszőlegesek lehetnek. Tehát végtelen sok esetben 1 a tört értéke! De csakis a fenti esetekben!
Előzmény: [16] Lóczi Lajos, 2006-09-24 21:05:09

[20] epsilon	2006-09-25 21:09:07
Gratulálok nadrop! Szép elegán bizonyítás!

[19] nadorp

2006-09-25 11:15:02

Egy kis hiánypótlás az előzőekhez. A végén felhasználtam, hogy a sinusok együtthatói nemnegatívok. Ha például $\gamma$ tompaszög, akkor

cos $\alpha$ +cos $\gamma$ =cos $\alpha$ -cos ( $\pi$ - $\gamma$ ) $\ge$ 0, hiszen

$\alpha$ $\leq$ $\pi$ - $\gamma$ és a cosinus függvény hegyesszögekre csökken.

Előzmény: [18] nadorp, 2006-09-25 10:48:45

[18] nadorp

2006-09-25 10:48:45

Sziasztok!

Az alsó korlát nyilván 0, hiszen ha pld. $\alpha$ = $\beta$ elég kicsi, ekkor $\gamma$ elég nagy , így a tört számlálója közel van nullához, a nevezője pedig egyhez. Nézzük a felső korlátot!

(sin $\alpha$ +sin $\beta$ +sin $\gamma$ )(cos $\alpha$ +cos $\beta$ +cos $\gamma$ )=sin $\alpha$ cos $\alpha$ +sin $\beta$ cos $\beta$ +sin $\gamma$ cos $\gamma$ +sin $\alpha$ +sin $\beta$ +sin $\gamma$

$\frac{\sin\alpha+\sin\beta+\sin\gamma}{\cos\alpha+\cos\beta+\cos\gamma}=\sin\alpha+\sin\beta+\sin\gamma-\frac{\sin\alpha\cos\alpha+\sin\beta\cos\beta+\sin\gamma\cos\gamma}{\cos\alpha+\cos\beta+\cos\gamma}$

$\frac{\sin\alpha+\sin\beta+\sin\gamma}{\cos\alpha+\cos\beta+\cos\gamma}=\frac{\cos\beta+\cos\gamma}{\cos\alpha+\cos\beta+\cos\gamma}\sin\alpha+\frac{\cos\alpha+\cos\gamma}{\cos\alpha+\cos\beta+\cos\gamma}\sin\beta+\frac{\cos\alpha+\cos\beta}{\cos\alpha+\cos\beta+\cos\gamma}\sin\gamma$

$\frac{\sin\alpha+\sin\beta+\sin\gamma}{\cos\alpha+\cos\beta+\cos\gamma}<\frac{\cos\beta+\cos\gamma}{\cos\alpha+\cos\beta+\cos\gamma}+\frac{\cos\alpha+\cos\gamma}{\cos\alpha+\cos\beta+\cos\gamma}+\frac{\cos\alpha+\cos\beta}{\cos\alpha+\cos\beta+\cos\gamma}=2$

Egyenlőség nyilván nem lehet, de ha pld $\alpha$ = $\beta$ elég közel van a 90^o-hoz, akkor a közelítés tetszőlegesen jó lehet.

Előzmény: [6] epsilon, 2006-09-22 05:54:52

[17] Lóczi Lajos	2006-09-24 23:07:09
Bocsánat, az előbb nem figyeltem, hogy a numerikus értékek nem lehetnek egy háromszög szögei, de pl. $\alpha$ =0.1 és $\beta$ $\approx$ 0.441278 már jó, itt az eredeti tört kb. 1.
Előzmény: [15] Lóczi Lajos, 2006-09-24 20:47:43

[16] Lóczi Lajos

2006-09-24 21:05:09

Nyilvánvaló módon nem látom, hogy ha $\alpha$ és $\beta$ egy háromszög szögei, akkor

cos ( $\alpha$ )+cos ( $\beta$ )+cos ( $\pi$ - $\alpha$ - $\beta$ ) $\ne$ 0.

(Persze egy újabb, az előzőekkel teljesen analóg szélsőértékvizsgálattal hamar kijön.)

Előzmény: [15] Lóczi Lajos, 2006-09-24 20:47:43

[15] Lóczi Lajos	2006-09-24 20:47:43
Például $\alpha$ =1, $\beta$ $\approx$ 3.029447-nél a tört kb. 1. Ilyen hely létezése a függvény folytonosságából következik. (A leírt bizonyításhoz hozzá kellett volna tennem, hogy a vizsgált kétváltozós függvény mindenhol folytonos (sőt, deriválható) a megadott paramétertartományon. Általában viszont a nevező lehet 0 is!)
Előzmény: [14] epsilon, 2006-09-24 20:21:53

[1] [2] [3]

Már regisztráltál?
Új vendég vagy?