| [96] marcius8 | 2018-06-26 13:05:09 |
 Ha még aktuális a szabályos 11szög szerkesztése, akkor a következő képleteket szerkesztettem. A képletek alapján ki lehet találni, hogy hogyan lehet szabályos 11szöget szerkeszteni csak körző és egyélű beosztás nélküli vonalzót használva véges sok lépésben, feltéve ha valahogy tudunk szöget öt egyforma nagyságú részre osztani.
|
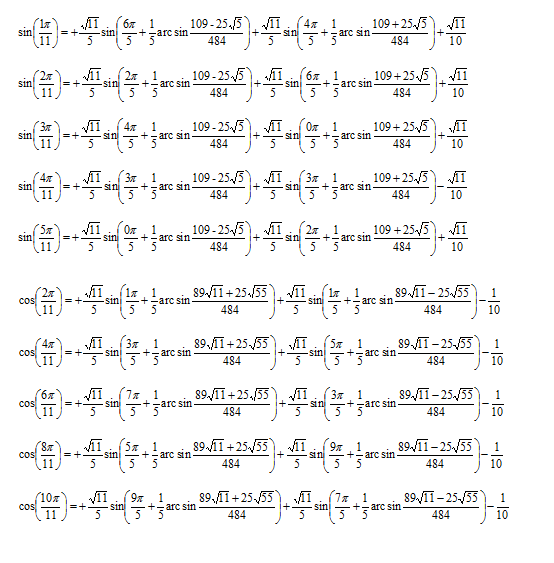 |
|
|
| [94] SmallPotato | 2009-10-04 18:32:07 |
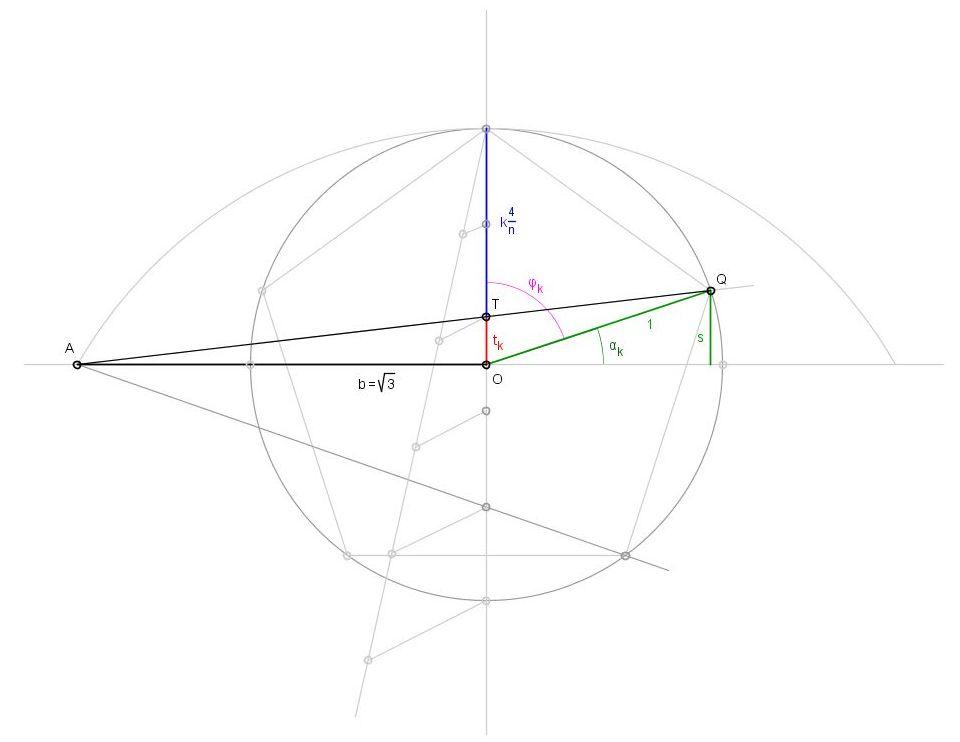
 Készítettem egy ábrát is. Legyen a kör sugara egységnyi. A  k szög a k-adik csúcshoz tartozó szög a pozitív függőlegestől jobbra mérve. Ennek kiszámításához először a tk szakaszt állapítjuk meg; ez ugye k szög a k-adik csúcshoz tartozó szög a pozitív függőlegestől jobbra mérve. Ennek kiszámításához először a tk szakaszt állapítjuk meg; ez ugye
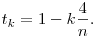
Az 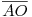 szakasz a szerkesztésből adódóan szakasz a szerkesztésből adódóan  ; ezzel az ; ezzel az 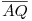 egyenes egyenlete egyenes egyenlete
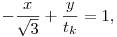
másfelől
x2+y2=1,
amelyekből az y (=s) értékére
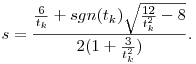
A másodfokú egyenlet két gyöke közül nekünk mindig a nagyobb abszolút értékű kell; ezért szerepel a sgn(tk) szorzó.
Az ábrából láthatóan a kapott s érték az  k szög szinusza, így abból k szög szinusza, így abból  k, majd k, majd
 k=90°- k=90°- k k
révén a  k is számítható. (s és így k is számítható. (s és így  k is természetesen előjeles mennyiség; ennek megfelelően k is természetesen előjeles mennyiség; ennek megfelelően  k elvi maximuma 180°). k elvi maximuma 180°).
|
 |
| Előzmény: [93] SmallPotato, 2009-10-04 12:57:43 |
|
| [93] SmallPotato | 2009-10-04 12:57:43 |
 Számolgattam egy kicsit. (Pontosabban ax Excelt kértem meg erre.)
n=10001-ig az előforduló legnagyobb abszolút szöghiba (a  szög tekintetében) 0,637°. Ez a fajta hiba minden n esetén a felfelé mutató függőlegestől számított első csúcsnál a legnagyobb, és a jelzett értéket a 21- ill 23-szögnél éri el. szög tekintetében) 0,637°. Ez a fajta hiba minden n esetén a felfelé mutató függőlegestől számított első csúcsnál a legnagyobb, és a jelzett értéket a 21- ill 23-szögnél éri el.
Ugyanerre a csúcsra a relatív szöghiba az n növekedésével gyakorlatilag folyamatosan, bár degresszíven nő; pl. 9-szögnél 0,7 százalék, 25-szögnél 4,4 százalék, 10001-szögnél 10,2 százalék.
Ha a szöghibát a vízszintes átmérő végpontjához legközelebbi csúcsnál (a függőlegestől addig halmozott középponti szögek összegére nézve) tekintjük, akkor a hiba legnagyobb abszolút értéke (ez n=5 esetén áll elő) nincs 0,05° sem, és n növekedésével csökken, nagy n-ek esetében gyakorlatilag n-nel fordítottan arányos. Pl. n=1001 esetén a hiba 3,8.10-4 fok, n=10001 esetén 3,8.10-5 fok.
E szög relatív hibája pedig szintén n=5 esetén a legnagyobb (0,07 százalék) és n növekedésével szintén csökken, az előbbiekből adódóan nagy n-ek esetén szintén körülbelül n-nel fordított arányban; pl. n=1001 esetén a relatív hiba 4,2.10-4 százalék, n=10001 esetén 4,2.10-5 százalék.
|
| Előzmény: [88] Stewe, 2009-09-30 12:31:18 |
|
| [92] SmallPotato | 2009-10-04 12:04:01 |
 Én is annyinak számolom ... de a szövegben n-szöget ír. Az ábra is csak egy példa az n-szög szerkesztésére, ahol n-re csak annyi "követelményt" szoktunk tenni, hogy prím, esetleg csak hogy páratlan legyen. (Páros n-re is működik, de olyat az n/2 esetből szögfelezéssel biztosan lehet szerkeszteni.) Emellett a topikcím pl 11-szögről szól.
|
| Előzmény: [91] SAMBUCA, 2009-10-03 21:49:47 |
|
|
| [90] SmallPotato | 2009-09-30 14:54:49 |
 "Szabályos n oldalú sokszög szerkesztése szakközépiskolai tananyag, holott a matematika ezt nem teszi lehetővé."
A teáltalad említett tananyag módszere (és a mellékelt ábrán végrehajtott műveletsor) általános esetben nem vezet szabályos sokszöghöz. Pontatlan (azaz közelítő) szerkesztést a matematika is megenged, csak akkor az eredményt nem nevezhetjük szabályos sokszögnek.
A mellékelt módszer pontossága pedig függ az n-szög oldalszámától. Melyik esetre volnál kíváncsi?
|
| Előzmény: [88] Stewe, 2009-09-30 12:31:18 |
|
| [89] Stewe | 2009-09-30 12:33:29 |
 pi=22/7... Ez biztos? :)))
|
|
| [88] Stewe | 2009-09-30 12:31:18 |
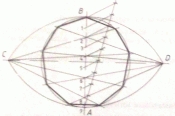
 Szabályos n oldalú sokszög szerkesztése szakközépiskolai tananyag, holott a matematika ezt nem teszi lehetővé. Meg tudja mondani valaki, hogy a képen szereplő módszer mennyire pontatlan? Jobb kép sajnos nem fér el.
|
 |
|
|
| [86] SAMBUCA | 2009-02-01 09:12:41 |
 Sziasztok,
persze, csak poén volt, ha nem tűnt volna fel :)) meghagyom másnak a dicsőséget azt hiszem :)
üdv,
Egri Attila (2004 HUN1 :P)
|
|
| [85] HoA | 2009-01-29 12:56:38 |
 Tetszik szellemes megoldásod! De azt hiszem, nem jó helyen viccelődsz. Félek, azoknak, akiknek nem világos, hogy ezen a fórumon a szerkesztéseket, egyéb kikötések híján, "Euklídeszi sík, körző+vonalzó" peremfeltételekkel értjük, nem megy át a humor.
|
| Előzmény: [83] jonas, 2009-01-28 12:54:58 |
|
|
| [83] jonas | 2009-01-28 12:54:58 |
 Tizenegyszöget tényleg nem nehéz: kihasználva, hogy  =22/7, egyszerűen fogsz egy 7 egység sugarú kört, és fölmérsz a kerületén egy 4 egység hosszú ívet (nem húrt), és ez megadja a tizenegyszög két csúcsát. =22/7, egyszerűen fogsz egy 7 egység sugarú kört, és fölmérsz a kerületén egy 4 egység hosszú ívet (nem húrt), és ez megadja a tizenegyszög két csúcsát.
|
| Előzmény: [81] SAMBUCA, 2009-01-28 02:18:11 |
|
| [82] Sirpi | 2009-01-28 11:56:32 |
 Na, akkor most már csak a peremfeltételeket kell tisztáznunk... Euklídeszi sík, körző+vonalzó? Vagy mi egyebet használsz hozzá? Mert pl. egy madzaggal meg két rajzszöggel tetszőleges ellipszist is lehet szerkeszteni (tudom, most nem azt kell, csak egy példa volt).
|
| Előzmény: [81] SAMBUCA, 2009-01-28 02:18:11 |
|
| [81] SAMBUCA | 2009-01-28 02:18:11 |
 Sziasztok,
most bukkantam rá (újra) erre a topikra :) Hogy hogyan??? Elég volt rákeresni "szabályos 17-szög" képekre googliban, és első helyen adta Maga Petit :D
Látom lecsillapodtak már a kedélyek, megjegyezném hogy azt hiszem én meg tudom szerkeszteni a szabályos 11-szöget, Galois-elmélet ide vagy oda (még jó, hogy nem azt kaptam anno algebravizsgán) :)))
Sambuca
|
|
|
| [79] mediator | 2007-07-14 09:22:06 |
 Folytatás Kertitörpének, második rész:
Ez a közbeszúrt megjegyzés senkit se zavarjon meg, csupán érdekességként említettem meg. Ez az úgynevezett Barcaság, - amit II. András a Lovagrendnek adományozott, egy igen érdekes terület. Egy szabályos medence, és ha felállunk a földvári várrom falára, akkor a teljes medencében körbe láthatunk. Látjuk azt az öt várat, amelyet a Lovagrend építhetett.
Földvár régi neve Marienburg volt. A Lovagrend védőszentje volt Mária, és Róla kapta a nevét. Erről, és még nagyon sok egyéb történelmi tényről hatalmas mennyiségű írásos anyagot lehet találni németországi levéltá-rakban, és természetesen a neten is. Itt említem meg, hogy a falu templomának oltára mögötti falon még a múlt század végén is látható volt egy freskó, amely Mária előtt térdelő lovagokat ábrázolt, de sajnos azóta ezt a képet gondosan fehérre meszelték.
Térjünk vissza az ábrához. Tehát adva van egy szabályos kör, Teliu-val a középpontban. Ennek a körnek a sugara a Teliu Codlea távolság. Teliu-val kapcsolatosan még lenne egy apró érdekesség. Ha egy egyenessel összekötjük az egymástól több tíz kilométer távolságra lévő két hegycsúcsot, - Pásztor csúcs és a Lakóca csúcs akkor ez az egyenes metszi a Teliu felett lévő várrom, és a brassói öregvár ikonját. Véletlen lehet, de azért érdekes. A debreceni egyetem professzora Pósán László, aki avatott szaktekintélye ennek a témának, még könyve is megjelent néhány évvel ezelőtt, és Ő is érdekesnek itélte meg ezt a feltevést, és azt kérte, hogy próbáljak meg más helyszíneken is geometriai alakzatokat keresni a térképen. Értsd: olyan területeken, ahol a lovagrendek ( Teutonok, Keresztesek ) várakat építettek. Sajnos nem kaptam meg Tőle a megígért térképeket, és mint mondtam, belefáradtam a témába, így nem tudtam még magamnak se igazolni az elképzeléseim helyességét.
Az mindenesetre az igen érdekes, hogy bizonyos logika szerint helyezkednek el ezek a várak a térben, és egymáshoz képest is. Nem szeretném a gondolatmenetet, és a fórum tagjait megzavarni, de ha már a fenti néhány sort leírtam, kénytelen vagyok néhány újabb érdekességet megemlíteni. Kertitörpe többek között ezt írja: Előfordulhat, hogy nem is 11szög-alakban helyezkednek el a várak, hanem más síkidomban.
Igaza van. Pontosan ez az a körülmény, ami engem is összezavart, elbizonytalanított. Ezen a területen (Barcaság) és ezen a térképen a várakkal kapcsolatosan több hasonló geometriai alakzatot tudok megrajzolni, de nem látom közöttük az összefüggéseket. Feltételeztem, hogy valaki, valamit üzent az utókornak, de nem tudom, hogy ki üzent, miért, és mit. Lassan már én is elhiszem magamról, hogy tényleg bolond vagyok.
Mindenesetre az igen érdekes a számomra, hogy egy egyenessel össze lehet kötni Jeruzsálemet a dán szigettel Bornholm-mal, amit mások is megtettek már, de ők sem tudják, hogy ez a valóságban több ezer kilométeres képzeletbeli vonal egyetlen olyan települést érint Európában, ahol lovagrendi vár van. Ez a vár pedig éppen Feketehalom-Codlea, ami az egyik általam szerkesztett geometriai alakzatban egy Dávid csillag egyik szárán van, ami 30 fokos szöget zár be Földvár várával. ( Ez aztán igazán bonyolultra sikeredett, de ez akkor is így van, és én látom az ábrát, amit kérésre szívesen elküldök bárkinek. )
Térjünk vissza a 11 szög problémájához. Tehát adva van a középpont ( Teliu ). Felvesszük a körzőnkkel a képzeletbeli kör sugarának hosszát ( a Teliu azaz Codlea távolság ), és megrajzoljuk a kört. Ez a körív metszi Höltövény várát. A következő lépés a szerkesztésben ha ez szerkesztésnek számit, hogy a Codlea Höltövény távolságot, ami a köríven adódik rámérjük a körívre, és ezzel a kört 11 egyenlő cikkre osztottuk fel. Ennyi csak a varázslat. Hogy ez miért van így, nem tudom. Hogy mi köze van ennek a matematikához, azt sem tudom, de remélem, hogy ez NEM VÉLETLEN, és bízom abban, valaki egyszer megfejti ezt a titkot.
Az általam rajzolt ábrát megpróbálom feltenni a szöveg mellé, de ha nem sikerül, akkor kérésre bárkinek szívesen elküldöm e-mail-ben.
Még egy megjegyzés a korábbi hozzászólásokhoz. Én a dolgokat csak a logika felöl tudom megközelíteni, mert a matematika nem az én világom. Az általam korábban felvetett gondolat, miszerint a régi öregek valami miatt a kört nem 360 fokra, hanem 440 fokra osztották, lehet, hogy nagyon rossz gondolat, de az bizonyosnak látszik, hogy ha a lányom születésnapjára nem 359 vendég jön, hanem 439, akkor is adnom kellene minden gyereknek ugyanakkora tortaszeletet. Lehet, hogy ebben is tévedek?
|
| Előzmény: [76] kertitörpe, 2007-05-11 22:59:32 |
|
| [78] mediator | 2007-07-14 09:16:44 |
 Ha valaki még van ezen a fórumon, akkor elmondom a gondolataimat, amelyek eszembe jutottak akkor, amikor Kertitörpe hozzászólását újra, és újra elolvastam.
Ő ezt írja többek között: A tizenegy szög keresése közben a pontatlanságokat kell figyelni. Először rajzoljuk fel a síktérképre a tizenegy szöget (elhanyagoljuk a Föld felülete és a sík közötti egyenlőtlenségeket); ha a csúcsokban nem találunk semmit, kezdjünk köröket rajzolni a feltételezett helyek köré, amíg nem ér el a peremük a várak feltételezhető helyéig. Ez csak egy módszer, várom a jobb ötleteket. Jó ötleteket vár. Ezen a ponton jöttem rá, hogy én korábban vagy nem jól írtam le a gondolataimat, vagy a vitapartnerek nem jól értették. Leírom azt, hogy én mit állítottam.
Első lépésként meghatároztam a kiindulási pontot. Abból indultam, ki, hogy az nem lehet véletlen, ha egy egyenesen, amit két hegycsúcs között húztam meg, két várrom is van, amelyekről több kutató is azt állítja, hogy azokat a Német Lovagrend építette. ( A geometriai ábrák rajzoláshoz a Freeytag féle Románia térképet használtam. )
Mondjuk azt, hogy ez a pont a térképen Teliu ( A mostani magyar neve a falunak Keresztvár. Van a falu felett két várrom, de a történészek egy része vitatja, hogy ezeket a várakat a Keresztes Lovagok építették volna, és ebbe a vitába most mi ne bonyolódjunk bele. Fogadjuk el kiindulási pontnak ezt a helyet. )
A második pont CODLEA falu legyen. A falu magyar neve Feketehalom, és itt is áll egy várrom a falu felett, de erről a várról tudják (?) hogy a Lovagrend építette. Ennek a várnak egyébként az én elképzeléseim szerint igen fontos szerepe van. Itt említem meg, hogy ezen a térképen jelölve vannak a várromok is, és én a körzőmet mindig ezeknek a kis ábráknak a közepébe szúrom bele. Ezek a kis ábrák adják azokat a pontokat, amelyek a viszonylagos pontosságát biztosítják az ábrának, de csak ezzel a Freeytag féle térképpel tudtam a magam ábráját ilyen módon megrajzolni. Vagy ez a térkép igazán valóság hű, vagy egy fatális véletlennel állunk szemben.
A körzőm hegyét beleszúrtam a Teliu felett lévő várrom ikonjába, és kinyitottam a körzőmet, annyira, hogy a grafit a Codlea felett lévő ikon közepén legyen. Ezzel a körzőnyílással rajzoltam egy körívet a térképre. Ez a körív pontosan metszette a térképen lévő következő várrom ikonját. Ez a várrom Höltövény vára. Ennek a várnak az építését sem vitatják el a Lovagrendtől, és látótávolságra van Codlea-tól, Brassó várától, valamint Földvártól, a mai nevén Feldiora-tól, ami tudottan a Német Lovagrend központja volt.
|
| Előzmény: [76] kertitörpe, 2007-05-11 22:59:32 |
|
| [77] mediator | 2007-07-10 13:54:57 |
 Üdvozletem a Fórum látogatóinak. Annak idején kaptam annyi hideget-meleget, hogy elment a kedvem attól, hogy matematikai tudás nélkül vitatkozzak a matek zsenikkel. Védeni egy "igazságot", amit még bizonyitani sem tudok, oktalanság. Most, hogy sok hónappal később, - szinte véletlenül megnéztem az oldalt, - kénytelen vagyok újra szólni. Különösen Neked, a dicséretért. Az sem érdektelen, hogy valamit elinditottam, és az a "valami" elkezdett saját életet élni.
A várakról, és erről az egész őrült teoriáról még sokat tudnék mondani, de tényleg csak akkor lenne érdemes ezt megtennem, ha nem a matematikai tétel megdöntésének szándékával tenném. Ezt pedig, mint korábban irtátok, nem egy matek topikon kellene tennem.
Tényleg jó érzés volt visszajönni közétek, és ha kell a "történelmi" vonatkozású információ valakinek, irthat nekem. A mediator@primposta.com cimre is.
|
| Előzmény: [76] kertitörpe, 2007-05-11 22:59:32 |
|
| [76] kertitörpe | 2007-05-11 22:59:32 |
 Először is gratulálni szeretnék mediatornak a felfedezéséért; kitartást neki, de legfőképp egészséget!
Apámtól örököltem a történelmi rejtélyek iránti érdeklődésem, rendkívül izgalmas dolognak tartom ezt a témát. A problémához sok segítséget nyújthatnak a műholdfelvételek, mindenkinek ajánlom a google earth ingyenes verzóját, melyet innen tölthet le(jobb felső, zöld gomb): http://earth.google.com/
Én még csak egy matek szakos gimnazista vagyok, bármilyen tévedésemet javítsátok ki, bélyegezzetek naivnak, ha kell.
Szerintem a megszerkeszthetőségen nem érdemes vitatkozni; meglehetősen kicsi az esélye, hogy szinte minden matematikus tévedett volna, nem beszélve arról, hogy ellenkező eseben megdőlne az egyik alapvető axióma, amely a jelen matematikát alkotja: egy állításnak és komplementerének nincs metszete, hiszen maga a komplementer definíciója biztosítja ezt (egy állítás és komplementerének teljes eseményrendszert alkot) (6. hozzászólás 1. mondata,[Sirpi]) Ha ez az axióma megdőlne, egy új, más matematikát kellene bevezetni(pl. az euklideszi geometria után a nemeuklideszi), bár ilyen önmagának ellentmondó rendszerben nem lehetne bármit is bizonyítani(!). Ezt axiómák nélküli matematikát(!!!) szerintem nem lehetne sokmindenre használni(várom az ellenvéleményeket; remélem, lesznek).
Szerencsére a problémánk egyszerűbb. Egy (majdnem)szabályos 11szöget keresünk. Itt inkább a fizikus gonbdolkodásmódot kövessük: bizonyos dolgokat elhanyagolunk, bizonyosakat megtartunk. A feltételezések kötetekre rúghatnának, hogy hányféle eljárással tudtak a középkori mérnökök közelítőleg 11szöget alkotni. Az sem biztos, hogy sikerült nekik, de a térképről leolvasva van esélye, tehát tételezzük fel: igen. Mivel várakról van szó, relatíve nagy építményekről, adjuk meg, mik lehetnek a maximális hibakorlátok, amik nem befolyásolják túlzottan az ábrát. Hibaforrások:- a Föld közelítőleg forgási ellipszoid - a felülete szabálytalan - a műszerek pontatlanok voltak - természeti akadályok a meghatározott csúcsokban; így nem épülhetett oda vár - stb.
A tizenegyszög keresése közben a pontatlanságokat kell figyelni. Először rajzoljuk fel a síktérképre a tizenegyszöget(elhanyagoljuk a Föld felülete és a sík közötti egyenlőtlenségeket); ha a csúcsokban nem találunk semmit, kezdjünk köröket rajzolni a feltételezett helyek köré, amíg nem ér el a peremük a várak feltételezhető helyéig. Ez csak egy módszer, várom a jobb ötleteket.
Előfordulhat, hogy nem is 11szög-alakban helyezkednek el a várak, hanem más síkidomban. A történelmi, vallási vonzata a dolognak jól jöhet: ötleteket szülhet, milyen síkidomok lehetnek ezek.
A matematikai vonzat csupán a közelítés, becslés matematikája, hiszen a földi környezet nem tökéletetes, ellenben az elméletben létező euklideszi térrel. Nem szükséges a 11szög megszerkesztése; meg lehet kerülni a lehetetlent, mert a probléma nemlehetlen.
|
|
|
| [74] asinus | 2007-05-04 22:45:11 |
 Kedves Sirpi! Tökéletesen igaz, 40 db kell a 0,8181...fokos kis háromszögből, így kajuk meg a szükséges 32,72.... fokos szükséges szöget, mely végtelen tizedeseket ad. Ami a lényeg, hogy 1/440 teljes szög nem szerkeszthető. Ide akartam kilyukadni én is.
|
| Előzmény: [72] Sirpi, 2007-04-29 14:31:05 |
|
| [73] Maga Péter | 2007-04-29 19:07:06 |
 Itt nagy zavart érzek. Ugyanis a (360/17)°-kal ugyanaz a probléma lehetne, mint a (360/11)°-kal, hiszen az is végtelen, szakaszos tizedestört, szabályos 17-szög mégis szerkeszthető.
|
| Előzmény: [71] asinus, 2007-04-29 11:41:01 |
|
| [72] Sirpi | 2007-04-29 14:31:05 |
 Ha 440 részre osztjuk a teljesszöget, akkor a 11-szöghöz nyilvánvalón 40 db kell (440/11), nem pedig 48,88, szóval itt valami sántít. A gond azzal van, hogy az 1/440 teljesszög nem szerkeszthető.
|
| Előzmény: [71] asinus, 2007-04-29 11:41:01 |
|
