KöMaL Problems in Mathematics, April 2010
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'C'Deadline expired on May 10, 2010. |
C. 1030. x and y are real numbers such that x+3y=12 and x 2y
2y 0. What values may x+2y have?
0. What values may x+2y have?
(5 pont)
solution (in Hungarian), statistics
C. 1031. In the lottery, five out of the numbers 1 to 90 are drawn. Ticket holders mark five numbers on each ticket. A man bought two tickets and marked ten different numbers on them altogether. Given that four out of his ten numbers were drawn, what is the probability that he had a ticket with
a) four numbers drawn?
b) two numbers drawn?
(5 pont)
solution (in Hungarian), statistics
C. 1032. Vertices B and C of a triangle are connected to the points that divide the opposite sides into three equal parts. The connecting line segments determine a quadrilateral. Prove that the quadrilateral has a diagonal parallel to side BC.
(5 pont)
solution (in Hungarian), statistics
C. 1033. Solve the equation \(\displaystyle \log_{2010}\, (2009\, x)=\log_{2009}\, (2010\, x)\).
Suggested by J. Pataki, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 1034. A regular hexagon is rotated about its axes of symmetry. Find the ratio of the surface areas of the resulting solids.
(5 pont)
 |
Problems with sign 'B'Deadline expired on May 10, 2010. |
B. 4262. Given the points P and Q, determine the locus of the intersection of the line e passing through P with the plane Se through Q that is perpendicular to e.
(3 pont)
solution (in Hungarian), statistics
B. 4263. Solve the following simultaneous equations: x3+4y=y3+16x, .
(4 pont)
solution (in Hungarian), statistics
B. 4264. Triangle ABC has a 120o angle at vertex C. The orthocentre of the triangle is M, the centre of the circumscribed circle is O, and the midpoint of arc ACB of the circle is F. Prove that MF=FO.
(3 pont)
solution (in Hungarian), statistics
B. 4265. Find a colouring of positive integers with 7 colours such that the colours of the numbers {a,2a,3a,4a,5a,6a,7a} are pairwise different for every positive integer a.
(4 pont)
solution (in Hungarian), statistics
B. 4266. Let a1, a2, a3, a4 denote four consecutive elements in a row of Pascal's triangle. Prove that the numbers ,
,
form an arithmetic progression.
(3 pont)
solution (in Hungarian), statistics
B. 4267. Prove that the perpendiculars drawn to the sides of a triangle at the points of tangency of the escribed circles are concurrent.
Suggested by G. Holló, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 4268. What is the sixth digit following the decimal point in the decimal form of ?
(4 pont)
solution (in Hungarian), statistics
B. 4269. Construct the point P on side AB of triangle ABC for which the radii of the inscribed circles of triangles BCP and ACP are equal.
(5 pont)
solution (in Hungarian), statistics
B. 4270. Let ABCDEF be a hexagon inscribed in a circle. Prove that AD.BE.CF=AB.DE.CF+BC.EF.AD+CD.FA.BE+AB.CD.EF+BC.DE.FA.
(5 pont)
solution (in Hungarian), statistics
B. 4271. Is there a polynomial of degree at least two that represents a one-to-one mapping of the set of rational numbers onto itself?
(5 pont)
 |
Problems with sign 'A'Deadline expired on May 10, 2010. |
A. 506. Prove that for every prime p, there exists a colouring of the positive integers with p-1 colours such that the colours of the numbers {a,2a,3a,...,(p-1)a} are pairwise different for every positive integer a.
(5 pont)
A. 507. The circles \(\displaystyle K_1,\dots,K_6\) are externally tangent to the circle \(\displaystyle K_0\) in this order. For each \(\displaystyle 1\le i\le 5\), the circles \(\displaystyle K_i\) and \(\displaystyle K_{i+1}\) are externally tangent to each other, and \(\displaystyle K_1\) and \(\displaystyle K_6\) are externally tangent to each other as well, according to the Figure. Denote by \(\displaystyle r_i\) the radius of \(\displaystyle K_i\) (\(\displaystyle 0\le i\le6\)). Prove that if \(\displaystyle r_1r_4=r_2r_5=r_3r_6=1\) then \(\displaystyle {r_0\le 1}\).
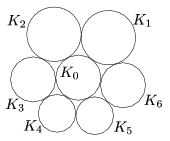
Proposed by: Balázs Strenner, Székesfehérvár
(5 pont)
A. 508. An induced subgraph \(\displaystyle S\) of the graph \(\displaystyle G\) is called ``dominant'' if every vertex of \(\displaystyle G\), outside \(\displaystyle S\), has a neighbor in \(\displaystyle S\). Does there exist such a graph which has an even number of dominant subgraphs?
Proposed by: László Miklós Lovász, Budapest
(5 pont)
Upload your solutions above.
