KöMaL Problems in Mathematics, January 2011
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 10, 2011. |
K. 277. Steve thought of a positive integer. He gave the following information about his number: If the number is divisible by 3, then it is between 50 and 59. If the number is not divisible by 4, then it is between 60 and 69. If the number is not divisible by 6, then it is between 70 and 79. Given that all his statements above are true, find out which number Steve had in mind.
(6 pont)
solution (in Hungarian), statistics
K. 278. Each of the two diagrams below shows three regular polygons (some of which are stellated polygons) that meet at a vertex. Do they really touch each other along their sides in both cases, or is there a diagram that ``lies''?
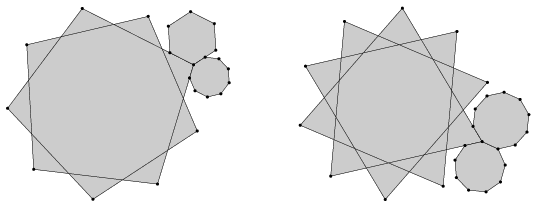
(6 pont)
solution (in Hungarian), statistics
K. 279. Ann, Belle, Carol and Dora played with a deck of 52 cards. In one game, Dora was dealing out the cards one by one to the players, starting with Ann, followed by Belle, Carol and Dora in this order, when suddenly some of the cards she had not dealt out yet slipped out of her hands and fell on the floor. The girls noticed that the number of cards on the floor was 2/3 of the number of cards Ann had already got, and the number of cards that Carol had got was 2/3 of those in the remaining part of the deck in Dora's hand that she had not dealt out yet. How many cards had Dora dealt out altogether?
(6 pont)
solution (in Hungarian), statistics
K. 280. Find the smallest natural number of the form 2a3b7c, such that the half of the number is the cube of an integer, one third of the number is the seventh power of an integer, and one seventh of the number is the square of an integer.
(6 pont)
solution (in Hungarian), statistics
K. 281. Dominique has a set of dominoes in which the stone of smallest value is a double 1, the largest value is a double 6, and there is one stone with every intermediate pair of numbers. Dominique realized that she could also represent certain fractions with her domino stones: the number on the upper domino part is the numerator and the number on the lower part is the denominator. Dominique and her sister Naomi were sitting facing each other at a table. Dominique laid the divisions between them on the table. When they checked the dominoes lying face down, they observed that the arithmetic was correct from both of their points of view. What may be the two stones lying face down?
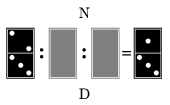
(6 pont)
solution (in Hungarian), statistics
K. 282. A triangle is built out of matchsticks. The lengths of the sides are 13, 20, and 21 matches. Find the lengths of those altitudes of the triangle (if any) that can be represented with a whole number of matchsticks.
(6 pont)
 |
Problems with sign 'C'Deadline expired on February 10, 2011. |
C. 1060. Let n denote a number divisible by 3. Every third term of the sequence n-1, n-2, ..., 2, 1 is cancelled. The subsequent pairs of terms of the remaining sequence are given alternating plus and minus signs: +(n-1), +(n-2), -(n-4), -(n-5), ... . Prove that the sum of the numbers obtained in this way is n.
(5 pont)
solution (in Hungarian), statistics
C. 1061. Construct the triangle ABC out of the following parts given: the midpoint of side AB, the foot of the altitude drawn to side AC, and the angle  lying at vertex A.
lying at vertex A.
(5 pont)
solution (in Hungarian), statistics
C. 1062. A die is rolled n times. What is the probability that there are two equal numbers among the results obtained?
(5 pont)
solution (in Hungarian), statistics
C. 1063. A vertical wall of a building is a square of side 20 metres. The angles subtended by the vertical sides of the square at two points on the (level) ground are measured. The results are 40o and 38o at one point, and 32o and 40o at the other point. Find the distance between the two points.
(5 pont)
solution (in Hungarian), statistics
C. 1064. The real numbers x, y, z, in this order, are the first three terms of a non-constant arithmetic progression. Given that cos x+cos y+cos z=1 and , find the tangent of the 12th term.
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 10, 2011. |
B. 4322. Five applicants are to be scheduled for job interviews at five given times. On an application form, each applicant was asked to mark two out of the five times. What is the probability that each of them can be interviewed at one of the two times they have marked?
(Suggested by G. Holló, Budapest)
(4 pont)
solution (in Hungarian), statistics
B. 4323. Solve the following equation: .
(3 pont)
solution (in Hungarian), statistics
B. 4324. In triangle ABC, the foot of the altitude from vertex A is D, the midpoint of the altitude from vertex B is E, and the midpoint of the altitude from vertex C is F. Show that .
(Suggested by Sz. Miklós, Herceghalom)
(4 pont)
solution (in Hungarian), statistics
B. 4325. a) Is the inequality PA+PB<CA+CB true for all interior points P of an arbitrary triangle ABC? b) Is the inequality PA+PB+PC<DA+DB+DC true for all interior points P of an arbitrary tetrahedron ABCD?
(5 pont)
solution (in Hungarian), statistics
B. 4326. Let a and b be integers. Find integers c and d such that an+c and bn+d are relative primes for all integers n.
(5 pont)
solution (in Hungarian), statistics
B. 4327. Given the median drawn to a leg and the angle enclosed by this median and the other leg, construct an isosceles triangle.
(4 pont)
solution (in Hungarian), statistics
B. 4328. A regular pentagon of side a is rotated about a side. The volume of the resulting solid of revolution equals that of the solid obtained by rotating a regular pentagon of side b about a diagonal. Determine the ratio a:b.
(3 pont)
solution (in Hungarian), statistics
B. 4329. Express the exact value of sin (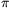 /22011) only using digits of 1 and 2, the four basic operations and square roots.
/22011) only using digits of 1 and 2, the four basic operations and square roots.
(4 pont)
solution (in Hungarian), statistics
B. 4330. Find the polynomial p of two variables, such that
(Suggested by A. Hraskó, Budapest)
(4 pont)
solution (in Hungarian), statistics
B. 4331. P is an interior point of a convex polygon . Prove that is it possible to find four lines on the plane such that for each side of
there is a line among the four for which this side lies in one of the open half planes and P lies in the other open half plane formed by the line. Is the statement also true for only three lines instead of four?
(5 pont)
 |
Problems with sign 'A'Deadline expired on February 10, 2011. |
A. 524. Is it possible to split the set {1,2,...,2010} into pairwise disjoint, 5-element subsets in such a way that the sum of elements in each subset is divisible by 2011?
(5 pont)
solution (in Hungarian), statistics
A. 525. Let be a polynomial with integer coefficients, and let
be pairwise distinct integers. Suppose that for infinitely many prime numbers p there exists an integer kp for which
Prove that there exists an integer k0 such that
(5 pont)
solution (in Hungarian), statistics
A. 526. In the Cartesian plane call those regions as strips which are bounded by two parallel lines. Define the width of a strip as the side length of the inscribed squares, with sides being parallel to the coordinate axes. Prove that if finitely many strips cover the unit square 0 x,y
x,y 1 then the sum of widths of those strips is at least 1.
1 then the sum of widths of those strips is at least 1.
(5 pont)
Upload your solutions above.
