A KöMaL 2022. októberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2022. november 15-én LEJÁRT. |
M. 416. Akasszunk egy kilincs végére egy kis méretű tárgyat, és fokozatosan növeljük a terhelést további testek ráhelyezésével. Mérjük meg a kilincs egyensúlyi szöghelyzetét a ráakasztott tömeg függvényében! A lehetséges legnagyobb szög elérése után fokozatosan csökkentsük a terhelést, és mérjük meg ebben az esetben is a szöghelyzetet a tömeg függvényében. Adatainkat ugyanazon a grafikonon ábrázoljuk!
Közli: Szász Krisztián, Budapest
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2022. november 15-én LEJÁRT. |
G. 789. Becsüljük meg, hogy mennyivel csökken testünk tömege, miközben nyolc órán keresztül, egyfolytában, nyugodtan alszunk! Használjuk a következő adatokat:
– Egy lélegzetvétel során 0,5 l levegő cserélődik ki.
– Percenként 15-öt lélegzünk.
– A kilélegzett levegő szén-dioxid-tartalma 5 V/V%.
– A kilélegzett levegő 6 V/V% vízgőzt tartalmaz.
(3 pont)
G. 790. Egy autó átlagos fogyasztása 6 liter/100 km. Teljesen üres, kanyargós, kétsávos autópályán 300 km-t tesz meg a gépkocsi. Az útszakaszon a kanyarok összhossza 50 km, a kanyarok sugara átlagosan 1 km, a sávok szélessége pedig 4 m. Becsüljük meg, hogy mennyivel csökken a jármű fogyasztása, ha egy felelőtlen sofőr minden kanyart a belső íven tesz meg!
(3 pont)
G. 791. Zsonglőrködő elméleti fizikus a következő mutatványt találja ki. Egymás tetejére helyez \(\displaystyle n\) számú, tökéletesen rugalmas labdát, közöttük igen kicsiny résekkel. A labdatornyot kemény felületre ejti, ahová a labdák \(\displaystyle v\) sebességgel érkeznek meg. A sorozatos pillanatszerű ütközések után a legfelső labda kivételével minden lejjebb lévő labda megáll, a legfelső viszont \(\displaystyle nv\) sebességgel pattan fel. Bizonyítsuk be (például a teljes indukció módszerével), hogy ez a mutatvány akkor teljesülhet, ha a labdák tömege kielégíti a következő formulát:
\(\displaystyle m_k=\frac{2m_0}{k(1+k)}, \)
ahol \(\displaystyle m_0\) a legalsó labda tömege, valamint \(\displaystyle k=1, 2, 3, \dots, (n-1), n\).
(4 pont)
G. 792. Az ábrán látható áramkörben egyforma izzólámpák vannak. A kapcsoló zárását követően az A és a B lámpa fényesebben vagy halványabban fog világítani? (Tekintsünk el az izzólámpák ellenállásának hőmérsékletfüggésétől.)
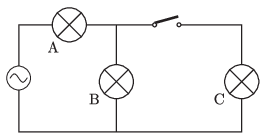
(3 pont)
 |
P-jelű feladatokA beküldési határidő 2022. november 15-én LEJÁRT. |
P. 5427. Az ábrán látható áramkörben található 230 V névleges feszültségű volfrámszálas izzólámpák egyformák, melyeknek áram–feszültség karakterisztikáját az alábbi grafikon mutatja. Az áramkörben található feszültségforrás 230 V-os.
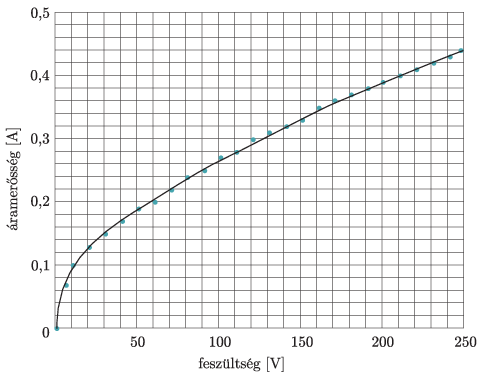
100 W-os villanykörte áram–feszültség karakterisztikája
\(\displaystyle a)\) Mekkora egy ilyen izzólámpa elektromos ellenállása a névleges feszültségen?
\(\displaystyle b)\) Mekkora ellenállású az A és a B lámpa izzószála a kapcsoló nyitott állásában?
\(\displaystyle c)\) Mekkora ellenállásúak az izzószálak a kapcsoló zárása után?
\(\displaystyle d)\) Mekkora teljesítményt adnak le az izzólámpák a fenti esetekben?

Közli: Honyek Gyula, Veresegyház
(5 pont)
P. 5428. Képzeljük el, hogy nap-éj egyenlőség idején egy egyenlítői ország tengerpartján hason fekszünk a homokban, és figyeljük a naplementét. A tenger tükörsima, az ég tiszta kék, és abban a pillanatban, amikor a Nap utolsó sugara eltűnik a horizonton, hirtelen felállunk, és így még újra láthatjuk a Nap felső karimáját. Becsüljük meg, hogy felállásunk után mennyi idővel tűnik el újra a napkorong!
Amerikai feladat nyomán
(4 pont)
P. 5429. Egy elektromos autó álló helyzetből indulva 10 s alatt egyenletes gyorsulással 108 km/h sebességet ér el. Kerekeinek sugara 0,4 m, a keréktárcsán található egy 0,2 m sugarú díszítőgyűrű. Az indulástól számítva mennyi idő múlva lesz ennek a vékony gyűrűnek olyan pontja, amely nem gyorsul? Mekkora ebben a pillanatban az autó sebessége?
Közli: Gnädig Péter, Vácduka
(5 pont)
P. 5430. A klímaváltozás egyik okaként szokták említeni az ,,intenzív hústermelést''. Egy szarvasmarha naponta 160-320 liter metángázt bocsát ki. A globális állattenyésztésben egymilliárd marhát tartanak nyilván. Becsüljük meg, hogy milyen vastag réteget alkotna az állatok egy évi metángáz-kibocsátása a Föld felszínén! (A Földet tekintsük 6370 km sugarú gömbnek.)
Közli: Simon Péter, Pécs
(3 pont)
P. 5431. Egy 10 cm sugarú, gömb alakú, homogén, tömör testnek egy bizonyos \(\displaystyle t\) tengelyre vonatkoztatott tehetetlenségi nyomatéka 10%-kal nagyobb, mint a gömb lehető legkisebb tehetetlenségi nyomatéka. Milyen messze van a \(\displaystyle t\) egyenes a gömb középpontjától? (Lásd még a ,,Merev testek mozgásegyenletei'' c. rövid cikket a KöMaL honlapján (https://www.komal.hu/cikkek/cikklista.h.shtml.)
Közli: Tornyos Tivadar Eörs, Budapest
(3 pont)
P. 5432. Egy függőleges helyzetben rögzített, vékony szigetelőpálcára három egyforma tömegű és egyenlő töltésű szigetelőgyöngyöt fűztünk fel. Az alsó gyöngy rögzített, a fölötte lévő másik kettő szabadon elcsúszhat a pálcán. Egyensúlyi helyzetben hányszor messzebb van a legfelső gyöngy a középsőtől, mint a középső a legalsótól?
Közli: Holics László, Budapest
(5 pont)
P. 5433. Egy vízzel töltött, téglatest alakú, elhanyagolható falvastagságú akvárium három függőleges oldala a vízből rájuk eső fényt visszaveri. Az akvárium szélessége \(\displaystyle d = 50\) cm, hossza \(\displaystyle L=120\) cm. Az akvárium rövidebb oldalához vízszintes síkban valamekkora beesési szögben lézersugár érkezik. Az ábra felülnézetet mutat. (A víz törésmutatója: \(\displaystyle n=4/3\).)
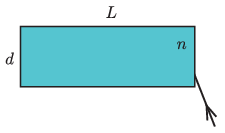
A kilépő fénysugár – többszöri tükröződés után – éppen a beeső fénysugárral párhuzamosan haladva hagyja el az akváriumot. Legfeljebb hány tükröződés történhetett?
Zsigri Ferenc (Budapest) feladata nyomán
(5 pont)
P. 5434. Az ábrán szereplő feszültségforrás elektromotoros ereje bekapcsolás után időben lineárisan növekszik fel a kezdeti 0 voltos értékről; \(\displaystyle U(t)=U_0\frac{t}{t_0}\). A \(\displaystyle K\) kapcsoló segítségével bármelyik pillanatban rákapcsolható a feszültségforrás az áramkörre. A feszültségforrás bekapcsolása után mennyi idővel kell zárni a kapcsolót, hogy ezután az ellenálláson átfolyó áram erőssége időben lineárison nőjön? Milyen ütemben nő ekkor az áramerősség?
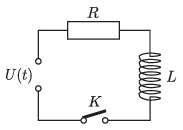
Közli: Széchenyi Gábor, Budapest
(5 pont)
P. 5435. Egy cső belső sugara \(\displaystyle R\), tengelye \(\displaystyle \alpha\) szöget zár be a vízszintessel. A csövet állandó \(\displaystyle \omega\) szögsebességgel forgatjuk a tengelye körül.
A csőbe egy pontszerűnek tekinthető, kicsiny testet helyezünk. A cső fala és a kis test közötti csúszási súrlódási együttható \(\displaystyle \mu\) (\(\displaystyle \mu>\tg\alpha\)). Azt tapasztaljuk, hogy kellően hosszú idő elteltével a kis test egyenes vonalú egyenletes mozgást végez. Mekkora a mozgás sebessége?
Közli: Balogh Péter, Gödöllő
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
