A KöMaL Ifjúsági Ankét programja
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Az elõadások rövid ismertetõi
Lóczi Lajos: Stephen Wolfram: A New Kind of Science
(Könyvismertetõ elõadás)
Stephen Wolfram könyve több mint egy évtizedes munka után elkészült. Az 1980-as években sejtautomatákkal végzett kísérleteire alapozva, valamint az általa kifejlesztett Mathematica számítógépes programnyelv segítségével csaknem 1100 oldal elõkészítés, és számtalan, a legkülönfélébb tudományterületrõl vett példa után érkezünk el a könyv központi mondanivalójához: a számítási ekvivalencia-elvhez (Principle of Computational Equivalence), amely többek között azt állítja, hogy egy bizonyos szinten túl bármely két rendszer bonyolultsága azonos.
A New Kind of Science olvasmányosan megírt könyv, és egyaránt szól specialistáknak, illetve laikusoknak. Az elmúlt évszázadok egyenletei helyett a hangsúly mindvégig az algoritmuson van. Állandóan végigvonuló motívum, hogy nagyon egyszerû szabályok mennyire összetett rendszereket képesek létrehozni. Wolfram azt jósolja, hogy szemléletmódja komoly kihatással lesz az egész tudományra, illetve tudományos gondolkodásunkra.
Szilassi Lajos: Szabályos toroidok
Mint ismert, a szabályos poliéderek minden csúcsába ugyanannyi él fut be, és minden lapjának ugyanannyi éle van. Egy poliéder topológiailag szabályos, ha további (pl. az élek és lapok szögeire vonatkozó) követelményeket nem kötünk ki.
Ilyen - topológiailag szabályos - poliéderek nem csak a gömbbel homeomorf egyszerû poliéderek körében léteznek.
Egy közönséges poliédert toroidnak nevezünk, ha topológiailag tórusz-szerû, (azaz folytonos deformálással tórusszá alakítható) és minden lapja egyszerû sokszög.
Egy toroidot szabályosnak nevezünk, ha minden csúcsába ugyanannyi él fut be, és minden lapja ugyanannyi oldalú egyszerû (de nem feltétlenül konvex) sokszög.
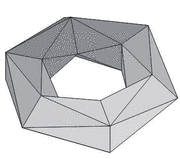
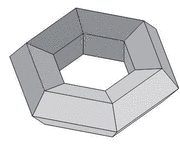
Könnyen belátható, hogy a szabályos toroidok három osztályba sorolhatók aszerint, hogy az egy csúcsra ill, egy lapra hány él illeszkedik.
 |
 |
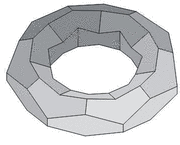 |
| A szabályos toroidok három osztályának egy-egy reprezentánsa | ||
Mindhárom osztályba végtelen sok toroid tartozik, a lapok, ill. csúcsok száma tetszõlegesen nagy lehet. Ezért elsõsorban azt vizsgáljuk, hogy melyek azok a szabályos toroidok, amelyekben a lapok, ill. csúcsok száma minimális, vagy egyéb különleges tulajdonsággal rendelkeznek.
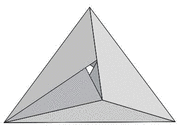
E poliéderek közül különös figyelmet érdemel az un. Császár-poliéder, amelynek nincs átlója, azaz bármely két csúcsa szomszédos, valamint ennek a (topológiai értelemben vett) duálisa, az un. Szilassi-poliéder, amelynek bármely két lapja szomszédos. Ez utóbbit e sorok írója fedezte fel 1977-ben.
 |
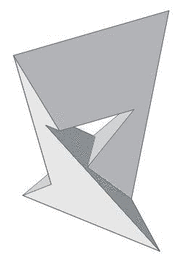 | |
| A Császár- és a Szilassi-poliéder | ||
Kós Géza: Alakzatok egymásba mozgatása a síkban
Egy olyan algoritmust mutatunk be, amely két, azonos topológiájú síkbeli alakzat egymásba mozgatására, ezáltal például különbözõ animációk készítésére alkalmazható. A két, egymásba átvivendõ alakzat pontokból és a pontokat összekötõ szakaszokból állhat, a szakaszok nem metszhetik egymást.
Az algoritmus Michael S. Floater, Craig Gotsman és Vitaly Surazhsky munkáira épül. A két alakzatot egy közös, konvex sokszögekre bontott struktúrába ágyazzuk be úgy, hogy a két helyzet csupán a pontok helyzetében különbözik. A közbülsõ állapotokat egy paraméteres lineáris egyenletrendszer határozza meg.
Véletlen - tudományos ismeretterjesztõ táncjáték
A KöMaL Ifjúsági Ankét zárórendezvénye 2002 december 22. vasárnap este 8 órakor a MU Színházban (XI. ker. Kõrösy J. u. 17. tel:466-4627)

Játék agyból és gyomorból.
Mi a véletlen? Tán nem is létezik? Tán ha elég okosak és gyorsak volnánk, ahogy lendül a kéz, ahogy perdül a kocka ki tudnánk számítani mielõtt leér, hogy melyik oldalát mutatja majd fölfelé? A véletlen csak tudatlanságunk mércéje? Vagy a véletlen létünk alapja, világunk szabadsága, a szél, mely az emberiség hajójának vitorláit dagasztja? Egy bölcs - vagy épp hogy részeges - kormányos?
Nézünk a véletlenre agyból és gyomorból. Tán majd egymást látjuk.
| Rendezõ: | Szabó Réka |
| Elõadó: | Mérõ László |
| Koreográfia, tánc: | Csákvári Gyula, Jarovinszkij Vera, Kopeczny Kata, Ladjánszki Márta, Szabó Réka, Szász Dániel |
| Zene: | Márkos Albert |
| Kosztüm: | Pillangó |
| Fény: | Németh Richárd, Payer Ferenc |
| Haj: | Szarka Betti, Bagyánszki Ákos |
Támogatók: L1 Független Táncmûvészek Társulása, NKA, Fõvárosi Közgyûlés Kulturális Bizottsága, Soros Alapítvány
Az elõadás zártkörû, tiszteletjegyek korlátozott számban igényelhetok a KöMaL szerkesztõségében: 1117 Budapest, Pázmány P. sétány 1/A. V.em. 5.106. Tel: 372-2850. e-mail: szerk@komal.hu

