A C. 1313. feladat (2015. október)

C. 1313. Egy egyenlő oldalú háromszög egyik csúcsa a $\displaystyle (0;1)$ pont. Két további csúcsa közül az egyik az $\displaystyle x$ tengelyen, a másik az $\displaystyle y=3$ egyenletű egyenesen van. Mekkora a háromszög területe?

(5 pont)

A beküldési határidő 2015. november 10-én LEJÁRT.

Megoldás. Készítsünk ábrát. Két ilyen háromszög van, melyek az $\displaystyle y$ tengelyre szimmetrikusan helyezkednek el, így egybevágóak és területük is egyenlő. Tekintsük az $\displaystyle x$ tengely pozitív felén elhelyezkedő háromszöget.

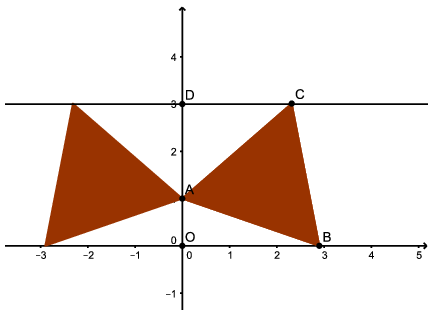
A $\displaystyle C$ csúcs koordinátái $\displaystyle (c;3)$, a $\displaystyle B$ csúcsé pedig $\displaystyle (b;0)$. Az $\displaystyle AB$ oldal hosszának négyzete $\displaystyle 1+b^2$, az $\displaystyle AC$ oldalé $\displaystyle (3-1)^2+c^2=4+c^2$, végül a $\displaystyle BC$ oldalé $\displaystyle (b-c)^2+(0-3)^2=(b-c)^2+9$. Az $\displaystyle ABC$ háromszög területét legegyszerűbben úgy számolhatjuk ki, ha a DOBC trapéz területéből kivonjuk az $\displaystyle AOB\triangle$ és az $\displaystyle ACD\triangle$ területét: $\displaystyle t_{ABC}=t_{DOBC}-t_{AOB}-t_{ACD}=\frac{(b+c)\cdot3}{2}-\frac b2-\frac{2c}{2}=\frac c2+b$.

Mivel az $\displaystyle ABC$ háromszög szabályos, ezért oldalai egyenlőek, és így $\displaystyle 1+b^2=4+c^2$, amiből $\displaystyle b=\sqrt{3+c^2}$; illetve (ezt felhasználva) $\displaystyle 4+c^2=(b-c)^2+9=b^2+c^2-2bc+9=3+2c^2-2\sqrt{3+c^2}\cdot c+9$. Ebből $\displaystyle 2c\sqrt{3+c^2}=c^2+8$, amit négyzetre emelve: $\displaystyle 4c^2(3+c^2)=(c^2)^2+16c^2+64$. Rendezve egy $\displaystyle c^2$-re másodfokú egyenletet kapunk: $\displaystyle 3(c^2)^2-4c^2-64=0$, amiből

$\displaystyle c^2_{1,2}=\frac{4\pm\sqrt{16+4\cdot3\cdot64}}{6}=\frac{4\pm 28}{6},$

a nemnegatív megoldás a $\displaystyle c^2=\frac{16}{3}$. Vagyis $\displaystyle c=\frac{4}{\sqrt3}$, és így $\displaystyle b=\sqrt{3+\frac{16}{3}}=\frac{5}{\sqrt3}$.

A terület ebből $\displaystyle \frac c2+b=\frac{2}{\sqrt3}+\frac{5}{\sqrt3}=\frac{7}{\sqrt3}$.

Statisztika:

70 dolgozat érkezett.
5 pontot kapott:	Balázs Ákos Miklós, Bánóczi Anna, Barczikai Noémi, Csapó Márton, Csorba Benjámin, Dér Boglárka, Fischer Kornél, Fülöp Ágota, Fülöp Botond, Galbács Márton, Gera Dóra, Horváth András János, Horváth Tibor 1998, Karajz Ágnes Fruzsina, Kasó Ferenc, Kelkó Balázs, Kiss Vivien Mercédesz, Kocsis Júlia, Kósa Szilárd, Márkus Tamás, Matusek Márton, Nagy 911 Viktória, Ondrik Ákos, Pécz Bálint, Révy Gábor, Sallai Krisztina, Sipeki Gergely, Souly Alexandra, Sudár Ákos, Szabó Alexandra, Szajkó Gréta, Szalay Máté Csongor, Szűcs Győző, Szücs Patrícia, Tar Viktor, Tolmácsi Ágnes, Tóth Adrián, Török Attila, Török Réka , Varga 888 Lili, Viharos Loránd Ottó.
4 pontot kapott:	10 versenyző.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	6 versenyző.

A KöMaL 2015. októberi matematika feladatai