KöMaL Problems in Mathematics, March 2009
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on April 10, 2009. |
K. 205. Jack and Jill are going to the gingerbread house 20 km from their home. The two of them have one bicycle together. The bicycle can only bear one rider at a time. They decide that Jack will walk first and Jill will go by bike to some point along the way where she puts the bike down and continues on foot. When Jack reaches that point, he will get on the bike and cycle to the gingerbread house. Jack's speed is 5 km/h on foot and 12 km/h by bike. Jill walks at 4 km/h and bikes at 10 km/h. If they start out together, how many kilometers should Jill cover by bike so that they get to the gingerbread house at the same time?
(6 pont)
solution (in Hungarian), statistics
K. 206. Steve and Charlie are brothers. Their mom bought them petits fours at the confectioner's shop. There are 8 larger cubes of edge 3 cm and 27 smaller cubes 2 cm on edge. Five faces of each cake are covered with icing that has the same uniform thickness on all of them. The bottom of the cakes is not iced. Steve and Charlie would like to divide the petits fours between them so that each gets the same total volume, the cakes are not cut in pieces, and each of them gets both kinds.
a) Show that these conditions are impossible to meet.
b) When they see that they cannot divide the petits fours equally by volume, they decide to have equal quantities of icing instead. (They still do not want to cut the cakes, and each of them should get both kinds.) Find all possible ways to divide the petits fours.
(6 pont)
solution (in Hungarian), statistics
K. 207. The floor of a rectangular shaped hallway of area 14.4 m2 is tiled with rectangular tiles. In every fifth row of tiles along the length of the hallway, the tiles are rotated through a right angle. In this way, 15 rows of tiles are needed and no tiles need to be cut. If all tiles were laid in the way they are laid in the fifth rows, the hallway could also be tiled without cutting any tiles. In that case, there would be 18 rows of tiles. What may be the dimensions of the tiles if their sides in centimetres are whole numbers?
(6 pont)
solution (in Hungarian), statistics
K. 208. a) In the coordinate plane, a circle of radius 5 is drawn about the origin. How many lattice points lie on the circumference of the circle? (A lattice point is a point whose coordinates are both integers.)
b) Find an integer r, such that there are more than 14 lattice points on a circle of radius r centred at the origin. Justify your answer.
(6 pont)
solution (in Hungarian), statistics
K. 209. An ice cream vendor is constructing a shade out of wood around the top of his ice cream booth. One figure shows what the shade will look like, and the other figure shows a view from above. The plane of each piece of the shade encloses a 45o angle with the appropriate vertical wall of the booth. The base of the booth is a square of side 3 m. The shade stretches out to a horizontal distance of 1 m from the walls. How many m2 of wooden plate is needed to construct the shade?
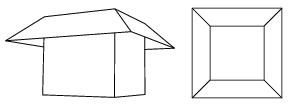
(6 pont)
solution (in Hungarian), statistics
K. 210. The Figure shows a part of little Dorothy's bicycle. The centre of the rear wheel is A and the pedal lever TK (with one of the pedals at its endpoint K) rotates about point T. Assume that the points A, K, T are coplanar. The length of TK is 20 cm and the length of AT is 48 cm. As the lever turns around point T, how many positions does the point K have in which the distance AK in centimeters is a whole number and the triangle AKT is acute-angled?
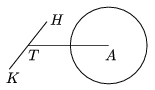
(6 pont)
 |
Problems with sign 'C'Deadline expired on April 15, 2009. |
C. 980. Assume that there are relatively more teenagers among allergic people than in the whole population, and a higher proportion of teenagers do sports than the population average. Does it follow that there are relatively more allergic people among those doing sports?
(5 pont)
solution (in Hungarian), statistics
C. 981. The captain of a ship wrote down the formula in his log book for the distance to the horizon. Unfortunately, the number p got blurred. d denotes the distance to the horizon in kilometers, and h stands for the height of the eyes of the observer above sea level in metres. Determine a value of p that provides a practicable formula. (Use 6370 km for the radius of the Earth.)
(5 pont)
solution (in Hungarian), statistics
C. 982. Prove that 52008+4 is a composite number.
(5 pont)
solution (in Hungarian), statistics
C. 983. Given the line BD and the feet of the perpendiculars dropped from point A onto line CD, from point B onto line DA, from point C onto line AB and from point D onto line BC, construct the quadrilateral ABCD. (It is not required to discuss the number of possible solutions.)
(5 pont)
solution (in Hungarian), statistics
C. 984. a, b and c are three not necessarily consecutive terms of an arithmetic progression of positive numbers. Given that , find the common difference of the arithmetic progression.
(5 pont)
 |
Problems with sign 'B'Deadline expired on April 15, 2009. |
B. 4162. 60 bars of chocolate are distributed among a class of 30 students. Everyone gets at least one but no one gets 31 bars. Prove that it is possible to select a group of students who received a total of exactly 30 bars of chocolate together.
(4 pont)
solution (in Hungarian), statistics
B. 4163. A cuboid is built out of 5×10×20-cm bricks without leaving any gaps between them. Prove that the same cuboid can also be built out of the same bricks with all edges of equal lengths being parallel.
(4 pont)
solution (in Hungarian), statistics
B. 4164. Prove that if a triangle can be constructed from every three line segments selected out of a set of 5, then there exist three line segments in the set that form an acute-angled triangle.
(3 pont)
solution (in Hungarian), statistics
B. 4165. The diagonals of a convex quadrilateral ABCD intersect at O. Prove that AB2+BC2+CD2+DA2=2(AO2+BO2+CO2+DO2) is true if and only if the diagonals AC and BD are perpendicular or one of them has its midpoint at O.
Kvant
(3 pont)
solution (in Hungarian), statistics
B. 4166. Construct a point D on the side BC of triangle ABC, such that the inscribed circles of triangles ABD and ACD touch each other on the line AD.
(3 pont)
solution (in Hungarian), statistics
B. 4167. For every positive integer n, let f(n) denote the number obtained by reversing the order of digits in the decimal form of n. (For example, f(2500)=52, f(1456)=6541.) Find all positive integers k, such that for any multiple n of k, k also divides the number f(n).
(5 pont)
solution (in Hungarian), statistics
B. 4168. The centre of the inscribed circle of triangle ABC is K, the midpoint of side AB is F, and the point of tangency of the escribed circle on side AB is G. Prove that the lines CG and KF are parallel.
(4 pont)
solution (in Hungarian), statistics
B. 4169. Prove that if a, b, c are pairwise distinct positive integers then
S=(42a+43b+43c)3+(43a+42b+43c)3+(43a+43b+42c)3
-3(42a+43b+43c)(43a+42b+43c)(43a+43b+42c)
is divisible by 128 but is not a perfect power of 2.
Suggested by D. Nagy
(5 pont)
solution (in Hungarian), statistics
B. 4170. A plane intersects the edges AB, BC, CD and AD of a tetrahedron ABCD at points K, L, M and N, respectively. Prove that .
(5 pont)
solution (in Hungarian), statistics
B. 4171. In every second, the probability that a certain bacterium will die is p and the probability that it will divide into two identical bacteria is 1-p. (The offsprings will die or divide independently of each other.) What is the probability of extinction?
(5 pont)
 |
Problems with sign 'A'Deadline expired on April 15, 2009. |
A. 476. Let n 3 be an odd integer, and let A={0,1,...,n-1} denote the set of residual classes modulo n. Call a non-empty subset B
3 be an odd integer, and let A={0,1,...,n-1} denote the set of residual classes modulo n. Call a non-empty subset B A a Dutch set, if for every a
A a Dutch set, if for every a A and for every b
A and for every b B at least one of b+a and b-a lies in B. Determine the smallest possible cardinality of a Dutch set in terms of n.
B at least one of b+a and b-a lies in B. Determine the smallest possible cardinality of a Dutch set in terms of n.
Proposed by: Gerhard Woeginger, Amsterdam
(5 pont)
A. 477. Let G be the complete graf with 2n vertices, and suppose that S1,...,Sk are subgraphs of G with the following properties:
(a) Every Si is a complete bipartite graph;
(b) Every edge of G is contained by an odd number of subgraphs Si.
Show that k n.
n.
(5 pont)
solution (in Hungarian), statistics
A. 478. If a1,a2,...,an are positive numbers with a1+a2+...+an=1, prove .
(5 pont)
Upload your solutions above.
