KöMaL Problems in Mathematics, September 2012
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on October 10, 2012. |
K. 337. How many five-digit numbers of the form are divisible by 45 if a, b and c denote different digits?
(6 pont)
solution (in Hungarian), statistics
K. 338. Which pairs of the six (3 interior and 3 exterior) angle bisectors of a triangle may be perpendicular?
(6 pont)
solution (in Hungarian), statistics
K. 339. 2/3 of the male members of a tennis club are entering a tournament in a mixed double, together with some female member of the club. The others are only playing in the singles competition. 3/8 of the women are playing in mixed doubles with some male member while the others are only entering for the singles. What fraction of the members of the club are playing singles only?
(6 pont)
solution (in Hungarian), statistics
K. 340. A large cube is built out of small white cubes, and then the faces of the large cube are painted blue. The large cube is then taken apart again. What is the size of the large cube if the number of small cubes with an even number of blue faces is the same as those with an odd number of blue faces?
(6 pont)
solution (in Hungarian), statistics
K. 341. Four congruent unit squares are separated by gaps of unit width as shown in the figure. Find the shortest path from A to B that touches each square. (It is not allowed to enter the interior of the squares.)

(6 pont)
solution (in Hungarian), statistics
K. 342. Triangle ABC in the figure is equilateral, AP bisects the angle at A. Prove that AP=BP+PC.
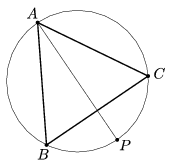
(6 pont)
 |
Problems with sign 'C'Deadline expired on October 10, 2012. |
C. 1130. Show that the last two digits of a perfect square cannot be both odd.
(5 pont)
solution (in Hungarian), statistics
C. 1131. ABCD is a convex quadrilateral. Prove that if and the angles at A and B are acute angles then AC2+BD2=AD2+BC2+2.AB.CD.
(5 pont)
solution (in Hungarian), statistics
C. 1132. Which of the fractions
is greater?
(5 pont)
solution (in Hungarian), statistics
C. 1133. The digits of the sixth power of a natural number in ascending order are as follows: 0, 2, 3, 4, 4, 7, 8, 8, 9. Which number is it?
(5 pont)
solution (in Hungarian), statistics
C. 1134. One base of an isosceles trapezium is three times the height, and the other base is two times the height. With a line parallel to one leg, the trapezium is divided into a parallelogram and an isosceles triangle. The diagonals of the trapezium and of the parallelogram are drawn. Prove that the area of the triangle bounded by the diagonals is 1/25 of the area of the trapezium.
(5 pont)
 |
Problems with sign 'B'Deadline expired on October 10, 2012. |
B. 4462. Processed cheese is often sold in small blocks of eight identical cylindrical sectors packed together in a cylindrical box (see the figure). Each small block is individually wrapped and has a label on top. We have two boxes of such cheese: one box with peperoni flavour and another with bear's leek flavour. The boxes are turned over so that the contents are mixed on the table. Then the 16 blocks are returned to the boxes in a random arrangement (with labels all facing upwards). In how many different ways is that possible if arrangements obtained from each other by rotation are not considered different but the two boxes are distinguished?
Suggested by L. Koncz, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 4463. In the Four-square Round Forest, trees form a regular triangular lattice. Is it possible to build a fence around a rectangular part of the forest such that the vertices of the rectangle are lattice points and the number of lattice points on the boundary of the rectangle is the same as in the interior?
(4 pont)
solution (in Hungarian), statistics
B. 4464. What is the sum of the digits in the cube of the number that consists of n digits of 9?
(3 pont)
solution (in Hungarian), statistics
B. 4465. The line segment A0A10 is divided into 10 equal parts. The dividing points are in this order. The third vertex of the regular triangle drawn over the line segment A8A10 is B. Show that
 BA0A10+
BA0A10+ BA2A10+
BA2A10+ BA3A10+
BA3A10+ BA4A10=60o.
BA4A10=60o.
Suggested by Sz. Miklós, Herceghalom
(4 pont)
solution (in Hungarian), statistics
B. 4466. Is there a positive integer n such that each root of the equation (4n2-1)x2-4n2x+n2=0 can be represented as a finite decimal?
(3 pont)
solution (in Hungarian), statistics
B. 4467. Solve the equation .
(5 pont)
solution (in Hungarian), statistics
B. 4468. Consider two circular discs that have no common points. The circle drawn on the line segment connecting their centres as diameter intersects each of the common exterior tangents at two points. Prove that the diagonals of the quadrilateral formed by the four points of intersection are the common interior tangents.
Suggested by V. Gedeon, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 4469. The interior angle bisectors of triangle ABC intersect the opposite sides at A1, B1, C1. Prove that the area of the triangle A1B1C1 cannot be greater than one fourth of the area of triangle ABC.
(5 pont)
solution (in Hungarian), statistics
B. 4470. The cube ABCDEFGH is standing on the table. Three vertical edges are divided by the points K, L and M in ratios of 1:2, 1:3 and 1:4, respectively, as shown in the figure. The plane KLM divides the cube into two parts. What is the ratio of the volumes of the two parts?
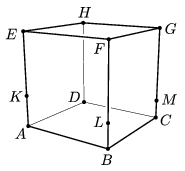
(5 pont)
solution (in Hungarian), statistics
B. 4471. Find those polynomial functions of integer coefficients that assign a positive prime number to every Fibonacci number. (The sequence Fn of Fibonacci numbers is defined by the recurrence relation Fn=Fn-1+Fn-2 with seed values F0=0, F1=1.)
(6 pont)
 |
Problems with sign 'A'Deadline expired on October 10, 2012. |
A. 566. (a) Prove that if n 2 and the product of the positive real numbers
2 and the product of the positive real numbers is 1 then
. (b) Show an example for an integer n
 2 and positive real numbers
2 and positive real numbers having product 1 that satisfy
.
(5 pont)
A. 567. (a) Find all pairs (a,b) of relatively prime positive integers a, b such that b divides a2-3 and a divides b2-3. (b) Find all pairs (a,b) of relatively prime positive integers a, b such that b divides a2-5 and a divides b2-5.
Proposed by: J. Pelikán, Budapest
(5 pont)
solution (in Hungarian), statistics
A. 568. Given a triangle ABC and a line  through its incenter. Denote by A', B' and C' the mirror images of A, B and C about
through its incenter. Denote by A', B' and C' the mirror images of A, B and C about  , respectively. Let the lines through A', B' and C', parallel to
, respectively. Let the lines through A', B' and C', parallel to  , meet the lines BC, CA and AB at P, Q and R, respectively. Prove that the points P, Q and R lie on a line and this line is tangent to the incircle.
, meet the lines BC, CA and AB at P, Q and R, respectively. Prove that the points P, Q and R lie on a line and this line is tangent to the incircle.
(5 pont)
Upload your solutions above.
