KöMaL Problems in Mathematics, February 2013
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on April 10, 2013. |
K. 367. A school organized an ice cream building competition for the students. The participants built their ice cream towers on 10-cm tall cones, by placing the scoops one by one on top of each other. Initially, each scoop was a spherical ball of 4-cm diameter, but they were compressed under the weight of the overlying balls. The height of a ball decreased by 1 mm owing to each ball on top of it. The prize winning ice cream tower was 47.5 cm tall, measured from the bottom of the cone to the top of the uppermost ball, and one third of the height of the lowermost ball was inside the cone. How many balls were used to build this tower?
(6 pont)
solution (in Hungarian), statistics
K. 368. A square sheet of paper was cut into two equal parts along a line parallel to its side. Then one of the pieces was cut into three equal parts along lines parallel to its shorter side, and the other piece was cut into three equal parts along lines parallel to its longer side. The total perimeter of the resulting six sheets is 72 cm. What is the perimeter of the original square in centimetres?
(6 pont)
solution (in Hungarian), statistics
K. 369. At the beginning of a business meeting, everyone exchanged business cards with everyone. Mr. George joined the company later on. Since he knew some of the participants, he only gave his card to those he did not know, but he did not receive a card from anyone. Thus the total number of cards given out increased by 12.5% relative to the situation before his arrival. How many participants were there after the arrival of Mr. George?
(6 pont)
solution (in Hungarian), statistics
K. 370. The sides of a triangle are 4.4 cm, 5.5 cm and 7.7 cm long. One side of a similar triangle is 15.4 cm. What may be the perimeter of the second triangle?
(6 pont)
solution (in Hungarian), statistics
K. 371. The roots of the equation x3+4x2-7x-10=0 are -5; -1 and 2. What are the roots of the equation (x-3)3+4(x-3)2-7x+11=0?
(6 pont)
solution (in Hungarian), statistics
K. 372. With lines parallel to the diagonals, a cross is drawn in a square of side 10 cm, as shown in the diagram. The lines forming the boundary of the cross inside the square intersect the sides at equal distances from the vertices. What is the distance between the parallel lines forming a particular branch of the cross if the area of the cross is 64 cm2?
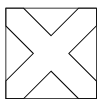
(6 pont)
 |
Problems with sign 'C'Deadline expired on March 11, 2013. |
C. 1155. A die is rolled three times. What is the probability that the product of the resulting numbers is 12?
Suggested by Z. Rimay, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 1156. The diagram shows a sketch of a crescent-shaped pendant with line symmetry. The crescent is bounded by a semicircle of radius 20 mm and another circular arc of radius 25 mm. Determine the radius of the shaded circles.
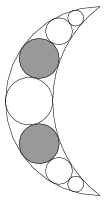
(5 pont)
solution (in Hungarian), statistics
C. 1157. For what value of the real parameter a will the equation have two equal roots?
(5 pont)
solution (in Hungarian), statistics
C. 1158. A kite-shaped plot of land has three interior angles of 80o. Its area is 900 m2. What length of fencing is needed around the whole plot?
(5 pont)
solution (in Hungarian), statistics
C. 1159. Consider all non-congruent rectangles whose side lengths are two distinct elements selected from the set . What is the total area of all such rectangles?
(5 pont)
 |
Problems with sign 'B'Deadline expired on March 11, 2013. |
B. 4512. A digit is written on each face of two cubes such that the number of any day of a month is obtained by placing the two cubes next to each other in an appropriate way. (One-digit numbers are written as usual, e.g. 01. A 9 may also be obtained by turning a 6 around.) In how many different ways can this be done if the relative positions of numbers on the same cube are not considered?
Suggested by A. Balga, Budapest
(3 pont)
solution (in Hungarian), statistics
B. 4513. The radius of the circumscribed circle of an isosceles triangle of unit base is also unity. The diameter parallel to the base of the triangle cuts off a smaller triangle. Find the exact lengths of the base and legs of the smaller triangle.
Suggested by A. Balga, Budapest
(3 pont)
solution (in Hungarian), statistics
B. 4514. Solve the equation 36a4+b4=9c4+4d4 on the set of integers.
Suggested by Gy. Orosz, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 4515. If a token is inserted in a slot machine, it will roll a regular die and show the result. Then the player may choose to either accept the prize, which is 100 times the number rolled, and thereby end the game, or to insert a second token. In the latter case, the machine rolls the die again, and then the prize is 100 times the product of the two numbers rolled. The game then ends, there is no more choice offered. How much should a token cost so that, in the long run, the slot machine make a profit for its owner?
(4 pont)
solution (in Hungarian), statistics
B. 4516. In a triangle ABC, tan  =2, tan
=2, tan 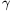 =1, and b=12. The midpoints of the sides opposite to A and B are Fa and Fb, and the feet of the corresponding altitudes are Ta and Tb, respectively. Prove that the centroid and the orthocentre of triangle ABC are collinear with the intersection of TaFb and FaTb.
=1, and b=12. The midpoints of the sides opposite to A and B are Fa and Fb, and the feet of the corresponding altitudes are Ta and Tb, respectively. Prove that the centroid and the orthocentre of triangle ABC are collinear with the intersection of TaFb and FaTb.
(4 pont)
solution (in Hungarian), statistics
B. 4517. A B are interior points of the quadrant XY centred at O. The parallels drawn to the line OX through the points A, B intersect the radius OY at the points AY and BY. The lines drawn parallel to line OY intersect the radius OX at AX and BX. Determine the total area of the quadrilaterals AAXBXB and AAYBYB as a function of the length AB.
B are interior points of the quadrant XY centred at O. The parallels drawn to the line OX through the points A, B intersect the radius OY at the points AY and BY. The lines drawn parallel to line OY intersect the radius OX at AX and BX. Determine the total area of the quadrilaterals AAXBXB and AAYBYB as a function of the length AB.
Suggested by Gy. Károlyi, Budapest, Brisbane
(4 pont)
solution (in Hungarian), statistics
B. 4518. Let n 2 be an even number, and let 0<k<n be an integer. Find the smallest number e with the following property: If a simple graph on n points has at least e edges then it contains k pairwise edge-disjoint perfect matchings.
2 be an even number, and let 0<k<n be an integer. Find the smallest number e with the following property: If a simple graph on n points has at least e edges then it contains k pairwise edge-disjoint perfect matchings.
Suggested by P. Maga, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 4519. The altitudes of a tetrahedron ABCD all pass through the point M. Let R denote the radius of the circumscribed sphere. Show that MA2+MB2+MC2+MD2=4R2.
(5 pont)
solution (in Hungarian), statistics
B. 4520. Given the positive numbers a, b and c, determine the values of the non-negative variables x, y, z such that the expression is a minimum.
Based on a problem by Gy. Szöllősy, Máramarossziget
(6 pont)
solution (in Hungarian), statistics
B. 4521. C is an interior point of a segment AB of line e. k1, k2 and k3 are semicircles drawn over the line segments AB, AC and CB on the same side of line e. The midpoints of the arcs of the semicircles are F1, F2 and F3. A circle touches semicircle k1 on the inside at E, and also touches the semicircles k2 and k3 on the outside. Show that the midpoint M of the line segment AB and the points C, F1, F2, F3 and E are all concyclic.
Suggested by Sz. Miklós, Herceghalom
(6 pont)
 |
Problems with sign 'A'Deadline expired on March 11, 2013. |
A. 581. In the plane, there are given two circles k1 and k2 with different radii, and a point O lying outside the circles. The end-points of the tangents drawn from O to k1 are P and Q, the end-points of the tangents drawn from O to k2 are R and S. The points P, Q, R, S are distinct. Let H be the external homothety center between k1 and k2. Prove that if PR is not a external common tangent to the circles but passes through H then QS also passes through H.
(5 pont)
A. 582. Let p be a fixed positive prime. For any polynomial f(x) with integer coefficients, let f*(x)=f((1+x)p-1). Find all polynomials g with integer coefficients for which the following holds: for every positive integer n there is a polynomial f with integer coefficients such that the coefficients of g-(f-f*) with degree less than n are all divisible by pn.
Proposed by: Péter Maga, Budapest
(5 pont)
solution (in Hungarian), statistics
A. 583. There are given n random events (n 3) such that each of them has probability
3) such that each of them has probability , the joint probability of each two is
and the joint probability of each three is
. (a) Prove that the probability that none of the events occurs is at most
. (b) Show that there are infinitely many numbers n, for which the events can be specified in such a way that the probability that none of the events occurs is precisely
.
Based on problem 3 of the Kürschák competition in 2012
(5 pont)
Upload your solutions above.
