KöMaL Problems in Mathematics, March 2014
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on April 10, 2014. |
K. 415. Students played with dice in the maths club. 40% of the dice were red, the rest of them were green. Next time, the number of red dice was increased by 10%, and the number of green dice was reduced by 5%. By what percentage did the number of dice change?
(6 pont)
solution (in Hungarian), statistics
K. 416. Given that , determine the digits a, b, c. (
is a six-digit number, and
is a four-digit number, where identical letters denote identical digits.)
(6 pont)
solution (in Hungarian), statistics
K. 417. A confectioner's shop sells four kinds of cakes: cheese, walnut, poppy seed and chocolate. The number of cakes on stock is 162 without the cheese cakes, 158 without the walnut cakes, 150 without the poppy seed cakes, and 160 without the chocolate cakes. How many cakes of each kind are there on stock?
(6 pont)
solution (in Hungarian), statistics
K. 418. What is the number of students in a certain class, written in base-ten notation, if the number of students as represented in some other base is 100, 32 of which are boys and 24 are girls?
(6 pont)
solution (in Hungarian), statistics
K. 419. Six congruent circles are drawn in a circular ring such that each of them touches the circles bounding the ring, and also touches the two adjacent circles. What percentage of the area of the ring is covered by the circles?
(6 pont)
solution (in Hungarian), statistics
K. 420. Alex drives 63 km to work each morning. If he starts 20 minutes later than usual, his journey will take 40% more time because of the traffic jam, and thus his average speed is reduced to 36 km/h. How long does Alex take to drive to work if he starts at the usual time?
(6 pont)
 |
Problems with sign 'C'Deadline expired on April 10, 2014. |
C. 1217. Prove that it is possible to select four out of any seven integers such that their sum is divisible by 4.
(5 pont)
solution (in Hungarian), statistics
C. 1218. On a circular table of radius 80 cm, the square tablecloth has been pulled aside, such that one corner lies exactly on the edge of the table, and the two sides that meet at the opposite vertex are tangent to the edge of the table. Determine the length of the side of the tablecloth to the nearest millimetre.
(5 pont)
solution (in Hungarian), statistics
C. 1219. Prove that 9m (where m is a positive integer) can always be expressed as the sum of three positive square numbers.
(5 pont)
solution (in Hungarian), statistics
C. 1220. The diagram shows a regular rectangular lattice. The broken line can be continued in the same way as shown.
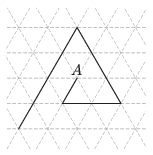
Every new line segment is one unit longer than the previous one. What is the minimum total length of the line to be drawn if the line is to end at a point whose distance from the starting point A is an integer?
(5 pont)
solution (in Hungarian), statistics
C. 1221. F is the midpoint of side AD of a square ABCD. N is the point lying closer to B that divides side AB in a 1:3 ratio. In what ratio does the circumscribed circle of triangle AFN divide the diagonal AC?
(5 pont)
solution (in Hungarian), statistics
C. 1222. The sum of the first four terms of a geometric progression is 15.6, and the sum of their reciprocals is 12.48. What are these four numbers if the first term is 0.1?
(5 pont)
solution (in Hungarian), statistics
C. 1223. The lateral faces of a regular four-sided pyramid are equilateral triangles. What is the angle enclosed by adjacent lateral faces?
(5 pont)
 |
Problems with sign 'B'Deadline expired on April 10, 2014. |
B. 4612. Each member of a group of 9 people sends happy new year cards to exactly k others. What may be the least possible value of k such that we can be certain that there is a pair of members who mutually greet each other?
(3 pont)
solution (in Hungarian), statistics
B. 4613. The rhombus A1B1C1D1 lies in the interior of a parallelogram ABCD. The vectors and
have the same direction, and the vectors
and
also have the same direction. Show that ABCD is a rhombus if and only if the sum of the areas of quadrilaterals AA1D1D and BCC1D1 is equal to the sum of the areas of quadrilaterals ABB1A1 and CDD1C1.
(Problem by L. Longáver, Matlap, Kolozsvár)
(3 pont)
solution (in Hungarian), statistics
B. 4614. Let x1,...,xn and y1,...,yn be nondecreasing sequences of non-negative numbers, such that the sum of the n terms is 1. a) What is the maximum possible value of ? b) What is the maximum possible value of
?
(5 pont)
solution (in Hungarian), statistics
B. 4615. Each angle of the triangle ABC is smaller than 120o. The isogonal point of the triangle is P. Draw lines through point P parallel to the sides. The parallels intersect side AB at D and E, side BC at F and G, and side CA at H and I. Let K, L and M denote the isogonal points of triangles DEP, FGP, HIP, respectively. Show that triangle KLM is equilateral.
Suggested by: Sz. Miklós, Herceghalom
(5 pont)
solution (in Hungarian), statistics
B. 4616. For what values of n do the numbers leave pairwise different remainders when divided by n?
(4 pont)
solution (in Hungarian), statistics
B. 4617. What angle may the hypotenuse of a right-angled triangle enclose with the median drawn to one of the legs?
Javasolta: G. Holló, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 4618. The polygon has both an inscribed circle and a circumscribed circle. The centre of the inscribed circle is O, and the centre of the circle OAiAi+1 is Ci (
, and An+1=A1). Prove that C1,C2,...,Cn are concyclic.
(5 pont)
solution (in Hungarian), statistics
B. 4619. Solve the equation .
Suggested by B. Kovács, Szatmárnémeti
(5 pont)
solution (in Hungarian), statistics
B. 4620. Prove that for any numbers ,
.
(6 pont)
solution (in Hungarian), statistics
B. 4621. For a certain tetrahedron, there exists a sphere that touches all edges, and there exists another sphere that touches the three edges bounding one face and also the extensions of the other three edges. Show that there exists a sphere for each face that touches the three edges bounding that face and also the extensions of the other three edges.
(6 pont)
 |
Problems with sign 'A'Deadline expired on April 10, 2014. |
A. 611. Let n be a positive integer. Determine the smallest possible value of over all a monic polynomials p with degree n.
(5 pont)
A. 612. Is there infinitely many positive integers that can be represented neither as the sum nor as the difference of two perfect powers?
(5 pont)
A. 613. There is given a convex quadrilateral \(\displaystyle ABCD\). The points \(\displaystyle E\) and \(\displaystyle F\) lie on the line segment \(\displaystyle AB\), \(\displaystyle G\) and \(\displaystyle H\) lie on \(\displaystyle BC\), \(\displaystyle I\) and \(\displaystyle J\) lie on \(\displaystyle CD\), and \(\displaystyle K\) and \(\displaystyle L\) lie on \(\displaystyle DA\) in such a way that \(\displaystyle AE<AF<AB\), \(\displaystyle BG<BH<BC\), \(\displaystyle CI<CJ<CD\), and \(\displaystyle DK<DL<DA\). The line \(\displaystyle EJ\) meets \(\displaystyle GL\) and \(\displaystyle HK\) at \(\displaystyle P\) and \(\displaystyle S\), and \(\displaystyle FI\) meets \(\displaystyle GL\) and \(\displaystyle HK\) at \(\displaystyle Q\) and \(\displaystyle R\), respectively. The points \(\displaystyle P\) and \(\displaystyle R\) lie on the diagonal \(\displaystyle AC\) and the points \(\displaystyle Q\) and \(\displaystyle S\) lie on \(\displaystyle BD\) (see the first cover). Suppose that each of the quadrilaterals \(\displaystyle AEPL\), \(\displaystyle BGQF\) and \(\displaystyle CIRH\) has an inscribed circle.
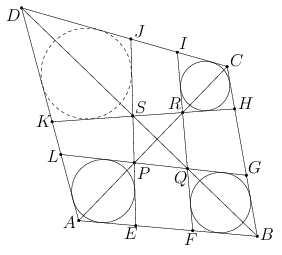
Show that the quadrilateral \(\displaystyle DKSJ\) also has an inscribed circle.
Based on a problem of the International Zhautykov Olympiad
(5 pont)
Upload your solutions above.
