Az A. 853. feladat (2023. április)

A. 853. Az általános helyzetű $\displaystyle A$, $\displaystyle B$, $\displaystyle C$, $\displaystyle A'$, $\displaystyle B'$, $\displaystyle C'$ pontokról tudjuk, hogy az $\displaystyle AA'$, $\displaystyle BB'$, $\displaystyle CC'$ egyenesek mind érintik ugyanazt az egyenlő szárú hiperbolát rendre az $\displaystyle A$, $\displaystyle B$ és $\displaystyle C$ pontokban, továbbá hogy az $\displaystyle A'B'C'$ háromszög körülírt köre megegyezik az $\displaystyle ABC$ háromszög Feuerbach-körével. Jelölje $\displaystyle s(A')$ az $\displaystyle A'$ pontnak az $\displaystyle ABC$ háromszög talpponti háromszögéhez tartozó Simson-egyenesét, $\displaystyle A^*$ pedig legyen az $\displaystyle A$-ból az $\displaystyle s(A')$-re állított merőlegesnek és a $\displaystyle B'C'$ egyenesnek a metszéspontja. Hasonlóan definiáljuk a $\displaystyle B^*$ és $\displaystyle C^*$ pontokat. Mutassuk meg, hogy az $\displaystyle A^*$, $\displaystyle B^*$ és $\displaystyle C^*$ pontok egy egyenesen vannak.

Javasolta: Bán-Szabó Áron (Budapest)

(7 pont)

A beküldési határidő 2023. május 10-én LEJÁRT.

Kezdjük két lemma belátásával:

1. Lemma: Legyen $\displaystyle ABC$ egy háromszög (nem a feladatbeli) és $\displaystyle P$ egy pont a körülírt körén. Ekkor $\displaystyle P$ izogonális konjugáltja a $\displaystyle P$ pont Simson-egyenesére merőleges ideális pont.

Legyen $\displaystyle X$ egy pont a síkon, és jelölje $\displaystyle X_a,X_b,X_c$ az $\displaystyle X$ pont tükörképeit rendre az $\displaystyle a,b,c$ oldalegyenesekre. Ismert, hogy ekkor az $\displaystyle (X_aX_bX_c)$ kör középpontja éppen $\displaystyle X$-nek az izogonális konjugáltja lesz. Vázlatos indoklás: ha $\displaystyle Y$ az $\displaystyle X$ izogonális konjugáltja, akkor könnyen láthatóan rajta van pl. az $\displaystyle X_cAX_b$ szögfelezőjén, és mivel a tükrözések miatt $\displaystyle X_cA=XA=X_bA$, ezért a szögfelező éppen az $\displaystyle X_bX_c$ felezőmerőlegese. Ha az $\displaystyle (X_aX_bX_c)$ kör létezik a szokásos kör formájában, akkor a középpontja is egy pont az Euklideszi síkon. Így $\displaystyle Y$ pontosan akkor lesz ideális pont, ha az $\displaystyle (X_aX_bX_c)$ kör egyenessé fajul. Viszont ismert, hogy egy pont vetületei a háromszög oldalegyeneseire pontosan akkor lesznek egy egyenesen, ha rajta van a körülírt körön (Simson-egyenes). Persze az $\displaystyle X_aX_bX_c$ háromszög az $\displaystyle X$ pont talpponti háromszögének kétszeres nagyítása $\displaystyle X$-ből, így az $\displaystyle X_aX_bX_c$ pontosan akkor fajul egyenessé, ha $\displaystyle X$ rajta van a körülírt körön. Továbbá vegyük észre, hogy ekkor az $\displaystyle X_bX_c,X_cX_a,X_aX_b$ szakaszok felezőmerőlegesei Simson-egyenesre merőleges egyenesekké fajulnak, azaz a metszéspontjuk ($\displaystyle Y$) valóban a Simson-egyenesre merőleges ideális pont lesz.

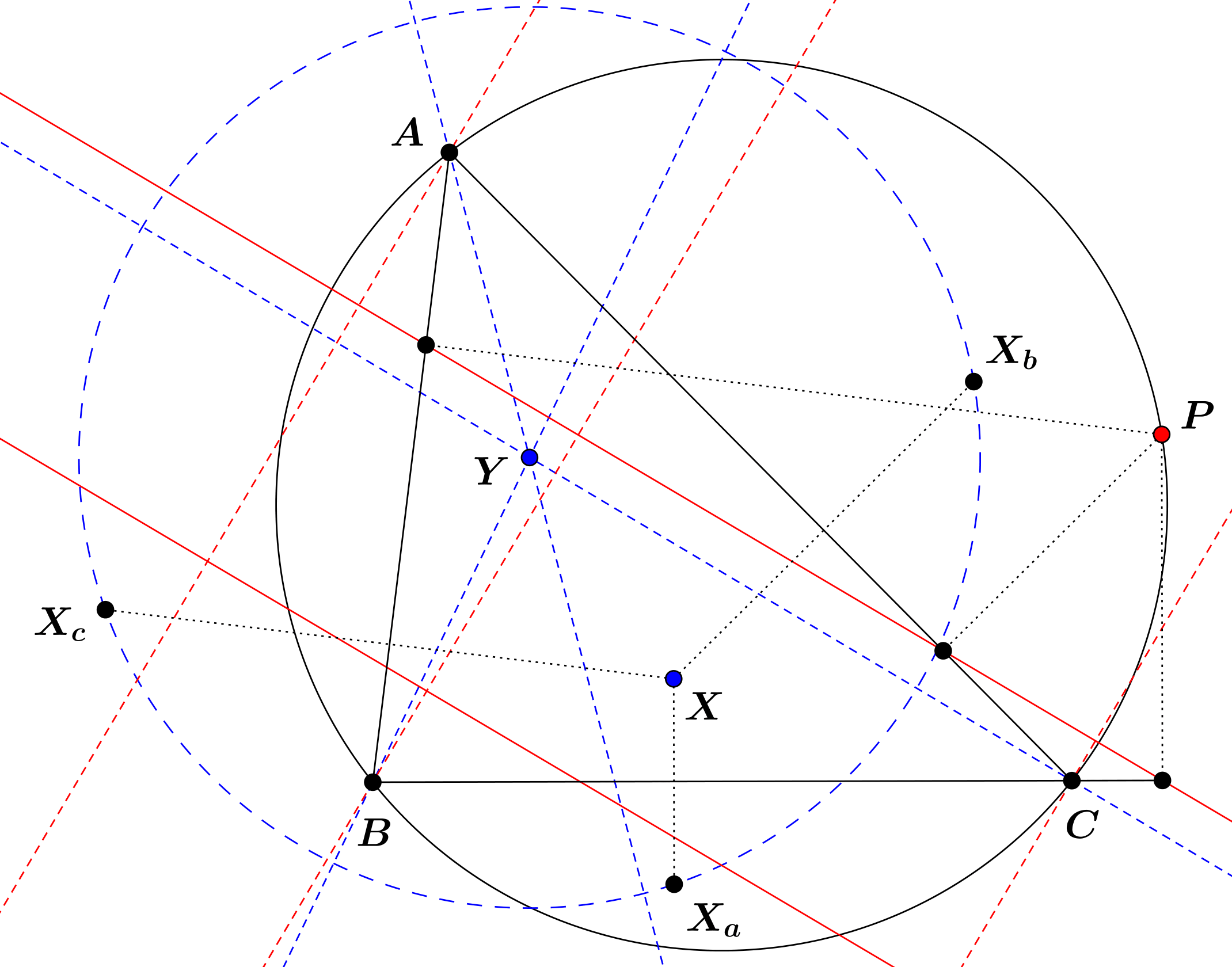
Térjünk vissza az eredeti feladat jelöléseihez. Legyen $\displaystyle \mathcal{H}$ a hiperbola, $\displaystyle DEF$ pedig az $\displaystyle ABC$ talpponti háromszöge.

2. Lemma: Ha $\displaystyle P,Q$ izogonális konjugáltak a $\displaystyle DEF$ háromszögben, akkor $\displaystyle Q$ rajta van $\displaystyle P$ polárisán ($\displaystyle \mathcal{H}$-ra nézve).

Legyen $\displaystyle H$ az $\displaystyle ABC$ háromszög magasságpontja. Ismert, hogy $\displaystyle H\in \mathcal{H}$, de most adunk egy másik bizonyítást: kevésbé ismert, hogy az $\displaystyle A,B,C$ pontokon átmenő kúpszeletek izogonális konjugáltjai egyenesek (itt az izogonális konjugálást az $\displaystyle ABC$ háromszögben értjük). Először is, ha egy pont egy egyenesen mozog, akkor a pontot az $\displaystyle A$ és a $\displaystyle B$ ponttal összekötve két perspektív sugársort kapunk. Most a mozgó pont izonális konjugáltját úgy kapjuk meg, hogy a két sugársornak a pontot kimetsző egyeneseit tükrözzük a megfelelő $\displaystyle A$ és $\displaystyle B$-beli szögfelezőkre. Így ismét két perspektív sugársort kapunk, és ismert, hogy két perspektív sugársor megfelelő egyeneseinek metszete kúpszelet. Ezen rajta vannak a háromszög csúcsai is, hiszen $\displaystyle A$ és $\displaystyle B$ a két sugársor középpontja, $\displaystyle C$-t pedig úgy kapjuk meg, hogy vesszük az egyenes és az $\displaystyle AB$ oldalegyenes metszéspontját. (Megjegyzés: ebből a korábbi állításra is adódik egy bizonyítás, hiszen az ideális pontokat $\displaystyle A$-val és $\displaystyle B$-vel összekötve a sugársorok még egybevágóak és azonos irányításúak is lesznek, és így a tükörképeikre is teljesül ez, és mivel nem az ideális egyenes lesz a tükörképek metszete, ezért csak kör lehet.)

Fordítva is teljesül a dolog: az $\displaystyle A$, $\displaystyle B$ és $\displaystyle C$ pontokon átmenő kúpszeleten futtatva egy pontot megint kaphatunk egy $\displaystyle A$ és egy $\displaystyle B$ ponton átmenő sugársort. Ha ismét tükrözzük az $\displaystyle A$ és a $\displaystyle B$-beli szögfelezőkre a megfelelő egyeneseket, akkor most két olyan perspektív sugársort kapunk, melyeknek van közös egyenese (a $\displaystyle C$ ponton átmenő sugarak tükörképe mindkét sugársornál az $\displaystyle AB$ egyenes), és ismert, hogy közös egyenessel rendelkező perspektív sugársorok megfelelő egyeneseinek metszete egyenes.

Mivel $\displaystyle \mathcal{H}$ egyenlő szárú, két ideális pontot tartalmaz, melyek merőlegesek. Mint láttuk, ezek izogonális konjugáltjai a körülírt körön lesznek, és mivel a sugársorok őket kimetsző két-két egyenese merőleges egymásra, ezért átellenes pontokat kapunk a körön. Így tehát $\displaystyle O$ rajta van a hiperbola izogonális konjugáltján, ekkor viszont $\displaystyle O$ izogonális konjugáltja, azaz a magasságpont rajta van a hiperbolán.

Jelölje ezután $\displaystyle t$ azt a transzformációt, amely minden $\displaystyle X\in PQ$ ponthoz az $\displaystyle A,B,C,H,X$ pontokon átmenő kúpszeletnek a $\displaystyle PQ$ egyenessel való második $\displaystyle X'$ metszéspontját rendeli hozzá. Nem nehéz belátni, hogy $\displaystyle t$ projektív (ez mindig igaz, nem csak egy háromszög három csúcsára és a magasságpontra).

Az $\displaystyle ABCHXX'$ hatszögre felírt Pascal-tétel miatt az $\displaystyle AB\cap HX,BC\cap XX',CH\cap X'A$ pontok egy egyenesen vannak. Vegyük észre, hogy $\displaystyle BC\cap XX'=BC\cap PQ=S$ egy fix pont. Így az $\displaystyle X\stackrel{H}{\mapsto}AB\cap HX=X_1$, $\displaystyle X_1\stackrel{S}{\mapsto} SX_1\cap CH=X_2$, $\displaystyle X_2\stackrel{A}{\mapsto}AX_2\cap PQ$ vetítések sorozata pont $\displaystyle X'$-t fogja eredményezni. Most nevezzük el a $\displaystyle PQ$ egyenesnek a $\displaystyle BC,AD,CA,BE,AB,CF$ egyenesekkel való metszéspontjait rendre $\displaystyle R_A,S_A,R_B,S_B,R_C,S_C$-nek. Mivel a $\displaystyle DEF$ háromszög beírt és hozzáírt köreinek középpontjai rendre $\displaystyle H,A,B,C$, a $\displaystyle DP,DQ$ egyenesek tükrösek a $\displaystyle DR_A,DS_A$ szögfelezőkre. Ez pont az jelenti, hogy a $\displaystyle PDQ$ szög két szögfelezője éppen $\displaystyle DR_A$ és $\displaystyle DS_A$, és ekkor ismert, hogy $\displaystyle (P,Q;R_A,S_A)=-1$ (egy lehetséges bizonyítás: felírjuk kétszer a szögfelezőtételt a $\displaystyle PQD$ háromszögre). Viszont $\displaystyle t:R_A\mapsto S_A$ (ilyenkor a kúpszelet a $\displaystyle DR_A\cup DS_A=BC\cup DA$ egyenespárrá fajul). Persze ugyanez elmondható az $\displaystyle R_B,R_C$ pontokról. Ám a $\displaystyle PQ$ egyenesen az $\displaystyle X\in PQ\mapsto X'\in PQ:(X,X';P,Q)=-1$ transzformáció ($\displaystyle P,Q$ pontokra való harmonikus konjugálás) is projektív, hiszen egy pont harmonikus társa vetítések sorozatával megkapható egy teljes négyes segítségével. Tehát a két projektív leképzés három pontban is megegyezik az egyenesen, azaz minden pontban. Így ha $\displaystyle R,S$ a két metszéspontja $\displaystyle \mathcal{H}$-nak $\displaystyle PQ$-val, akkor $\displaystyle (R,S;P,Q)=-1$, de ezt pont azt jelenti, hogy $\displaystyle Q$ rajta van $\displaystyle P$ polárisán.

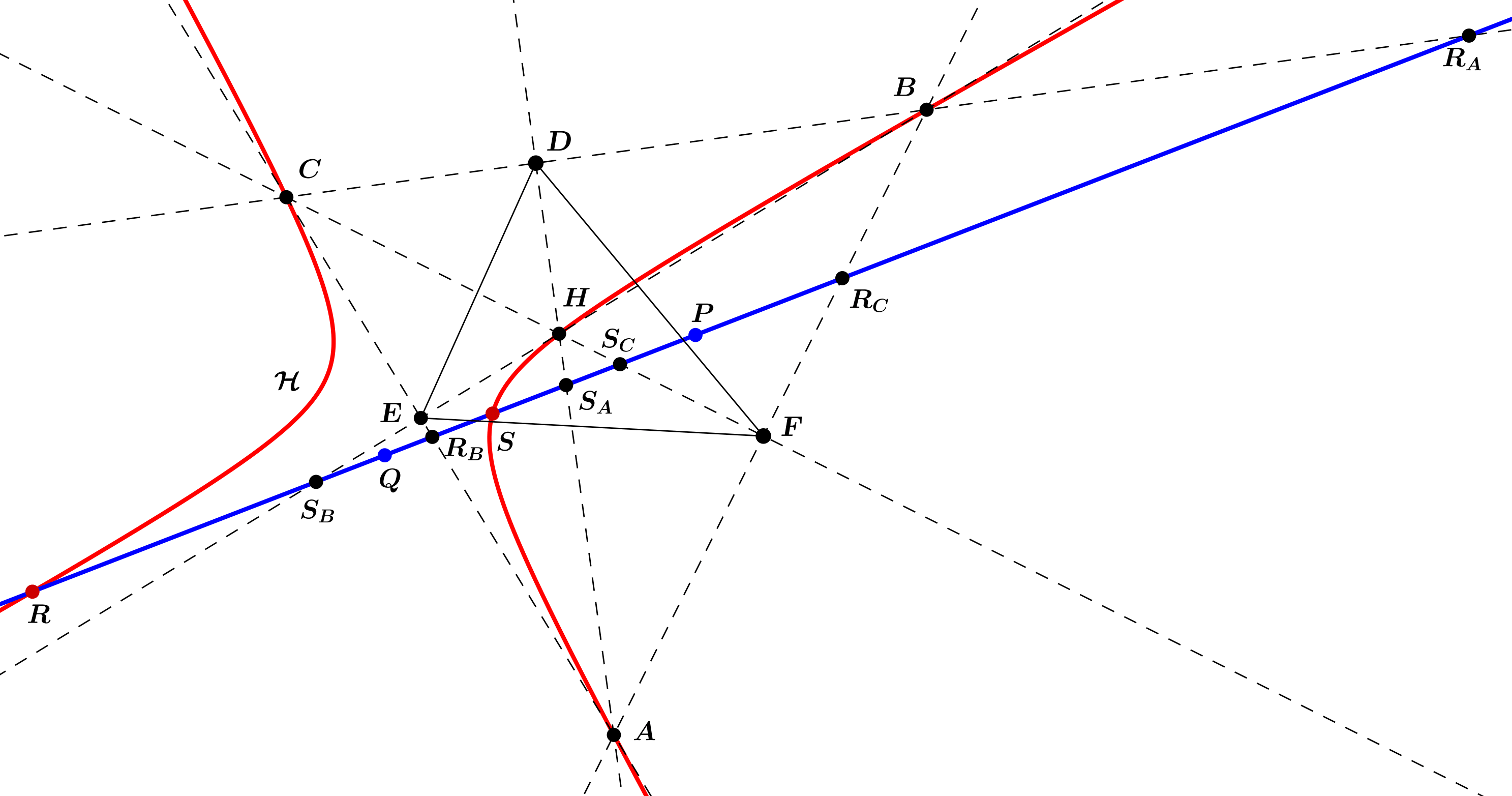
Most pedig belátjuk a bizonyítandó állítást. Jelölje $\displaystyle p(X)$ az $\displaystyle X$ pont polárisát $\displaystyle \mathcal{H}$-ra nézve.

Először is $\displaystyle A\in p(A')$, hiszen $\displaystyle AA'$ érinti $\displaystyle \mathcal{H}$-t $\displaystyle A$-ban. Továbbá a 2. lemma miatt $\displaystyle A'$ izogonális konjugáltja (a $\displaystyle DEF$ talpponti háromszögben) is rajta van $\displaystyle p(A')$-n, viszont az 1. lemma miatt ez éppen az $\displaystyle s(A')$-re merőleges ideális pont. Azaz $\displaystyle p(A')$ pontosan az $\displaystyle A$-ból $\displaystyle s(A')$-re állított merőleges lesz. Ugyanez elmondható persze $\displaystyle p(B')$-ről és $\displaystyle p(C')$-ről is. A következő állítás már tetszőleges kúpszeletre és nem egy egyenesre eső $\displaystyle A'$, $\displaystyle B'$, $\displaystyle C'$ pontra igaz, és ezt nyilván elég belátni a bizonyítás befejezéséhez:

3. Lemma: Tetszőleges kúpszelet és $\displaystyle A'$, $\displaystyle B'$, $\displaystyle C'$ pontok esetén legyen $\displaystyle A^*$ az $\displaystyle A'$ pont polárisának és a $\displaystyle B'C'$ egyenesnek a metszéspontja. $\displaystyle B^*$ és $\displaystyle C^*$ hasonló módon van definiálva. Bizonyítandó, hogy $\displaystyle A^*$, $\displaystyle B^*$ és $\displaystyle C^*$ egy egyenesre esnek. Vagy egyszerűbben fogalmazva: egy háromszög és a csúcsainak a polárisai által alkotott háromszög perspektív egymással.

Legyen $\displaystyle p(B')$ metszéspontja az $\displaystyle A'B'$ és $\displaystyle B'C'$ egyenesekkel rendre $\displaystyle M$ és $\displaystyle N$. Vetítsünk a $\displaystyle B^*$ ponton keresztül az $\displaystyle A'B'$ egyenesről a $\displaystyle B'C'$ egyenesre. Ekkor az $\displaystyle A'$ pont képe $\displaystyle C'$, az $\displaystyle M$ pont képen $\displaystyle N$, $\displaystyle B'$ képe pedig $\displaystyle B'$. Azt szeretnénk belátni, hogy $\displaystyle C^*$ képe $\displaystyle A^*$, ehhez pedig a vetítés kettősviszonytartása miatt azt kéne belátni, hogy $\displaystyle (A'MC^*B')=(C'NA^*B')$. Legyen az $\displaystyle A'B'$ pólusa a $\displaystyle K$ pont.

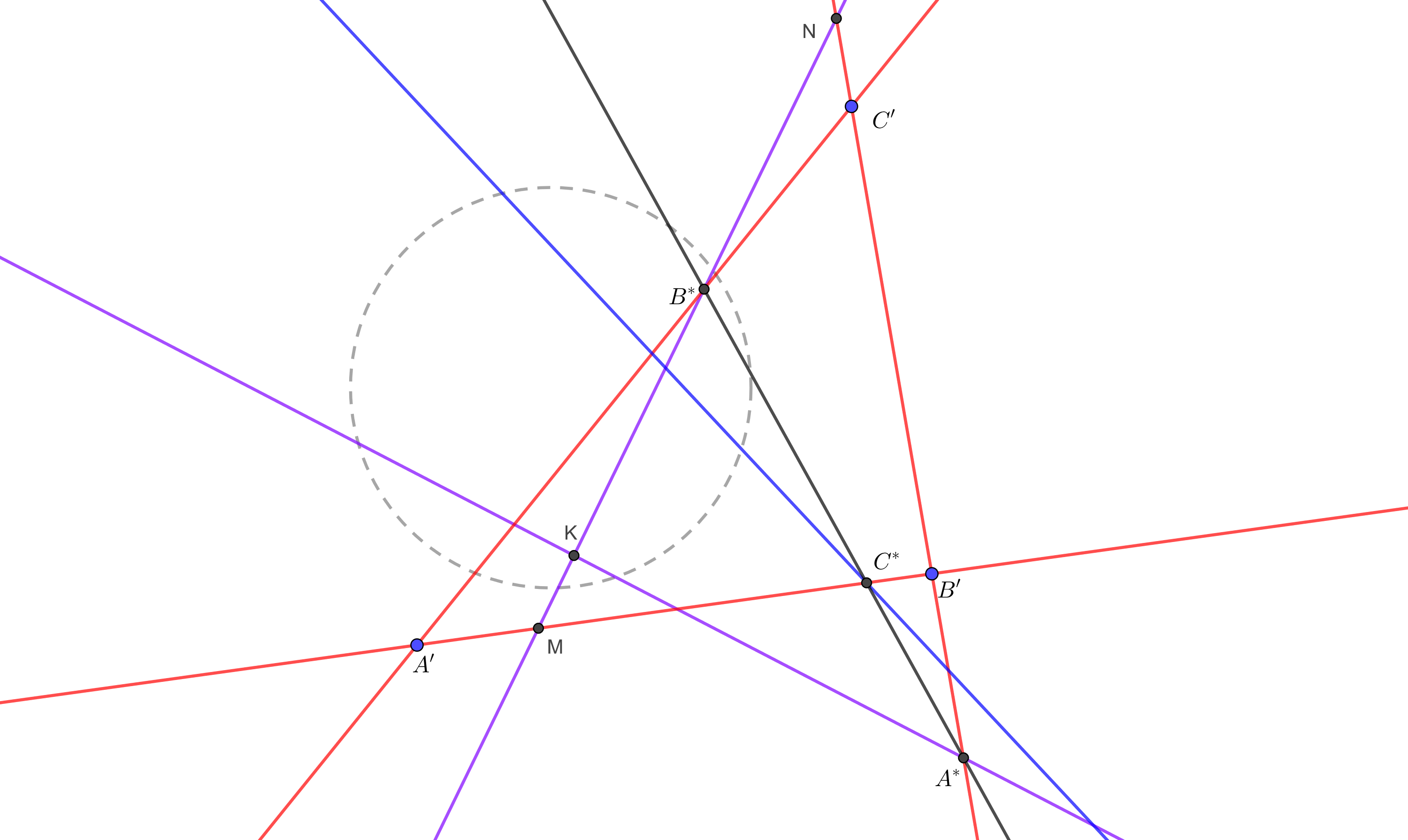
Ekkor La Hire miatt $\displaystyle M$ polárisa átmegy $\displaystyle K$-n ($\displaystyle M$ rajta van $\displaystyle A'B'$-n) és $\displaystyle B'$-n (hisz $\displaystyle M$ rajta van $\displaystyle p(B')$-n), $\displaystyle C^*$ polárisa szintén átmegy $\displaystyle K$-n ($\displaystyle C^*$ rajta van $\displaystyle A'B'$-n) és $\displaystyle C'$-n (hisz $\displaystyle C^*$ rajta van $\displaystyle p(C')$-n). Felhasználva, hogy a pólus-poláris hozzárendelés kettősviszonytartó, $\displaystyle (A'MC^*B')$ megegyezik a $\displaystyle p(A')=KA^*$, $\displaystyle p(M)=KB'$, $\displaystyle p(C^*)=KC'$, $\displaystyle p(B')=KB^*=KN$ egyenesek kettősviszonyával, ami pedig egyenlő az $\displaystyle (A^*B'C'N)$ kettősviszonnyal. Végül a kettősviszonyra vonatkozó jól ismert azonosságokból következik, hogy $\displaystyle (A^*B'C'N)=(C'NA^*B')$, és így készen vagyunk.

Statisztika:

2 dolgozat érkezett.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2023. áprilisi matematika feladatai