 |
Az A. 915. feladat (2025. október) |
A. 915. Adott egy kör és rajta az \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) pontok, melyek nem alkotnak egyenlő szárú háromszöget. A kör minden \(\displaystyle P\notin \{A,B,C\}\) pontjára jelölje \(\displaystyle A_P\), \(\displaystyle B_P\) és \(\displaystyle C_P\) rendre a kör \(\displaystyle P\)-beli érintőjének és az \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\)-beli érintőknek metszéspontjait. Bizonyítsuk be, hogy pontosan három olyan \(\displaystyle P\notin \{A,B,C\}\) pont van a körön, amelyre az \(\displaystyle A_P\), \(\displaystyle B_P\), \(\displaystyle C_P\) pontok léteznek, és az \(\displaystyle A_P\)-ből \(\displaystyle BC\)-re, \(\displaystyle B_P\)-ből \(\displaystyle CA\)-ra és \(\displaystyle C_P\)-ből \(\displaystyle AB\)-re állított merőlegesek egy pontban találkoznak. Továbbá mutassuk meg, hogy ez a három \(\displaystyle P\) pont egy szabályos háromszöget alkot.
Javasolta: Gyenes Zoltán Budapest)
(7 pont)
A beküldési határidő 2025. november 10-én LEJÁRT.
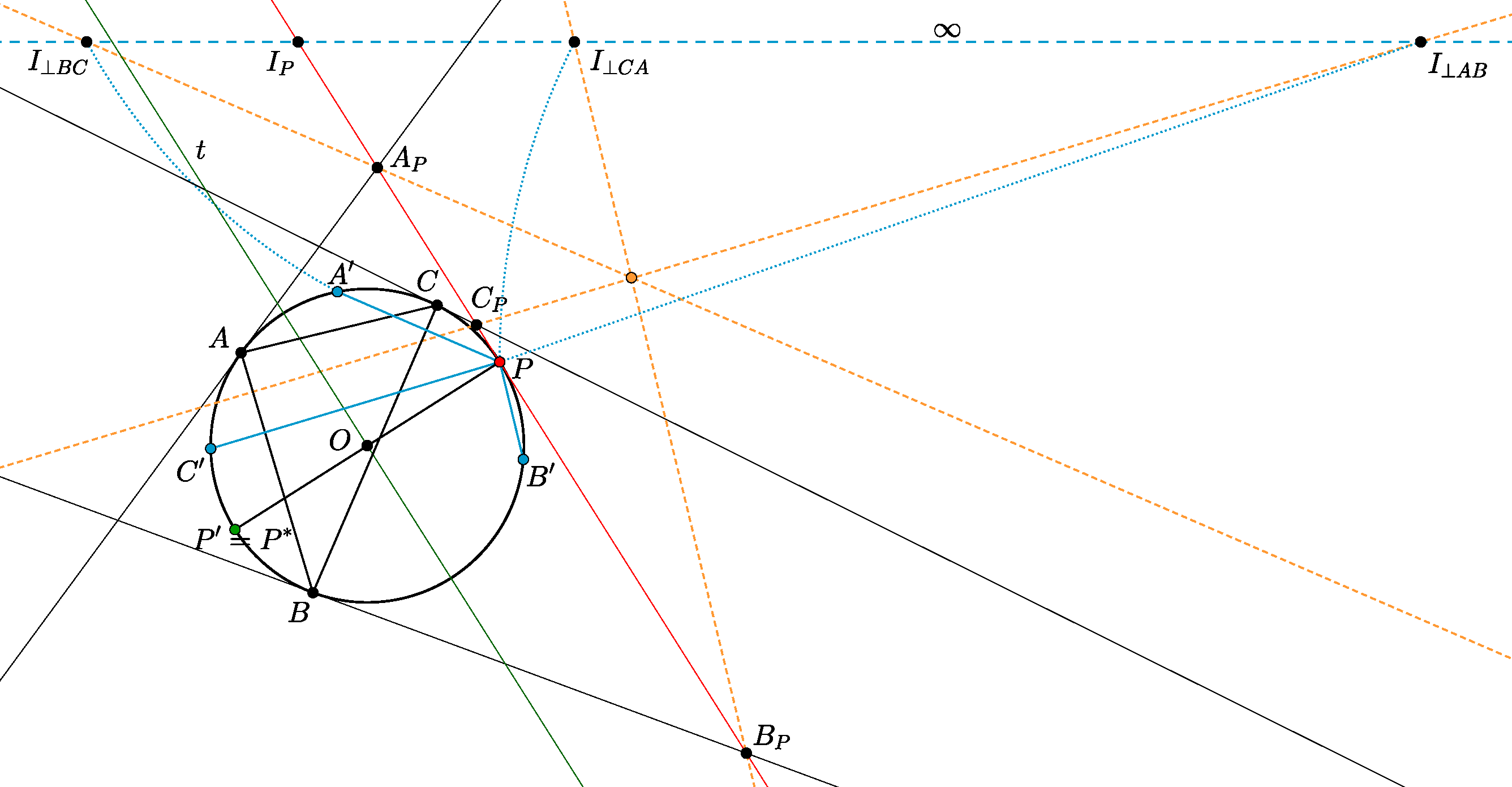
1. megoldás: Jelöljük a kör középpontját \(\displaystyle O\)-val. A projektív síkon fogunk dolgozni. Az ideális egyenest jelöljük a síkon vázlatosan \(\displaystyle \infty\)-vel. Legyen a \(\displaystyle P\)-beli érintő ideális pontja \(\displaystyle I_P\), továbbá legyenek az \(\displaystyle AB,BC,CA\) egyenesekre merőleges irányú ideális pontok rendre \(\displaystyle I_{\perp AB}, I_{\perp BC}, I_{\perp CA}\). Olyan \(\displaystyle P\) pontok érdekelnek minket, melyekre az \(\displaystyle A_PI_{\perp BC},B_PI_{\perp CA},C_PI_{\perp AB}\) egyenesek konkurensek. Ez ekvivalens azzal, hogy \(\displaystyle (A_P,B_P;C_P,I_P)=(I_{\perp BC},I_{\perp CA};I_{\perp AB},I_P)\). Vetítsük \(\displaystyle P\)-ből az \(\displaystyle (I_{\perp BC},I_{\perp CA};I_{\perp AB},I_P)\) pontnégyest: ha \(\displaystyle A',B',C'\) jelölik a \(\displaystyle P\)-ből \(\displaystyle BC,CA,AB\) egyenesekre állított merőlegeseknek a körrel vett második metszéspontjait, akkor azt kapjuk, hogy \(\displaystyle (I_{\perp BC},I_{\perp CA};I_{\perp AB},I_P)=(A',B';C',P)\) (hiszen a \(\displaystyle PI_P\) egyenes érinti a kört).
Vegyük észre, hogy az \(\displaystyle ABC,A'B'C'\) háromszögek egybevágóak. Sőt, egy tengelyes tükrözés viszi egymásba a két háromszöget, a tengely pedig az \(\displaystyle O\)-ból a \(\displaystyle P\) pont Simson-egyenesére állított merőleges, melyet \(\displaystyle t\)-vel jelölünk. (Ez például igazolható könnyű szögszámolással, felhasználva, hogy az \(\displaystyle AP\) egyenes \(\displaystyle A\)-izogonálisa, azaz a \(\displaystyle BAC\sphericalangle \) szögefelzőjére vett tükörképe merőleges a \(\displaystyle P\) pont Simson-egyenesére.)
Legyen most \(\displaystyle P'\) a \(\displaystyle P\) pont tükörképe \(\displaystyle t\)-re, \(\displaystyle P^*\) pedig \(\displaystyle P\) tükörképe \(\displaystyle O\)-ra, azaz a \(\displaystyle P\)-vel átellenes pont a körön. Visszatérve a feladatra, a \(\displaystyle t\)-re való tükrözésnek hála \(\displaystyle (A',B';C',P)=(A,B;C,P')\). Továbbá, a pólus-poláris transzformáció is kettősviszony-tartó, \(\displaystyle (A_P,B_P;C_P,I_P)=(PA,PB;PC,PO)\). A körre levetítve \(\displaystyle (PA,PB;PC,PO)=(A,B;C,P^*)\). Összesítve, az állítás, miszerint az \(\displaystyle A_P\)-ből \(\displaystyle BC\)-re, \(\displaystyle B_P\)-ből \(\displaystyle CA\)-ra és \(\displaystyle C_P\)-ből \(\displaystyle AB\)-re állított merőlegesek konkurensek, ekvivalens azzal, hogy \(\displaystyle (A,B;C,P')=(A,B;C,P^*)\), avagy \(\displaystyle P'=P^*\).
Be fogjuk látni, hogy pontosan három \(\displaystyle P\) pont esetén fog ez teljesülni, melyek egy szabályos háromszög három csúcsát alkotják. Vegyük fel \(\displaystyle P\)-t tetszőlegesen a körön. Mozgassuk el \(\displaystyle P\)-t a körön maradva \(\displaystyle x\) középponti szöggel. Ismert, hogy ekkor a Simson-egyenes, és így a \(\displaystyle t\) tengely is \(\displaystyle -\frac{x}{2}\)-el fordul el. A tükrözés miatt \(\displaystyle P'\) elfordulása \(\displaystyle -2x\). Mivel \(\displaystyle P^*\) csak \(\displaystyle P\) \(\displaystyle 180^{\circ}\)-os elforgatottja \(\displaystyle O\) körül, \(\displaystyle P^*\) is \(\displaystyle x\)-el fordul el. Így ha fix sebességgel mozgatjuk \(\displaystyle P\)-t a körön, \(\displaystyle P^*\) is így mozog, de \(\displaystyle P'\) kétszeres sebességgel fog mozogni ellentétes irányba. Ezért a két pont előbb-utóbb egybe fog esni. És miután egybeestek, mikor fog ismét megtörténni az egybeesés? Pont akkor, ha \(\displaystyle x+2x=3x\) többszöröse \(\displaystyle 360^{\circ}\)-nak, avagy \(\displaystyle x=\pm 120^{\circ}\). Ezzel beláttuk az állítást.
2. megoldás: A megoldásban komplex számokat fogunk használni. A feladatban szereplő körnek a \(\displaystyle |z|=1\) egységkört fogjuk választani. Először belátjuk, hogy ha \(\displaystyle z\neq w\) és \(\displaystyle |z|=|w|=1\), akkor ezekben a pontokban az egységkörhöz húzott érintők metszéspontja \(\displaystyle t=\frac{2zw}{z+w}\), azaz a két adott komplex szám harmonikus közepe. Ehhez csak azt kell belátnunk, hogy \(\displaystyle z\) és \(\displaystyle t-z\) merőleges egymásra, azaz \(\displaystyle \frac{z}{t-z}\) tisztán képzetes szám (logikai szimmetria miatt ekkor nyilván \(\displaystyle w\) és \(\displaystyle t-w\) is merőleges egymásra).
Először hozzuk a törtet egyszerűbb alakra:
\(\displaystyle \frac{z}{t-z}=\frac{z}{\frac{zw-z^2}{z+w}}=\frac{z+w}{w-z},\)
és ez nyilván tisztán képzetes, hiszen \(\displaystyle z+w\) és \(\displaystyle w-z\) merőleges egymásra \(\displaystyle |z|=|w|\) miatt.
Ezek után ha \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle c\) három adott pont az egységkörön, akkor a feladatban szereplő pontok \(\displaystyle a_p=\frac{2ap}{a+p}\), \(\displaystyle b_p=\frac{2bp}{b+p}\) és \(\displaystyle c_p=\frac{2cp}{c+p}\). Ezek után írjuk fel az \(\displaystyle A_P\) pontból a \(\displaystyle BC\) egyenesre állított merőleges egyenletét. A \(\displaystyle Z\) pont akkor van rajta ezen a merőlegesen, ha \(\displaystyle \frac{z-a_p}{b-c}\) tisztán képzetes, vagyis a konjugáltja egyenlő az ellentettjével:
\(\displaystyle \frac{z-a_p}{b-c}=-\frac{\overline{z}-\overline{a_p}}{\overline{b}-\overline{c}}. \)
Most egyszerűbb alakra hozhatjuk a jobb oldalon szereplő törtet, felhasználva, hogy \(\displaystyle |x|=1\) azt jelenti, hogy \(\displaystyle \overline{x}=\frac{1}{x}\): ehhez először is
\(\displaystyle \overline{a_p}=\frac{2\overline{a}\overline{p}}{\overline{a}+\overline{p}}=\frac{\frac{2}{ap}}{\frac{1}{a}+\frac{1}{p}}=\frac{2}{a+p}, \)
és így
\(\displaystyle \frac{\overline{z}-\overline{a_p}}{\overline{b}-\overline{c}}=\frac{\overline{z}-\frac{2}{a+p}}{\frac{1}{b}-\frac{1}{c}}=\frac{bc\overline{z}-\frac{2bc}{a+p}}{c-b}, \)
így végül a keresett egyenes egyenlete
\(\displaystyle z-\frac{2ap}{a+p}=bc\overline{z}-\frac{2bc}{a+p}. \)
Most kiszámíthatjuk az \(\displaystyle A_P\) pontból a \(\displaystyle BC\) egyenesre és a \(\displaystyle B_P\) pontból az \(\displaystyle AC\) egyenesre állított merőlegesek metszéspontját: a két merőleges egyenletét kivonva egymásból azt kapjuk, hogy
\(\displaystyle \frac{2bp}{b+p}-\frac{2ap}{a+p}=(bc-ac)\overline{z}-\frac{2bc}{a+p}+\frac{2ac}{b+p}, \)
vagyis
\(\displaystyle \frac{2(b-a)p^2}{(a+p)(b+p)}=c(b-a)\overline{z}+\frac{2(a^2-b^2)c+2(a-b)cp}{(a+p)(b+p)}, \)
ahonnan
\(\displaystyle \overline{z}=2\cdot\frac{p^2+(a+b+p)c}{c(a+p)(b+p)} \)
Így végül annak a feltétele, hogy a három merőleges egy ponton megy át, így alakul:
\(\displaystyle \frac{p^2+(a+b+p)c}{c(a+p)(b+p)}=\frac{p^2+(b+c+p)a}{a(b+p)(c+p)}, \)
ahonnan
\(\displaystyle a(c+p)\left(p^2+(a+b+p)c\right)=c(a+p)\left(p^2+(b+c+p)a\right), \)
és a szorzásokat elvégezve
\(\displaystyle ap^3+2acp^2+(a+b+c)acp+ac^2(a+b)=cp^3+2acp^2+(a+b+c)acp+a^2c(b+c), \)
és ez végül a \(\displaystyle p^3=abc\) egyenletté egyszerűsödik (\(\displaystyle p\neq -a,-b,-c\) esetén az átalakítások ekvivalensek voltak, mert nem kellett nullával osztanunk vagy szoroznunk). Ennek a három megoldása valóban szabályos háromszöget alkot. Azt kell még ellenőriznünk, hogy mikor eshet egybe ennek a megoldása \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle -a\), \(\displaystyle -b\) vagy \(\displaystyle -c\) valamelyikével: ha pl. \(\displaystyle a^3=abc\), akkor \(\displaystyle bc=a^2\), és ekkor egyenlő szárú a háromszög, hiszen ez azzal ekvivalens, hogy \(\displaystyle OA\) merőleges \(\displaystyle BC\)-re, ahol \(\displaystyle O\) az \(\displaystyle ABC\) háromszög körülírt körének középpontja. Sajnos a \(\displaystyle -a\)-val lehet egyenlő: ilyenkor \(\displaystyle a^2=-bc\), azaz \(\displaystyle OA\) párhuzamos \(\displaystyle BC\)-vel (vagy másképp a \(\displaystyle B\) és a \(\displaystyle C\) csúcsnál lévő szögek különbsége \(\displaystyle 90^\circ\)), ez kimaradt a feladat kikötései közül.
Statisztika:
26 dolgozat érkezett. 7 pontot kapott: Ali Richárd, Aravin Peter, Bodor Mátyás, Bolla Donát Andor, Bui Thuy-Trang Nikolett, Diaconescu Tashi, Ethan Y.Wang, Forrai Boldizsár, Gyenes Károly, Li Mingdao, Szakács Ábel, Tianyue DAI, Vigh 279 Zalán, Vincze Marcell, Vödrös Dániel László. 6 pontot kapott: Prohászka Bulcsú, Sárdinecz Dóra. 5 pontot kapott: 1 versenyző. 4 pontot kapott: 1 versenyző. 0 pontot kapott: 5 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2025. októberi matematika feladatai

