Az A. 922. feladat (2025. december)

A. 922. Rögzítsünk két pozitív egész számot, \(\displaystyle a\)-t és \(\displaystyle b\)-t. Legyen \(\displaystyle n\) egy pozitív egész szám, és \(\displaystyle T\) egy \(\displaystyle an\times bn\)-es tábla mezőinek egy fekete–fehér színezése, melyben van legalább két fehér mező. Csigusz, a csiga elindult egy fehér mezőről, bejárta az összes fehér mezőt pontosan egyszer, majd visszaért a kiinduló mezőjére, mindezt úgy, hogy végig csak oldalszomszédos fehér mezők között haladt. Ezután észrevette, hogy ezt pontosan egyféleképpen tudta megtenni (vagyis azután, hogy elindult, már csak egyféleképpen tudta befejezni a körutat).

Jelölje \(\displaystyle \mathcal{T}_n\) azon \(\displaystyle T\) színezések halmazát, melyekre teljesül a fenti tulajdonság, és jelölje \(\displaystyle \phi(T)\) a fehér mezők számát \(\displaystyle T\)-ben. Mutassuk meg, hogy

\(\displaystyle L=\lim_{n\to \infty} \dfrac{\max_{T\in \mathcal{T}_n} \phi(T)}{abn^2} \)

létezik minden pozitív egész \(\displaystyle a\) és \(\displaystyle b\) esetén, és határozzuk meg \(\displaystyle L\) értékét.

Javasolta: Lovas Márton és Beke Csongor (Cambridge)

(7 pont)

A beküldési határidő 2026. január 12-én LEJÁRT.

Megmutatjuk, hogy \(\displaystyle L\) értéke minden \(\displaystyle a,b\geq 1\) mellett létezik, és \(\displaystyle L=1\).

Először vizsgáljuk az \(\displaystyle a=1\), \(\displaystyle b=1\) esetet, tehát a táblánk négyzet alakú. Mutatunk egy konstrukciót \(\displaystyle n = 4k+7\)-re, ahol \(\displaystyle k\in \mathbb{N}\).

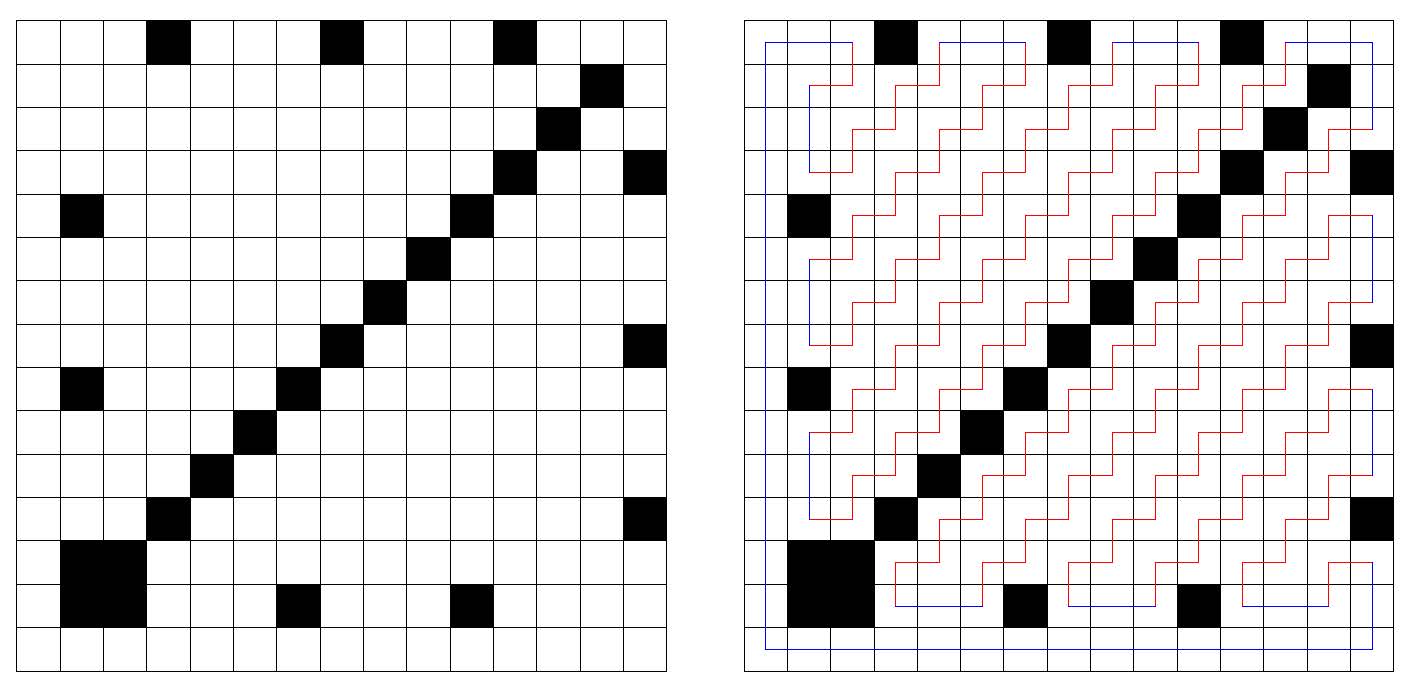
Megmutatjuk, hogy \(\displaystyle k=2\) esetén ez a kitöltés megfelelő. Tetszőleges tábla, és néhány, már berajzolt útvonalrészlet esetén hívjuk használtnak azokat a mezőket, melyek vagy feketék, vagy fehérek, és már két berajzolt (mezők közt haladó) útvonal részlet is érinti az adott mezőt.

Ekkor vegyük észre, hogy ha egy fehér mező két használt mezővel is szomszédos, akkor egyértelműen meghatározható, hogy Csigusz mely vele szomszédos két mezőről és mezőre lép oda és onnan.

Ennek megfelelően a baloldali, üres táblában egyértelműen meghatározhatóak a jobboldali táblán látható piros útvonalrészletek (a mellékátló felett és alatt két használt szomszédja van a fehér mezőknek, mely új használt mezőket eredményez, és így tovább).

Könnyű látni, hogy innen a befejezés egyértelmű (hiszen az útvonalnak egyetlen, önmagába záródó körnek kell lennie), és létezik, ez az ábrán kékkel vannak jelölve. Hasonló konstrukció működik bármely \(\displaystyle k\in \mathbb{N}\) esetén.

A fehér mezők száma

\(\displaystyle \phi(T_{k}) = (7+4k)^2 - (4 + (4k+3) + 2k + 2(k+1)) = n^2 - l(n) \)

ahol \(\displaystyle l\) lineáris függvénye \(\displaystyle n=4k+7\)-nek. Ha egy \(\displaystyle 4k+7\) méretű konstrukció köré fentről és a jobbról egy, kettő vagy három fekete sávot rakunk, akkor kapunk egy konstrukciót \(\displaystyle 4k+8\), \(\displaystyle 4k+9\) illetve \(\displaystyle 4k+10\)-re, vagyis minden kellően nagy \(\displaystyle n\) esetén

\(\displaystyle \max_{T\in \mathcal{T}_n} \phi(T) \geq n^2-l(n)-6n. \)

Tehát a keresett határérték valóban létezik, és

\(\displaystyle \lim_{n\to \infty} \frac{\max_{T\in \mathcal{T}_n} \phi(T)}{n^2} \geq \lim_{n\to \infty} \frac{n^2-l(n)-6n}{n^2}=1-\lim_{n\to \infty} \frac{l(n)+6n}{n^2} = 1. \)

Mivel \(\displaystyle \phi(T)\leq n^2\), az \(\displaystyle a=1\), \(\displaystyle b=1\) esetben \(\displaystyle L=1\).

Az általános konstrukcióhoz először módosítjuk a négyzet alakú táblát, amit találtunk: a bal alsó sarkot változtassuk fekete mezővé, vegyük az egész táblát körbe minden oldalról egy fekete sávval, viszont a fekete sávban legyen két lyuk (fehér mező), éppen az eredeti bal alsó sarokkal szomszédosan (ezt a két mezőt jelölje \(\displaystyle A\) és \(\displaystyle B\)).

Így kapunk egy táblát, melyben pontosan egyféleképpen lehet minden fehér mezőt érintve \(\displaystyle A\)-ból \(\displaystyle B\)-be jutni. Parkettázzunk ki egy \(\displaystyle a\times b\) méretű négyzetrácsot ilyen táblákkal, köztük \(\displaystyle m\) vastagságú fekete mezőkkel az ábra szerint (az \(\displaystyle a=3\), \(\displaystyle b=4\) esetben).

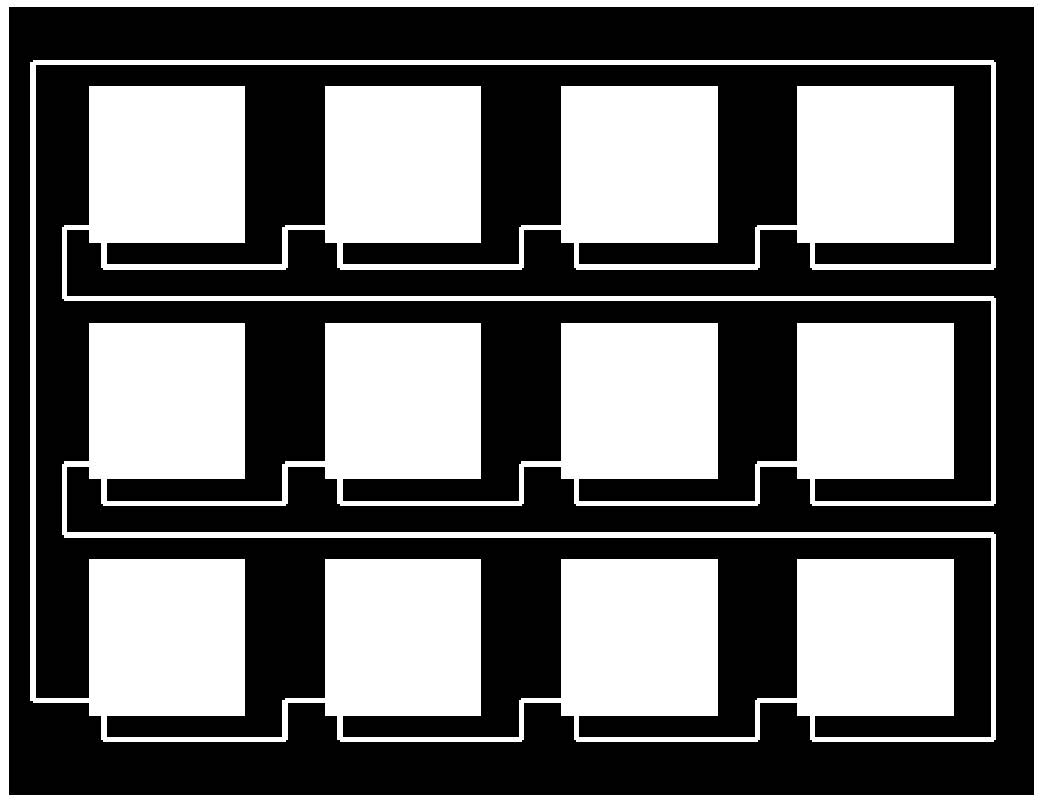
Végül fúrjunk alagutakat a fekete sávokba, ezzel sorosan összekötve a táblák szélső két mezőjét az ábra szerint. Világos, hogy például \(\displaystyle m=10\) esetén ezt már biztosan meg lehet tenni. Csigusz kénytelen az összes táblát érinteni, hiszen mindegyik tartalmaz fehér mezőt, és ezt csak egyféleképpen teheti meg. A konstrukció tetszőleges \(\displaystyle a\) és \(\displaystyle b\) értékek mellett hasonlóan működik.

Így egy adott \(\displaystyle n\times n\)-es táblából készítettünk egy megfelelő \(\displaystyle [(n+m)\cdot a + m]\times [(n+m)\cdot b+m]\) méretű táblát. Ennek az oldalarányai még éppen nem felelnek meg, viszont \(\displaystyle n\)-től függetlenül, legfeljebb \(\displaystyle a+b\) fekete sávot az új tábla jobb vagy felső oldalára illesztve kapunk egy konstrukciót, melyben a fekete mezők száma legfeljebb \(\displaystyle abl(n) + (a+b)g(n)\), ahol \(\displaystyle l\) és \(\displaystyle g\) lineáris függvényei \(\displaystyle n\)-nek (az összegbe a négyzetre készített konstrukcióból származó, és köztük beékelt, legfeljebb \(\displaystyle m\leq 10\) vastagságú fekete sávokat számoltuk bele, illetve azokat, melyeket jobbra és felülre helyeztünk), így ebben az esetben is \(\displaystyle L\) létezik és \(\displaystyle L=1\).

Statisztika:

Az A. 922. feladat értékelése még nem fejeződött be.

A KöMaL 2025. decemberi matematika feladatai