 |
A B. 4125. feladat (2008. november) |
B. 4125. Egy 45o-os szögtartomány belsejében adott két pont. Szerkesszünk olyan egyenlő szárú háromszöget, amelynek alapja a szög egyik szárán, harmadik csúcsa a másik szárán van, és a két pont illeszkedik a háromszög egy-egy oldalára.
(4 pont)
A beküldési határidő 2008. december 15-én LEJÁRT.
Megoldás: Tegyük fel, hogy az ABC egyenlőszárú háromszög AB alapja az a szögszárra esik, a P és Q pontok pedig az AC, illetve BC szárak belső pontjai az ábrán látható módon. Tükrözzük a Q pontot a b szárra. Ha az ACB szög nagysága 2
, akkor a PCO szög 45o-, az OCQ szöggel egyenlő OCQ' szög pedig 45o+, vagyis a PCQ' szög derékszög, a PQ' szakasz pedig elválasztja egymástól az O és C pontokat.
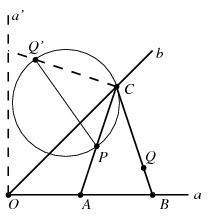
Ezek alapján a C csúcsot a következőképpen szerkeszthetjük meg. Válasszuk ki az egyik szögszárat (a). Ha a két adott pontot összekötő egyenes merőleges erre, akkor nincs olyan háromszög amelynek az alapja erre az egyenesre esne (a szerkesztéssel elfajuló háromszöget kapnánk). Ellenkező esetben válasszuk ki azt a pontot (Q), amelynek a-ra eső merőleges vetülete távolabb esik az adott szögtartomány O csúcsától. Kössük össze az így kapott Q' tükörképet a másik ponttal (P), majd szerkesszük meg a PQ' szakasz Thalész körét. Tekintsük ennek azt a felét, amelyet a PQ' egyenes O-tól elválaszt, ennek a másik szögszárral (b) alkotott egyetlen metszéspontja lesz a háromszög C csúcsa. A háromszög másik két csúcsát a CP, illetve CQ egyeneseknek a-val alkotott metszéspontjaként nyerjük. Könnyen meggondolhatjuk, hogy ez a szerkesztési eljárás valóban a feladat megoldását szolgáltatja. Mivel az a szögszár kiválasztása tetszés szerint történhet, a feladatnak egyetlen megoldása van, ha az adott két pontot összekötő egyenes merőleges valamelyik szögszárra, minden más esetben pedig két megoldás lesz.
Statisztika:
61 dolgozat érkezett. 4 pontot kapott: Ágoston Tamás, Aujeszky Tamás, Bálint Dániel, Blázsik Zoltán, Botos Csongor, Böőr Katalin, Cséke Balázs, Csere Kálmán, Damásdi Gábor, Dinh Hoangthanh Attila, Éles András, Énekes Péter, Fonyó Dávid, Frankl Nóra, Győrfi 946 Mónika, Huszár Kristóf, Janzer Olivér, Keresztfalvi Tibor, Kiss 716 Eszter, Kiss 902 Melinda Flóra, Klenk 191 Blanka, Korondi Zénó, Kovács 235 Gábor, Lajos Mátyás, Lovas Lia Izabella, Márkus Bence, Németh Bence, Nguyen Milán, Rábai Domonkos, Ratku Antal, Somogyi Ákos, Szabó 928 Attila, Szenczi Zoltán, Tóth 222 Barnabás, Tóth Tekla, Tubak Dániel, Varga 171 László, Weisz Gellért. 3 pontot kapott: Nagy 729 Krisztina, Szalai Zsófia, Weisz Ágoston. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 14 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2008. novemberi matematika feladatai